Το νέο Breakthrough φέρνει τον πολλαπλασιασμό μήτρας πιο κοντά στο ιδανικό | Περιοδικό Quanta

Οι επιστήμονες υπολογιστών είναι μια απαιτητική ομάδα. Για αυτούς, δεν αρκεί να λάβουν τη σωστή απάντηση σε ένα πρόβλημα — ο στόχος, σχεδόν πάντα, είναι να λάβουν την απάντηση όσο το δυνατόν πιο αποτελεσματικά.

Πάρτε την πράξη του πολλαπλασιασμού πινάκων ή πινάκων αριθμών. Το 1812, ο Γάλλος μαθηματικός Jacques Philippe Marie Binet σκέφτηκε τους βασικούς κανόνες που εξακολουθούμε να διδάσκουμε στους μαθητές. Λειτουργεί τέλεια, αλλά άλλοι μαθηματικοί έχουν βρει τρόπους να απλοποιήσουν και να επιταχύνουν τη διαδικασία. Τώρα το καθήκον του επιτάχυνση της διαδικασίας Ο πολλαπλασιασμός πινάκων βρίσκεται στη διασταύρωση των μαθηματικών και της επιστήμης των υπολογιστών, όπου οι ερευνητές συνεχίζουν να βελτιώνουν τη διαδικασία μέχρι σήμερα — αν και τις τελευταίες δεκαετίες τα κέρδη ήταν σχετικά μέτρια. Από το 1987, οι αριθμητικές βελτιώσεις στον πολλαπλασιασμό πίνακα ήταν «μικρές και ... εξαιρετικά δύσκολο να επιτευχθούν», είπε. Φρανσουά Λε Γκαλ, επιστήμονας υπολογιστών στο Πανεπιστήμιο της Ναγκόγια.

Τώρα, τρεις ερευνητές - ο Ran Duan και ο Renfei Zhou του Πανεπιστημίου Tsinghua και ο Hongxun Wu του Πανεπιστημίου της Καλιφόρνια στο Μπέρκλεϋ - έχουν κάνει ένα σημαντικό βήμα προς τα εμπρός για να επιτεθούν σε αυτό το πολυετές πρόβλημα. Δικα τους νέα αποτελέσματα, που παρουσιάστηκε τον περασμένο Νοέμβριο στο συνέδριο Foundations of Computer Science, προέρχονται από μια απροσδόκητη νέα τεχνική, είπε ο Le Gall. Αν και η ίδια η βελτίωση ήταν σχετικά μικρή, ο Le Gall την αποκάλεσε «εννοιολογικά μεγαλύτερη από άλλες προηγούμενες».

Η τεχνική αποκαλύπτει μια προηγουμένως άγνωστη και ως εκ τούτου αναξιοποίητη πηγή πιθανών βελτιώσεων και έχει ήδη αποδώσει καρπούς: Ένα δεύτερο χαρτί, που δημοσιεύτηκε τον Ιανουάριο, βασίζεται στην πρώτη για να δείξει πώς μπορεί να ενισχυθεί ακόμη περισσότερο ο πολλαπλασιασμός πινάκων.

«Πρόκειται για μια σημαντική τεχνική ανακάλυψη», είπε William Kuszmaul, θεωρητικός επιστήμονας υπολογιστών στο Πανεπιστήμιο του Χάρβαρντ. «Είναι η μεγαλύτερη βελτίωση στον πολλαπλασιασμό μήτρας που έχουμε δει εδώ και πάνω από μια δεκαετία».

Εισαγάγετε το Matrix

Μπορεί να φαίνεται σαν ένα ασαφές πρόβλημα, αλλά ο πολλαπλασιασμός πίνακα είναι μια θεμελιώδης υπολογιστική πράξη. Είναι ενσωματωμένο σε ένα μεγάλο ποσοστό των αλγορίθμων που χρησιμοποιούν οι άνθρωποι καθημερινά για μια ποικιλία εργασιών, από την εμφάνιση πιο ευκρινών γραφικών υπολογιστή έως την επίλυση υλικοτεχνικών προβλημάτων στη θεωρία δικτύου. Και όπως και σε άλλους τομείς υπολογισμού, η ταχύτητα είναι πρωταρχικής σημασίας. Ακόμη και μικρές βελτιώσεις θα μπορούσαν τελικά να οδηγήσουν σε σημαντική εξοικονόμηση χρόνου, υπολογιστικής ισχύος και χρημάτων. Αλλά προς το παρόν, οι θεωρητικοί ενδιαφέρονται κυρίως να καταλάβουν πόσο γρήγορη μπορεί να είναι ποτέ η διαδικασία.

Ο παραδοσιακός τρόπος πολλαπλασιασμού δύο n-με-n πίνακες — πολλαπλασιάζοντας αριθμούς από κάθε γραμμή στον πρώτο πίνακα με αριθμούς στις στήλες του δεύτερου — απαιτεί n³ χωριστούς πολλαπλασιασμούς. Για πίνακες 2 επί 2, αυτό σημαίνει 2³ ή 8 πολλαπλασιασμούς.

Το 1969, ο μαθηματικός Volker Strassen αποκάλυψε μια πιο περίπλοκη διαδικασία που μπορούσε να πολλαπλασιάσει 2 επί 2 πίνακες σε μόλις επτά πολλαπλασιαστικά βήματα και 18 προσθήκες. Δύο χρόνια αργότερα, ο επιστήμονας υπολογιστών Shmuel Winograd έδειξε ότι το επτά είναι, πράγματι, το απόλυτο ελάχιστο για πίνακες 2 προς 2.

Ο Strassen εκμεταλλεύτηκε την ίδια ιδέα για να δείξει ότι όλα είναι μεγαλύτερα n-με-n Οι πίνακες μπορούν επίσης να πολλαπλασιαστούν σε λιγότερα από n³ βήματα. Ένα βασικό στοιχείο σε αυτή τη στρατηγική περιλαμβάνει μια διαδικασία που ονομάζεται αποσύνθεση - η διάσπαση ενός μεγάλου πίνακα σε διαδοχικά μικρότερες υπομήτρες, οι οποίες μπορεί να καταλήξουν να είναι τόσο μικρές όσο 2-από-2 ή ακόμα και 1-από-1 (αυτοί είναι απλώς απλοί αριθμοί).

Το σκεπτικό για τη διαίρεση μιας τεράστιας συστοιχίας σε μικροσκοπικά κομμάτια είναι αρκετά απλή, σύμφωνα με Βιρτζίνια Βασιλέβσκα Γουίλιαμς, επιστήμονας υπολογιστών στο Ινστιτούτο Τεχνολογίας της Μασαχουσέτης και συν-συγγραφέας μιας από τις νέες εργασίες. «Είναι δύσκολο για έναν άνθρωπο να κοιτάξει σε μια μεγάλη μήτρα (ας πούμε, της τάξης των 100 επί 100) και να σκεφτεί τον καλύτερο δυνατό αλγόριθμο», είπε η Vassilevska Williams. Ακόμη και οι πίνακες 3 προς 3 δεν έχουν λυθεί πλήρως ακόμη. "Παρ' όλα αυτά, μπορεί κανείς να χρησιμοποιήσει έναν γρήγορο αλγόριθμο που έχει ήδη αναπτύξει για μικρούς πίνακες για να αποκτήσει επίσης έναν γρήγορο αλγόριθμο για μεγαλύτερους πίνακες."

Το κλειδί για την ταχύτητα, έχουν καθορίσει οι ερευνητές, είναι η μείωση του αριθμού των βημάτων πολλαπλασιασμού, μειώνοντας αυτόν τον εκθέτη από n³ (για την τυπική μέθοδο) όσο μπορούν. Η χαμηλότερη δυνατή τιμή, n², είναι βασικά όσο χρειάζεται για να γράψετε την απάντηση. Οι επιστήμονες υπολογιστών αναφέρονται σε αυτόν τον εκθέτη ως ωμέγα, ω, με n^ω είναι τα λιγότερα δυνατά βήματα που απαιτούνται για τον επιτυχή πολλαπλασιασμό δύο n-με-n πίνακες ως n μεγαλώνει πολύ. «Το νόημα αυτής της δουλειάς», είπε ο Zhou, ο οποίος ήταν επίσης συν-συγγραφέας της εργασίας του Ιανουαρίου 2024, «είναι να δούμε πόσο κοντά στο 2 μπορείς να φτάσεις και αν μπορεί να επιτευχθεί θεωρητικά».

Μια εστίαση με λέιζερ

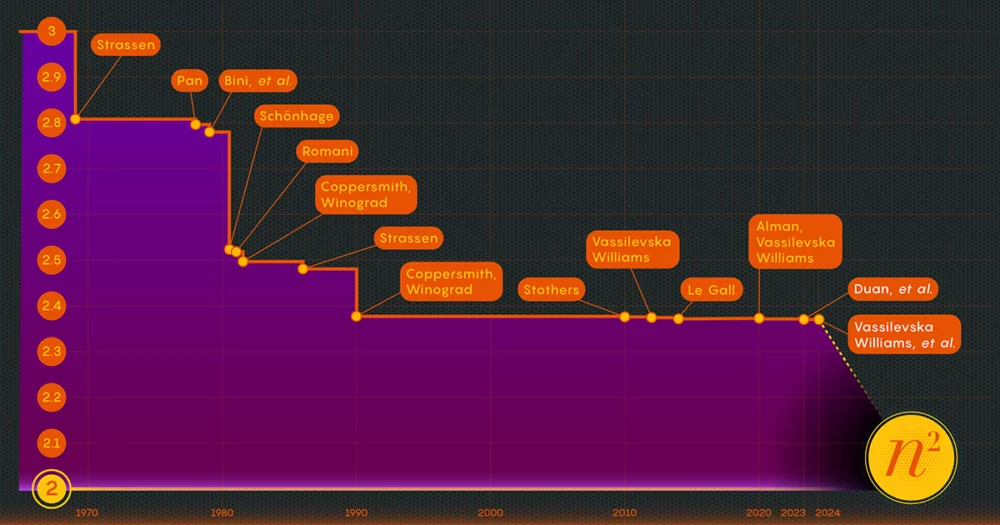
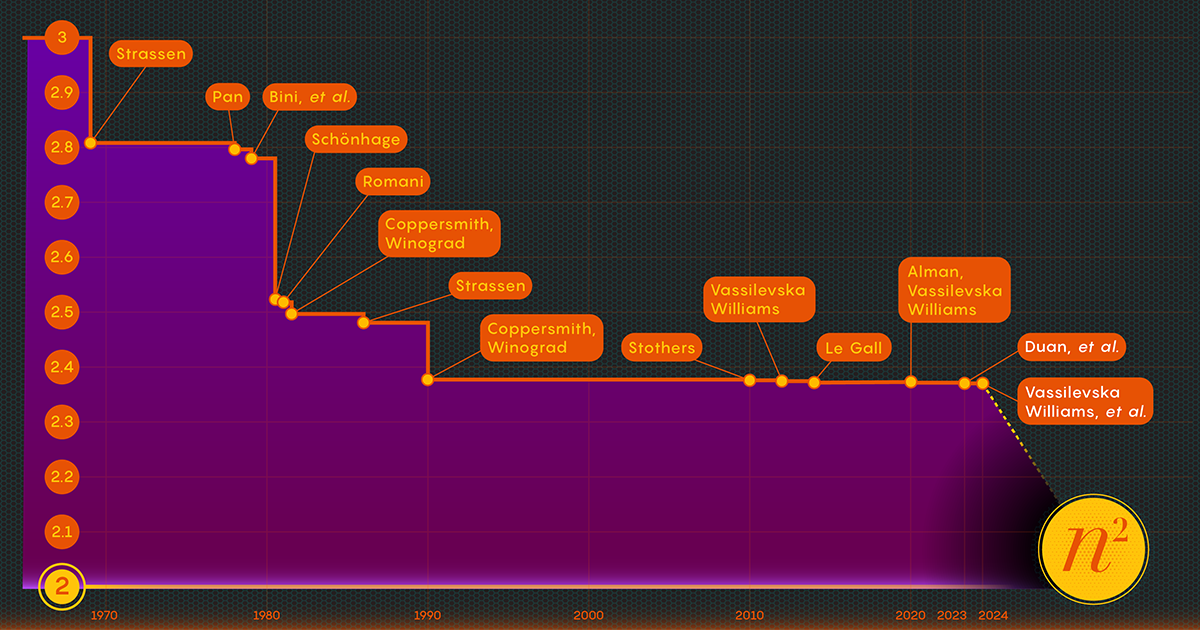
Το 1986, ο Strassen είχε άλλη μια μεγάλη ανακάλυψη όταν εισήγαγε αυτό που ονομάζεται μέθοδος λέιζερ για πολλαπλασιασμό πίνακα. Ο Strassen το χρησιμοποίησε για να καθορίσει μια ανώτερη τιμή για το ωμέγα 2.48. Ενώ η μέθοδος είναι μόνο ένα βήμα στους πολλαπλασιασμούς μεγάλων πινάκων, είναι ένα από τα πιο σημαντικά επειδή οι ερευνητές συνέχισαν να τη βελτιώνουν.

Ένα χρόνο αργότερα, ο Winograd και ο Don Coppersmith παρουσίασαν έναν νέο αλγόριθμο που συμπλήρωνε υπέροχα τη μέθοδο λέιζερ. Αυτός ο συνδυασμός εργαλείων εμφανίστηκε σχεδόν σε όλες τις επόμενες προσπάθειες για την επιτάχυνση του πολλαπλασιασμού πινάκων.

Ακολουθεί ένας απλοποιημένος τρόπος σκέψης για το πώς αυτά τα διαφορετικά στοιχεία ταιριάζουν μεταξύ τους. Ας ξεκινήσουμε με δύο μεγάλους πίνακες, τον Α και τον Β, που θέλετε να πολλαπλασιάσετε μαζί. Αρχικά, τα αποσυνθέτετε σε πολλές μικρότερες υπομήτρες ή μπλοκ, όπως ονομάζονται μερικές φορές. Στη συνέχεια, μπορείτε να χρησιμοποιήσετε τον αλγόριθμο του Coppersmith και του Winograd για να χρησιμεύσει ως ένα είδος εγχειριδίου οδηγιών για το χειρισμό και, τελικά, τη συναρμολόγηση των μπλοκ. «Μου λέει τι να πολλαπλασιάσω και τι να προσθέσω και ποιες εγγραφές πηγαίνουν πού» στον πίνακα γινομένων C, είπε η Vassilevska Williams. "Είναι απλώς μια συνταγή για να δημιουργήσετε το C από το Α και το Β."

Ωστόσο, υπάρχει ένα αλίευμα: μερικές φορές καταλήγετε με μπλοκ που έχουν κοινές καταχωρίσεις. Αν τα αφήσετε στο προϊόν θα ήταν παρόμοιο με το να μετράτε αυτές τις καταχωρήσεις δύο φορές, επομένως κάποια στιγμή θα πρέπει να απαλλαγείτε από αυτούς τους διπλότυπους όρους, που ονομάζονται επικαλύψεις. Οι ερευνητές το κάνουν αυτό «σκοτώνοντας» τα μπλοκ στα οποία βρίσκονται — θέτοντας τα στοιχεία τους ίσα με το μηδέν για να τα αφαιρέσουν από τον υπολογισμό.

Εκεί τελικά μπαίνει στο παιχνίδι η μέθοδος laser του Strassen. «Η μέθοδος λέιζερ συνήθως λειτουργεί πολύ καλά και γενικά βρίσκει έναν καλό τρόπο να σκοτώσει ένα υποσύνολο μπλοκ για να αφαιρέσει την επικάλυψη», είπε ο Le Gall. Αφού το λέιζερ εξαλείψει ή «κάψει» όλες τις επικαλύψεις, μπορείτε να κατασκευάσετε τη μήτρα τελικού προϊόντος, C.

Η συνένωση αυτών των διαφόρων τεχνικών οδηγεί σε έναν αλγόριθμο για τον πολλαπλασιασμό δύο πινάκων με έναν εσκεμμένα τσιμπημένο αριθμό πολλαπλασιασμών συνολικά — τουλάχιστον θεωρητικά. Η μέθοδος λέιζερ δεν προορίζεται να είναι πρακτική. είναι απλώς ένας τρόπος να σκεφτούμε τον ιδανικό τρόπο πολλαπλασιασμού πινάκων. «Δεν εκτελούμε ποτέ τη μέθοδο [σε υπολογιστή]», είπε ο Zhou. «Το αναλύουμε».

Και αυτή η ανάλυση είναι που οδήγησε στη μεγαλύτερη βελτίωση των ωμέγα σε περισσότερο από μια δεκαετία.

Βρέθηκε απώλεια

Η εφημερίδα του περασμένου καλοκαιριού, των Duan, Zhou και Wu, έδειξε ότι η διαδικασία του Strassen θα μπορούσε ακόμα να επιταχυνθεί σημαντικά. Όλα ήταν εξαιτίας μιας ιδέας που αποκαλούσαν κρυφή απώλεια, που ήταν θαμμένη βαθιά μέσα σε προηγούμενες αναλύσεις - «αποτέλεσμα ακούσιας θανάτωσης πάρα πολλών μπλοκ», είπε ο Zhou.

Η μέθοδος λέιζερ λειτουργεί με την επισήμανση των τεμαχίων με επικαλύψεις ως σκουπίδια, πλακοσκεπασμένα για απόρριψη. άλλα μπλοκ κρίνονται άξια και θα αποθηκευτούν. Η διαδικασία επιλογής, ωστόσο, είναι κάπως τυχαία. Ένα μπλοκ που χαρακτηρίζεται ως σκουπίδια μπορεί, στην πραγματικότητα, να αποδειχθεί χρήσιμο τελικά. Αυτό δεν ήταν μια απόλυτη έκπληξη, αλλά εξετάζοντας πολλές από αυτές τις τυχαίες επιλογές, η ομάδα του Duan διαπίστωσε ότι η μέθοδος λέιζερ υποτίμησε συστηματικά τα μπλοκ: Θα πρέπει να σωθούν περισσότερα μπλοκ και να πεταχτούν λιγότερα. Και, όπως συμβαίνει συνήθως, τα λιγότερα απόβλητα μεταφράζονται σε μεγαλύτερη αποτελεσματικότητα.

«Η δυνατότητα διατήρησης περισσότερων μπλοκ χωρίς επικάλυψη οδηγεί σε … έναν ταχύτερο αλγόριθμο πολλαπλασιασμού πινάκων», είπε ο Le Gall.

Αφού απέδειξε την ύπαρξη αυτής της απώλειας, η ομάδα του Duan τροποποίησε τον τρόπο με τον οποίο η μέθοδος λέιζερ σήμανε τα μπλοκ, μειώνοντας σημαντικά τα απόβλητα. Ως αποτέλεσμα, έθεσαν ένα νέο ανώτερο όριο για τα ωμέγα περίπου στο 2.371866 — μια βελτίωση σε σχέση με το προηγούμενο ανώτερο όριο των 2.3728596, γυρίστηκε το 2020 από τους Josh Alman και Vassilevska Williams. Αυτό μπορεί να φαίνεται σαν μια μέτρια αλλαγή, μειώνοντας το όριο κατά περίπου 0.001. Αλλά είναι η μοναδική μεγαλύτερη βελτίωση που έχουν δει οι επιστήμονες από το 2010. Το αποτέλεσμα του 2020 των Vassilevska Williams και Alman, συγκριτικά, βελτιώθηκε μόνο κατά 0.00001 σε σχέση με τον προκάτοχό του.

Αλλά αυτό που είναι πιο συναρπαστικό για τους ερευνητές δεν είναι μόνο ο νέος δίσκος, ο οποίος δεν κράτησε πολύ. Είναι επίσης το γεγονός ότι η εφημερίδα αποκάλυψε μια νέα οδό βελτίωσης που μέχρι τότε περνούσε εντελώς απαρατήρητη. Για σχεδόν τέσσερις δεκαετίες, όλοι βασίζονται στην ίδια μέθοδο λέιζερ, είπε ο Le Gall. «Τότε διαπίστωσαν ότι, λοιπόν, μπορούμε να τα πάμε καλύτερα».

Το έγγραφο του Ιανουαρίου 2024 βελτίωσε αυτή τη νέα προσέγγιση, επιτρέποντας στους Vassilevska Williams, Zhou και στους συν-συγγραφείς τους να μειώσουν περαιτέρω την κρυφή απώλεια. Αυτό οδήγησε σε μια πρόσθετη βελτίωση του ανώτερου ορίου των ωμέγα, μειώνοντάς το σε 2.371552. Οι συγγραφείς γενίκευσαν επίσης την ίδια τεχνική για να βελτιώσουν τη διαδικασία πολλαπλασιασμού για ορθογώνια (n-με-m) πίνακες — μια διαδικασία που έχει εφαρμογές στη θεωρία γραφημάτων, τη μηχανική μάθηση και άλλους τομείς.

Κάποια περαιτέρω πρόοδος προς αυτές τις γραμμές είναι σχεδόν βέβαιη, αλλά υπάρχουν όρια. Το 2015, ο Le Gall και δύο συνεργάτες του αποδείχθηκε ότι η τρέχουσα προσέγγιση - η μέθοδος λέιζερ σε συνδυασμό με τη συνταγή Coppersmith-Winograd - δεν μπορεί να αποφέρει ωμέγα κάτω από 2.3078. Για να κάνετε περαιτέρω βελτιώσεις, ο Le Gall είπε, «πρέπει να βελτιώσετε την αρχική [προσέγγιση] των Coppersmith και Winograd που δεν έχει αλλάξει πραγματικά από το 1987. " Αλλά μέχρι στιγμής, κανείς δεν έχει βρει καλύτερο τρόπο. Μπορεί να μην υπάρχει καν ένα.

«Η βελτίωση των ωμέγα είναι στην πραγματικότητα μέρος της κατανόησης αυτού του προβλήματος», είπε ο Zhou. «Αν μπορούμε να κατανοήσουμε καλά το πρόβλημα, τότε μπορούμε να σχεδιάσουμε καλύτερους αλγόριθμους για αυτό. [Και] οι άνθρωποι είναι ακόμα σε πολύ πρώιμα στάδια κατανόησης αυτού του πανάρχαιου προβλήματος».