سورپرایز اثبات علوم کامپیوتر ریاضیدانان را شگفت زده می کند

روز یکشنبه، 5 فوریه، اولوف سیساسک و توماس بلوم ایمیلی دریافت کردند که حاوی یک پیشرفت خیره کننده در مورد بزرگترین مشکل حل نشده در حوزه کاری خود بود. زندر کلی، دانشجوی کارشناسی ارشد در دانشگاه ایلینوی، اوربانا شامپین، سیساسک و بلوم را فرستاده بود. مقاله ای که نوشته بود با راگو مکا از دانشگاه کالیفرنیا، لس آنجلس. هم کلی و هم مکا دانشمندان کامپیوتر بودند، دنیایی فکری جدا از ترکیب‌های ترکیبی که سیساسک و بلوم مطالعه می‌کنند.

"ذهن من فقط منفجر شده بود. مثلاً صبر کنید، آیا آنها واقعاً این کار را کرده‌اند؟» سیساسک، مدرس دانشگاه استکهلم گفت. کلی و مکا، افراد خارجی در زمینه ترکیبیات، گفتند که یک محدودیت جدید - و به طور چشمگیری کمتر - در اندازه مجموعه ای از اعداد صحیح یافته اند که در آن هیچ سه عدد از آنها به طور مساوی فاصله ندارند (ترکیبی مانند 3، 8 و 13 را رد می کند. یا 101، 201 و 301).

ادعای کلی و مکا رکورد قبلی را شکست، در سال 2020 به دست آمد توسط سیساسک و بلوم، که یک محقق در دانشگاه آکسفورد است. بن گرین، یکی از همکاران بلوم در آکسفورد، می‌گوید: «کار بلوم و سیساسک - کار بسیار قوی که بود - واقعاً این تصور را ایجاد کرد که بهبود آن بسیار دشوار است. "به نظر می رسید در جایی که بود بسیار گیر کرده بود."

اگرچه بلوم و سیساسک در زمان دریافت ایمیل، مسائل مهم دیگری داشتند که باید به آنها رسیدگی کنند - بلوم به تازگی یک توله سگ را به فرزندی قبول کرده بود، در حالی که سیساسک در میانه حرکت بود - آنها به سرعت دست به کار شدند تا مقاله جدید را تأیید کنند.

در عرض چند روز، بلوم و سیساسک متقاعد شدند که اثبات جدید درست است. سیساسک آن را "بزرگترین نتیجه در 20 سال گذشته در منطقه" خواند. آن‌ها که مشتاق بودند دیگران از ایده‌های کلی و مکا قدردانی کنند، پیش‌نویس کردند گزارش توضیح برهان با عباراتی که برای ریاضیدانان آشناتر است.

مکا گفت که پاسخ جامعه «مثبت‌تر از آنچه فکر می‌کردم بوده است. دیدن همه بازخوردها شگفت انگیز است."

پیشرفت طولانی

دنباله‌ای از اعداد با فاصله مساوی که کلی و مکا به دنبال اجتناب از آنها بودند، پیشرفت‌های حسابی نامیده می‌شوند. آنها می توانند برای همیشه ادامه یابند یا فقط شامل چند عبارت باشند. کلی و مکا بر روی پیشرفت هایی که فقط از سه عدد تشکیل شده بود، به دنبال یک خط تحقیقاتی که اغلب به یک مقاله 1936 توسط Paul Erdős و Paul Turán.

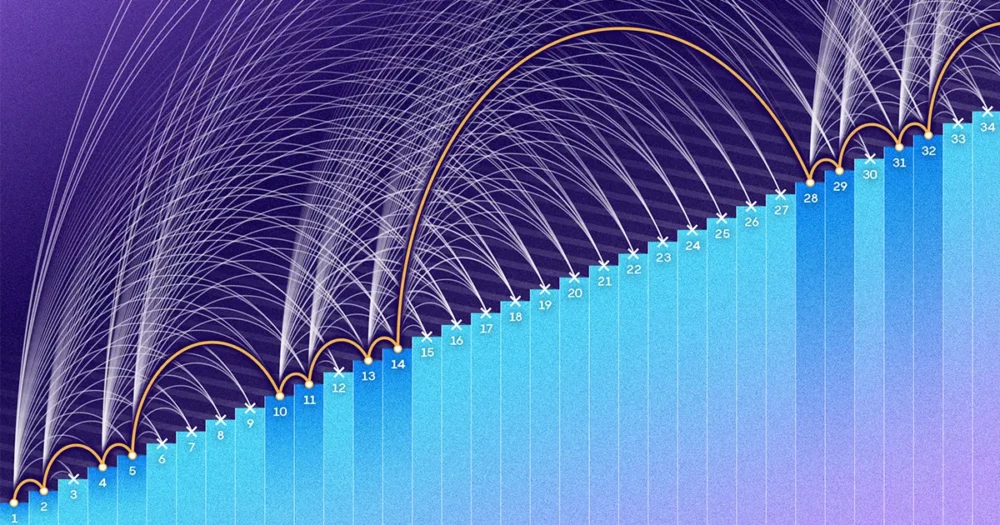
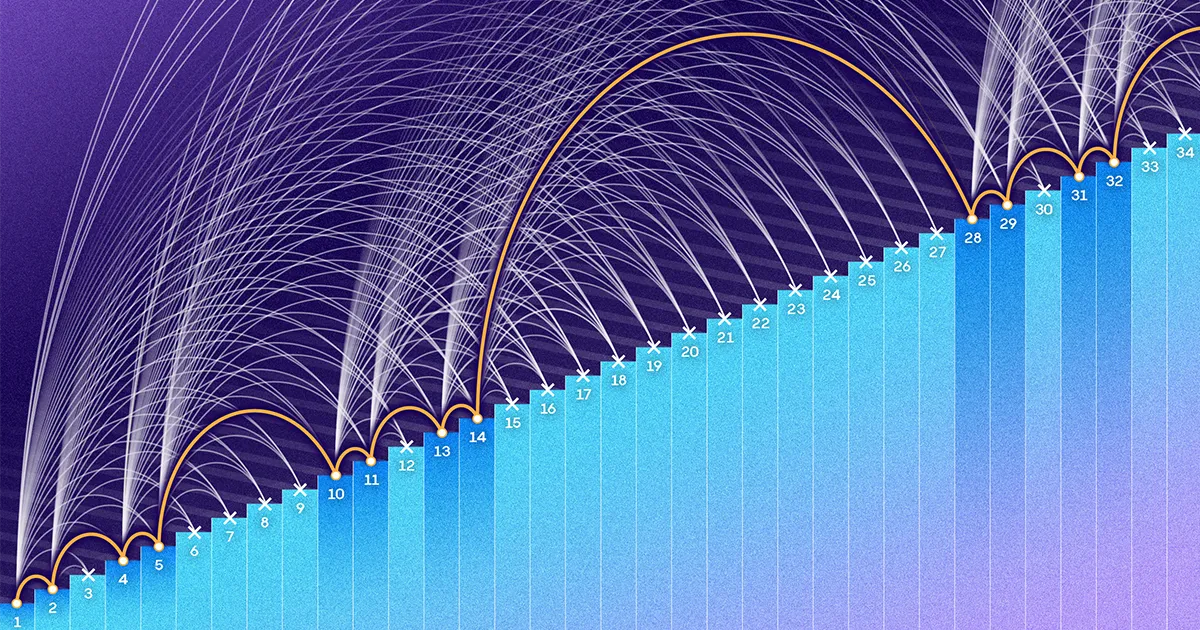
Erdős و Turán می خواستند بدانند چند عدد از سقف کوچکتر است N را می توان بدون ایجاد هیچ پیشروی حسابی سه جمله ای در یک مجموعه قرار داد. N ممکن است 1,000، 1 میلیون یا مقداری غیرقابل تصور بزرگ باشد. آنها حدس زدند که به عنوان N بزرگ‌تر می‌شد، مجموعه‌ای بدون پیشرفت‌های سه‌ترمی باید به‌طور باورنکردنی پراکنده می‌شد. ایجاد چنین مجموعه ای مانند جمع آوری کفش است و در عین حال اصرار دارد که دو جفت همرنگ نباشند. شاید بتوانید برای همیشه ادامه دهید، اما با بزرگ‌تر شدن مجموعه‌تان، متوجه می‌شوید که با سرعت کمتر و آهسته‌تری به آن اضافه می‌کنید.

مکا توضیح داد: «ساختاری وجود دارد که بدون توجه به اینکه چگونه مجموعه را انتخاب کرده اید، در مجموعه ظاهر می شود. "شما واقعاً به چه اندازه بزرگ نیاز دارید تا تضمین کنید که این ساختار در آن وجود دارد؟"

در سال 1946، فلیکس بهرند راهی برای ساخت مجموعه ها پیدا کرد از اعداد بین 1 و N بدون ایجاد هیچ پیشرفت سه دوره ای. روش او منجر به ست هایی شد که بزرگتر شدند N انجام داد، اما دردناک به آرامی. چه زمانی N 100,000 است، مجموعه Behrend فقط شامل 171 عنصر است. چه زمانی N 1 میلیون است، مجموعه او 586 عدد دارد - کمتر از 0.06٪ از اعداد بین 1 تا 1 میلیون.

مجموعه‌های Behrend به ریاضیدانان فرصتی برای کار می‌دهد: بزرگترین مجموعه بدون پیشرفت سه ترم باید حداقل به بزرگی بهند باشد. در سال 1953، کلاوس راث سقفی را فراهم کرد، یافتن آستانه ای که یک مجموعه ناگزیر باید دارای یک پیشرفت سه دوره ای باشد.

راث حدس اردوس و توران را با نشان دادن آن ثابت کرده بود N بزرگ‌تر می‌شود، مجموعه‌ای بدون پیشرفت‌های سه ترم، کسری کوچک‌تر از اعداد بین 1 و N را شامل می‌شود. اما سقف راث با کف بهند فاصله زیادی داشت. Behrend نشان داده بود که 0.06٪ از عناصر بین 1 تا 1 میلیون می توانند در یک مجموعه بدون پیشرفت قرار بگیرند. اگرچه محاسبه دقیق فرمول راث سخت است، اما به آن پایین هم نزدیک نیست - یک تخمین تقریبی این درصد را در حدود 40 درصد محدود کرده است.

اما برجسته تر از آن شکاف خاص، رفتار کلی دو فرمول بود. کسر عناصر را بین 1 و رسم کنید N که هر فرمول نشان دهنده آن است، و خواهید دید که عدد Behrend به سرعت به صفر کاهش می یابد N رشد می کند. از سوی دیگر، کسر راث به سمت صفر می لغزد، اما به آرامی و به آرامی. این دو منحنی شکل‌های بسیار متفاوتی دارند و نسبت واقعی عناصری که در یک مجموعه بدون پیشروی‌های حسابی قرار دارند، می‌تواند، تا آنجا که ریاضیدانان می‌دانستند، در هر نقطه‌ای بین آنها قرار داشته باشد.

گرین گفت: با شروع دهه 1980، "توالی طولانی از پیشرفت های نسبتاً تدریجی، در آینده، توسط تعداد زیادی از ریاضیدانان واقعا معروف وجود داشت." هر چند وقت یک‌بار، شخصی حد بالایی راث را یک یا دو تار مو پایین می‌آورد و در نهایت به میزان قابل توجهی پایین‌تر می‌آمد. در مقابل، کران پایینی Behrend برای چندین دهه تکان نخورد. بلوم گفت که ریاضیدانان شروع به فکر کردن کردند که شاید بهند از پاسخ واقعی دور نبوده باشد.

تا زمانی که مقاله کلی و مکا در اوایل سال 2023 رسید، حداکثر اندازه یک مجموعه بدون پیشرفت از پایین توسط فرمول Behrend و از بالا توسط Bloom و Sisask نوشته می شد. مقاله بلوم و سیساسک از ژوئیه 2020 با نشان دادن اینکه یک مجموعه بدون پیشرفت باید به میزان قابل توجهی کمتر از آستانه لگاریتمی بحرانی باشد N/(ورود N) عناصر. اما نتیجه آنها همچنان بالاتر از بهند بود. کران فوقانی جدید کلی و مکا به شدت به زمینی که بهرند تعیین کرده نزدیک تر است.

ترنس تائو، ریاضیدان برجسته دانشگاه UCLA، گفت: «مکا و کلی به نوعی از این پیشرفت تدریجی جهش کردند.

فرمول آنها تقریباً مشابه فرمول Behrend است و فقط چند پارامتر بهینه شده است. مانند N با نزدیک شدن به بی نهایت، طرحی از فرمول کلی و مکا در نهایت در منحنی شبیه به منحنی بهرن قرار می گیرد. بلوم می‌گوید: «هر محدودیتی از این شکل قبلاً رویایی غیرممکن به نظر می‌رسید.

گرین گفت: «من واقعاً کاملاً متحیر بودم که آنها چنین پیشرفتی را ایجاد کرده بودند.

یک تکه متفاوت

 اگرچه کلی و مکا پیش از این هرگز به طور کامل به تحقیقات ریاضیات محض نپرداخته بودند، پیشروی‌های محاسباتی هنگام شروع برای آنها آشنا بود. کلی گفت، به طور کلی، دانشمندان کامپیوتر "با تشنگی به دنبال تکنیک هایی هستند که برای حل مشکلات ما کار کنند." ابزارهایی که در طول تاریخ برای مطالعه اندازه یک مجموعه بدون پیشرفت مورد استفاده قرار می‌گرفتند، به طور گسترده در زیر شاخه علوم کامپیوتر نظریه پیچیدگی استفاده می‌شدند. مشکل محدود کردن اندازه چنین مجموعه ای برای نظریه پردازان پیچیدگی به عنوان مثالی اساسی از به کارگیری تکنیک هایی که ساختار درونی مجموعه ها را بررسی می کند، شناخته شده است.

در اواخر سال 2021، کلی و مکا در حال تجزیه و تحلیل شانس این بودند که یک تیم از بازیکنان در یک بازی مشترک خاص، یک نوع استاندارد از مشکلات علوم کامپیوتر، بتوانند برنده شوند. به ذهن آنها رسید که تکنیک های تحقیق در مورد اندازه مجموعه های بدون پیشرفت ممکن است مفید باشد. اما مطالعه مستقیم آن تکنیک ها را آسان تر از به کار بردن آنها در بازی مشارکتی یافتند. کلی گفت: «بهترین ایده من برای چگونگی پیشرفت در این مشکل [این بود] که در واقع خود ابزار را بهبود بخشم، نه اینکه از آن به روشی هوشمندانه استفاده کنم.

مکا به یاد می آورد: «در مقطعی، ما تصمیم گرفتیم مستقیماً روی این سؤال کار کنیم. شش ماه بعد، این دو محقق استراتژی خود را کشف کرده بودند و فقط باید روش استفاده از روش خود را برای مشکل مورد نظر مشخص کنند.

برای اینکه ببینید چگونه به حد بالایی جدید خود رسیده اند، هر مجموعه ای از اعداد را بین 1 و در نظر بگیرید N. صداش کن A. تراکم A درصد اعداد بین 1 و N که شامل می شود. از آنجایی که تعداد زیادی پیشروی محاسباتی بین 1 و وجود دارد N، اگر عناصر را انتخاب نکنید A با دقت، هر A با چگالی بالا احتمالاً دارای تعداد زیادی پیشرفت های حسابی است.

کلی و مکا در اثبات خود چنین تصور کردند A پیشرفت های حسابی کمی داشتند یا اصلاً هیچ پیشرفتی نداشتند، و سعی کردند پیامدهای آن را ردیابی کنند. اگر A به اندازه کافی متراکم بود، آنها نشان دادند که فقدان پیشرفت ها نیاز به سطحی از ساختار درونی دارد A که به ناچار منجر به تناقض می شود، به این معنی که A پس از همه، باید حداقل یک پیشرفت داشته باشد.

برای درک آن ساختار، مجموعه را در نظر گرفتند A + A، که از تمام اعداد ساخته شده با جمع دو عنصر تشکیل شده است A. آنها متوجه شدند که اگر A شامل پیشرفت های محاسباتی نسبتاً کمی است، این به معنای افزونگی در بین عناصر است A + A: جفت های مختلف اعداد از A اغلب به یک عدد اضافه می شود.

چگالی را می توان نه تنها در مقایسه با تمام اعداد صحیح بین 1 و تعریف کرد N اما در مقایسه با برخی از زیرمجموعه ها - فقط اعداد صحیح زوج در آن بازه، یا فقط مضرب های 3 را بگویید. Kelley و Meka از افزونگی ها در آن استفاده کردند. A + A برای پیدا کردن زیر مجموعه ای از اعداد صحیح که عناصر A به خصوص رایج بودند.

برای مثال، اگر A به طور نامتناسبی دارای مضرب های 3 باشد، کلی و مکا روی بخشی که مضرب 3 را شامل می شود تمرکز می کنند. آنها این استراتژی را بارها و بارها تکرار کردند. هر بار زیر مجموعه‌های کوچک‌تر و کوچک‌تری از اعداد صحیح پیدا می‌کردند Aتراکم به رشد و رشد ادامه خواهد داد. مثلا، A ممکن است شامل 10٪ از اعداد صحیح بین 1 و N15% از مضرب های 3 در آن بازه و 25% از مضرب های زوج 3.

وقتی اتفاق جالبی می افتد A بزرگ است اگر این روش تکرار شود، چگالی از A بیش از برخی از زیر مجموعه ها بیش از 100٪ است. که البته غیرممکن است. A مثلاً می‌تواند شامل همه مضرب‌های 24 باشد، اما نمی‌تواند بیش از همه آنها را شامل شود. این پارادوکس تنها در صورتی به وجود می آید که A برای شروع به اندازه کافی بزرگ است، اما وقتی این کار را انجام داد، به این معنی است که این فرضیه A هیچ پیشروی حسابی ندارد حتما اشتباه بوده است.

این یک «استدلال برد-برد» است، وقتی A مکا گفت بزرگ است. هر دو A شامل تعداد زیادی پیشروی حسابی است، یا افزونگی زیادی در آن وجود دارد A + A - در این صورت آنها می توانند از روش یافتن زیرمجموعه (به نام "استراتژی افزایش تراکم") استفاده کنند تا نشان دهند که یک پیشرفت باید در A. اگرچه استراتژی افزایش تراکم طرحی است که در این زمینه به خوبی فرسوده شده است، اما Kelley و Meka توانستند آن را برای کوچکترها کار کنند. Aنسبت به قبل با آن، آنها سقف جدیدی را برای اندازه یک مجموعه بدون پیشرفت کشف کردند.

کلی و مکا ترکیبی منحصر به فرد از ایده ها را از طرح افزایش چگالی ساختند. آنها به جای ارائه یک چارچوب کاملاً جدید، روشی را که زیرمجموعه متراکم خود را پیدا کردند، دوباره بررسی کردند. برای این کار، آنها از تکنیکی استفاده کردند که آن را «الک کردن» نامیدند، که شامل جابجایی مجموعه آنها با مقدار ثابت، تقاطع آن با خودش و تکرار این فرآیند چندین و چند بار است. آنچه باقی می ماند، پس از چندین دور تقاطع، مجموعه ای بسیار ساختار یافته با ویژگی های قابل پیش بینی است. اگرچه غربال کردن در مقالات دیگر مورد استفاده قرار گرفته است، اما هرگز در مورد مشکل پیشرفت سه ترم آزمایش نشده است.

نگاه به عقب

Kelley و Meka با تزریق ابزارهای نادیده گرفته شده مانند الک کردن به روش های سنتی، محدودیت اندازه مجموعه بدون پیشرفت را به میزان تکان دهنده ای کاهش دادند. بلوم گفت: «کلی و مکا به ما نشان داده‌اند که این تکنیک‌ها، که در فضای باز وجود داشتند، بسیار قوی‌تر از آن چیزی بودند که ما گمان می‌کردیم.» او افزود، با توجه به اثربخشی جدید این ابزارها، "ما باید به عقب برگردیم و همه چیز را دوباره بررسی کنیم."

استراتژی افزایش چگالی اولین بار در مقاله راث 70 سال پیش ظاهر شد و از آن زمان در بیشتر مقالات در مورد پیشرفت های حسابی استفاده شده است. گرین متعجب بود که از این چارچوب می‌توان برای اثبات محدودیتی به اندازه کلی و مکا استفاده کرد. او گفت: "من فکر می کردم چیزی کاملاً متفاوت مورد نیاز است."

کلی هیجان زده است که به تلاش خود در ریاضیات ادامه دهد. او گفت: "من در مورد بسیاری از مشکلات مختلف که حداقل از نظر روحی به این موضوع مربوط می شود، امید و آرزو ندارم."

اینکه کلی و مکا موفق شدند قدرت ایده‌هایی را که زمانی نادیده گرفته می‌شد، تشخیص دهند، ماهیت غالباً نامناسب پیشرفت ریاضی را نشان می‌دهد - کیفیتی که برای تائو بیشتر یک موهبت است تا یک نفرین. او گفت: «همیشه اینطور نیست که ریاضی سخت‌تر و سخت‌تر و سخت‌تر شود. "خدا را شکر."