Le clustering K-means est un algorithme d'apprentissage non supervisé qui regroupe les données en fonction de la distance euclidienne de chaque point à un point central appelé centroïde. Les centroïdes sont définis au moyen de tous les points qui se trouvent dans le même cluster. L'algorithme choisit d'abord des points aléatoires comme centroïdes, puis itère en les ajustant jusqu'à la convergence complète.
Une chose importante à retenir lors de l'utilisation de K-means, c'est que le nombre de clusters est un hyperparamètre, il sera défini avant d'exécuter le modèle.
K-means peut être implémenté à l'aide de Scikit-Learn avec seulement 3 lignes de code. Scikit-learn a également déjà une méthode d'optimisation centroïde disponible, kméens++, qui aide le modèle à converger plus rapidement.
Pour appliquer l'algorithme de clustering K-means, chargeons le Pingouins palmiers jeu de données, choisissez les colonnes qui seront regroupées et utilisez Seaborn pour tracer un nuage de points avec des clusters codés par couleur.
Notes: Vous pouvez télécharger le jeu de données à partir de ce lien.
Importons les bibliothèques et chargeons le jeu de données Penguins, en le découpant dans les colonnes choisies et en supprimant les lignes avec des données manquantes (il n'y en avait que 2):
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
df = pd.read_csv('penguins.csv')
print(df.shape)
df = df[['bill_length_mm', 'flipper_length_mm']]
df = df.dropna(axis=0)
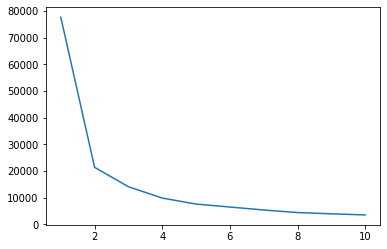
Nous pouvons utiliser la méthode Elbow pour avoir une indication des clusters pour nos données. Elle consiste en l'interprétation d'un tracé linéaire en forme de coude. Le nombre de grappes correspond aux coudes. L'axe x du graphique est le nombre de clusters et l'axe y est la somme des carrés dans les clusters (WCSS) pour chaque nombre de clusters :
wcss = []
for i in range(1, 11):
clustering = KMeans(n_clusters=i, init='k-means++', random_state=42)
clustering.fit(df)
wcss.append(clustering.inertia_)
ks = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
sns.lineplot(x = ks, y = wcss);
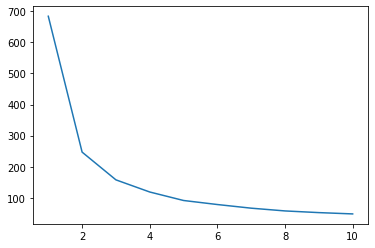
La méthode du coude indique que nos données ont 2 clusters. Traçons les données avant et après le clustering :
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(15,5))
sns.scatterplot(ax=axes[0], data=df, x='bill_length_mm', y='flipper_length_mm').set_title('Without clustering')
sns.scatterplot(ax=axes[1], data=df, x='bill_length_mm', y='flipper_length_mm', hue=clustering.labels_).set_title('Using the elbow method');
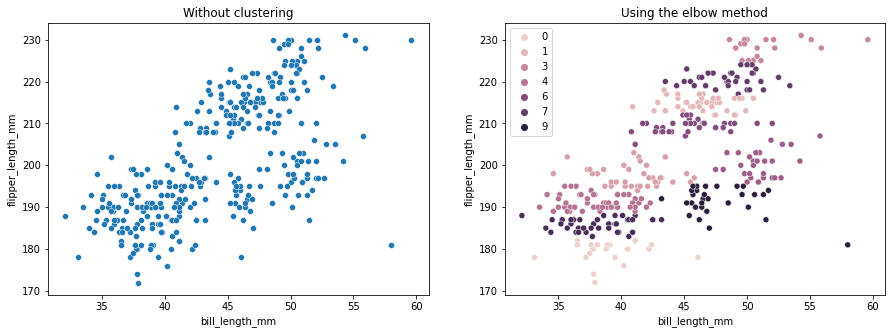
Cet exemple montre comment la méthode Elbow n'est qu'une référence lorsqu'elle est utilisée pour choisir le nombre de clusters. Nous savons déjà que nous avons 3 types de pingouins dans l'ensemble de données, mais si nous devions déterminer leur nombre en utilisant la méthode Elbow, 2 clusters seraient notre résultat.
Étant donné que K-means est sensible à la variance des données, examinons les statistiques descriptives des colonnes que nous regroupons :
df.describe().T
Cela se traduit par:
count mean std min 25% 50% 75% max
bill_length_mm 342.0 43.921930 5.459584 32.1 39.225 44.45 48.5 59.6
flipper_length_mm 342.0 200.915205 14.061714 172.0 190.000 197.00 213.0 231.0
Notez que la moyenne est loin de l'écart type (std), cela indique une variance élevée. Essayons de le réduire en mettant à l'échelle les données avec Standard Scaler :
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
scaled = ss.fit_transform(df)
Maintenant, répétons le processus de la méthode Elbow pour les données mises à l'échelle :
wcss_sc = []
for i in range(1, 11):
clustering_sc = KMeans(n_clusters=i, init='k-means++', random_state=42)
clustering_sc.fit(scaled)
wcss_sc.append(clustering_sc.inertia_)
ks = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
sns.lineplot(x = ks, y = wcss_sc);
Consultez notre guide pratique et pratique pour apprendre Git, avec les meilleures pratiques, les normes acceptées par l'industrie et la feuille de triche incluse. Arrêtez de googler les commandes Git et en fait apprendre il!
Cette fois, le nombre de clusters suggéré est de 3. Nous pouvons à nouveau tracer les données avec les étiquettes de cluster avec les deux anciens tracés à des fins de comparaison :
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(15,5))
sns.scatterplot(ax=axes[0], data=df, x='bill_length_mm', y='flipper_length_mm').set_title('Without cliustering')
sns.scatterplot(ax=axes[1], data=df, x='bill_length_mm', y='flipper_length_mm', hue=clustering.labels_).set_title('With the Elbow method')
sns.scatterplot(ax=axes[2], data=df, x='bill_length_mm', y='flipper_length_mm', hue=clustering_sc.labels_).set_title('With the Elbow method and scaled data');
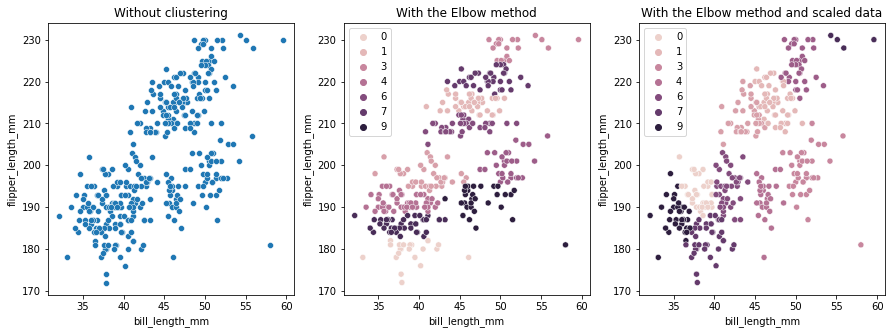
Lorsque vous utilisez le clustering K-means, vous devez prédéterminer le nombre de clusters. Comme nous l'avons vu lors de l'utilisation d'une méthode pour choisir notre k nombre de clusters, le résultat n'est qu'une suggestion et peut être influencé par la quantité de variance dans les données. Il est important de mener une analyse approfondie et de générer plus d'un modèle avec différents _k_s lors du clustering.
S'il n'y a aucune indication préalable du nombre de clusters dans les données, visualisez-les, testez-les et interprétez-les pour voir si les résultats du clustering ont du sens. Si ce n'est pas le cas, regroupez à nouveau. En outre, examinez plus d'une métrique et instanciez différents modèles de clustering - pour K-means, regardez le score de silhouette et peut-être le clustering hiérarchique pour voir si les résultats restent les mêmes.