A kvantumsebesség-torzítás függvény hatékony számítása

Újra kiadta Platón

Követő: 0

Efficient Computation of the Quantum Rate-Distortion Function PlatoBlockchain Data Intelligence. Vertical Search. Ai.

Kerry Ő¹, James Saunderson¹és Hamza Fawzi²

¹Elektromos és Számítógépes Rendszermérnöki Tanszék, Monash Egyetem, Clayton VIC 3800, Ausztrália
²Alkalmazott Matematika és Elméleti Fizika Tanszék, Cambridge-i Egyetem, Cambridge CB3 0WA, Egyesült Királyság

Érdekesnek találja ezt a cikket, vagy szeretne megvitatni? Scite vagy hagyjon megjegyzést a SciRate-en.

Absztrakt

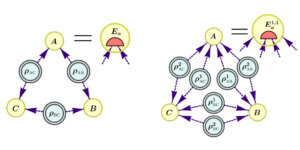
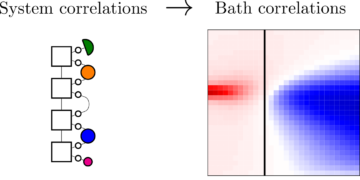
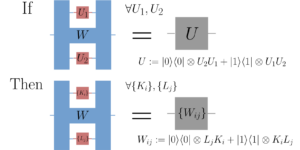
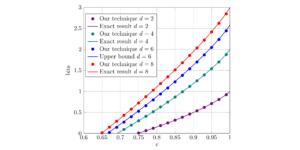
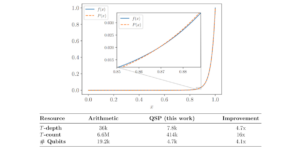
A kvantumsebesség-torzítás függvény alapvető szerepet játszik a kvantuminformáció-elméletben, azonban jelenleg nincs olyan gyakorlati algoritmus, amely ezt a függvényt hatékonyan, nagy pontossággal mérsékelt csatornadimenziók esetén tudná kiszámítani. Ebben a cikkben bemutatjuk, hogy a szimmetriacsökkentés hogyan képes jelentősen leegyszerűsíteni az összefonódással segített kvantumsebesség-torzítási problémák gyakori előfordulásait. Ez lehetővé teszi számunkra, hogy jobban megértsük a kvantumcsatornák tulajdonságait, amelyek az optimális sebesség-torzítás kompromisszumot biztosítják, ugyanakkor lehetővé teszi a kvantumsebesség-torzítási függvény hatékonyabb kiszámítását, függetlenül az alkalmazott numerikus algoritmustól. Ezenkívül a tükör süllyedési algoritmus egy pontatlan változatát javasoljuk a kvantumsebesség-torzítási függvény kiszámításához bizonyítható szublineáris konvergencia sebességekkel. Megmutatjuk, hogy ez a tükörsüllyedés-algoritmus hogyan kapcsolódik a Blahut-Arimotohoz és a korábban hasonló információelméleti problémák megoldására használt elvárás-maximalizálási módszerekhez. Ezekkel a technikákkal bemutatjuk az első numerikus kísérleteket egy többkbites kvantumsebesség-torzítási függvény kiszámítására, és megmutatjuk, hogy az általunk javasolt algoritmus gyorsabban és nagyobb pontossággal oldja meg a meglévő módszerekhez képest.

Népszerű összefoglaló

A kvantumsebesség-torzítás függvény azt a maximális mennyiséget írja le, amennyit egy kvantum információforrás egy kvantumcsatornával tömöríthet anélkül, hogy túllépné a megengedett maximális torzítást. Általában ezt a függvényt numerikusan kell kiszámítani egy konvex optimalizálási feladat megoldásával. Ez azonban két okból is kihívást jelenthet. Először is, az optimalizálási probléma problémadimenziója gyorsan megnő, ahogy a kvantumcsatorna mérete növekszik. A kvantum információforrás torzításának mérésére szolgáló általános módszereknél bemutatjuk, hogyan lehet az optimalizálási probléma szimmetriáit kihasználni az optimalizálási probléma dimenziójának jelentős csökkentésére, lehetővé téve a probléma sokkal gyorsabb megoldását. Másodszor, a szabványos gradiens süllyedő algoritmusok nem működnek jól a kvantumsebesség-torzítás függvény kiszámításakor, az optimalizálási probléma során felmerülő kvantumentrópia-szerű függvények miatt. Ehelyett bemutatjuk, hogyan használható a gradiens süllyedés entrópikus variációja, amelyet entrópikus tükör süllyedésként ismerünk, hogy hatékony algoritmust állítsunk elő a kvantumsebesség-torzítási függvény kiszámításához.

► BibTeX adatok

@article{He2024 hatékony, doi = {10.22331/q-2024-04-09-1314}, url = {https://doi.org/10.22331/q-2024-04-09-1314}, title = {A {Q}uantum {R}ate-{D}torzítás {F}funkció} hatékony {C}számítása, szerző = {Ő, Kerry és Saunderson, James és Fawzi, Hamza}, folyóirat = {{Kvantum}}, issn = {2521-327X}, kiadó = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, hangerő = {8}, oldalak = {1314}, hónap = ápr, év = {2024} }

► Referenciák

[1] Claude Elwood Shannon „A kommunikáció matematikai elmélete” The Bell System Technical Journal 27, 379-423 (1948).
https:///doi.org/10.1002/j.1538-7305.1948.tb01338.x

[2] Nilanjana Datta, Min-Hsiu Hsieh és Mark M. Wilde, „Kvantumsebességű torzítás, fordított Shannon-tételek és forrás-csatorna szétválasztás”, IEEE Transactions on Information Theory 59, 615–630 (2013).
https:///doi.org/10.1109/tit.2012.2215575

[3] Mark M Wilde, Nilanjana Datta, Min-Hsiu Hsieh és Andreas Winter, „Quantum rate-distortion coding with auxiliary resources” IEEE Transactions on Information Theory 59, 6755–6773 (2013).
https:///doi.org/10.1109/tit.2013.2271772

[4] Richard Blahut „Csatorna kapacitásának és sebesség-torzítási függvényeinek számítása” IEEE Transactions on Information Theory 18, 460–473 (1972).
https:///doi.org/10.1109/tit.1972.1054855

[5] Suguru Arimoto „Algoritmus tetszőleges diszkrét memória nélküli csatornák kapacitásának kiszámításához” IEEE Transactions on Information Theory 18, 14–20 (1972).
https:///doi.org/10.1109/tit.1972.1054753

[6] Kerry He, James Saunderson és Hamza Fawzi: „Bregman proximális perspektíva a klasszikus és kvantum Blahut-Arimoto algoritmusokról” (2023).
arXiv: 2306.04492

[7] Arkadij Semenovič Nemirovskijand David Borisovich Yudin „Probléma komplexitás és módszer hatékonysága az optimalizálásban” Wiley (1983).

[8] Amir Beckand Marc Teboulle „Tükör süllyedés és nemlineáris vetített szubgradiens módszerek konvex optimalizáláshoz” Operations Research Letters 31, 167–175 (2003).
https://doi.org/10.1016/s0167-6377(02)00231-6

[9] Paul Tseng „A konvex-konkáv optimalizálás gyorsított proximális gradiens módszereiről” jelentés (2008).
https:///pages.cs.wisc.edu/~brecht/cs726docs/Tseng.APG.pdf

[10] Amir Beck „Elsőrendű módszerek az optimalizálásban” SIAM (2017).
https:///doi.org/10.1137/1.9781611974997

[11] Heinz H Bauschke, Jérôme Bolte és Marc Teboulle, „Egy leszállási lemma a Lipschitz-gradiens folytonosságon túl: Elsőrendű módszerek újralátogatása és alkalmazások” Mathematics of Operations Research 42, 330–348 (2017).
https:///doi.org/10.1287/moor.2016.0817

[12] Haihao Lu, Robert M. Freund és Jurij Neszterov, „Viszonylag sima konvex optimalizálás elsőrendű módszerekkel és alkalmazásokkal” SIAM Journal on Optimization 28, 333–354 (2018).
https:///doi.org/10.1137/16M1099546

[13] Marc Teboulle „Egyszerűsített nézet az elsőrendű optimalizálási módszerekről” Mathematical Programming 170, 67–96 (2018).
https://doi.org/10.1007/s10107-018-1284-2

[14] Masahito Hayashi „Bregman divergencián alapuló em-algoritmus és alkalmazása a klasszikus és kvantumsebességű torzításelméletben” IEEE Transactions on Information Theory 69, 3460–3492 (2023).
https:///doi.org/10.1109/tit.2023.3239955

[15] Masahito Hayashi „Iteratív minimalizálási algoritmus keverékcsaládon” (2023).
arXiv: 2302.06905

[16] Venkat Chandrasekaran és Parikshit Shah „Relatív entrópia optimalizálás és alkalmazásai” Mathematical Programming 161, 1–32 (2017).
https://doi.org/10.1007/s10107-016-0998-2

[17] Hamza Fawzi és Omar Fawzi „A kvantumrelatív entrópia hatékony optimalizálása” Journal of Physics A: Mathematical and Theoretical 51, 154003 (2018).
https:///doi.org/10.1088/1751-8121/aab285

[18] Hamza Fawzi, James Saunderson és Pablo A Parrilo, „Semidefinite approximations of the mátrix logathm” Foundations of Computational Mathematics 19, 259–296 (2019).
https://doi.org/10.1007/s10208-018-9385-0

[19] Chris Coey, Lea Kapelevich és Juan Pablo Vielma, „Teljesítményjavítások általános kúpos belső pont-algoritmushoz” Mathematical Programming Computation 15, 53–101 (2023).
https://doi.org/10.1007/s12532-022-00226-0

[20] Mehdi Karimiand Levent Tunçel „Primális–kettős belsőpontos módszerek tartományvezérelt formulációkhoz” Mathematics of Operations Research 45, 591–621 (2020).
https:///doi.org/10.1287/moor.2019.1003

[21] Mehdi Karimiand Levent Tuncel „Belsőpontos módszerek hatékony megvalósítása kvantumrelatív entrópiára” (2023).
arXiv: 2312.07438

[22] Lei Yangand Kim-Chuan Toh „A Bregman proximális pont algoritmusa újranézett: Új pontatlan változat és inerciális változata” SIAM Journal on Optimization 32, 1523–1554 (2022).
https:///doi.org/10.1137/20M1360748

[23] Nilanjana Datta, Min-Hsiu Hsieh, Mark M Wilde és Andreas Winter, „Quantum-to-classical Distortion Coding” Journal of Mathematical Physics 54 (2013).
https:///doi.org/10.1063/1.4798396

[24] Howard Barnum „Quantum rate-torzítás kódolása” Physical Review A 62, 042309 (2000).
https:///doi.org/10.1103/physreva.62.042309

[25] Zahra Baghali Khanian és Andreas Winter „A sebesség-torzítás perspektívája a kvantumállapotú újraelosztásról” (2021).
arXiv: 2112.11952

[26] Zahra Baghali Khanian, Kohdai Kuroiwa és Debbie Leung, „Sebesség-torzítás elmélete kevert állapotokhoz” 2023 IEEE International Symposium on Information Theory, 749–754 (2023).
https:///doi.org/10.1109/isit54713.2023.10206960

[27] Michael A. Nielsen és Isaac L. Chuang „Kvantumszámítás és kvantuminformáció: 10. évfordulós kiadás” Cambridge University Press (2010).
https:///doi.org/10.1017/cbo9780511976667

[28] Mark M. Wilde „Kvantuminformációs elmélet” Cambridge University Press (2017).
https:///doi.org/10.1017/9781316809976

[29] John Watrous „A kvantuminformáció elmélete” Cambridge University Press (2018).
https:///doi.org/10.1017/9781316848142

[30] R Tyrrell Rockafellar „Konvex elemzés” Princeton University Press (1970).
https:///doi.org/10.1007/bfb0110040

[31] Lev M Bregman „A konvex halmazok közös pontjának megtalálásának relaxációs módszere és alkalmazása a konvex programozási problémák megoldására” USSR Computational Mathematics and Mathematical Physics 7, 200–217 (1967).
https://doi.org/10.1016/0041-5553(67)90040-7

[32] Chris J Maddison, Daniel Paulin, Yee Whye Teh és Arnaud Doucet, „Dual space preconditioning for gradient descent” SIAM Journal on Optimization 31, 991–1016 (2021).
https:///doi.org/10.1137/19M130858X

[33] Dimitri Bertsekas „Konvex optimalizációs elmélet” Athena Scientific (2009).

[34] Theodor Bröckerand Tammo Tom Dieck „A kompakt hazugságcsoportok reprezentációi” Springer Science & Business Media (2013).
https://doi.org/10.1007/978-3-662-12918-0

[35] William Fultonand Joe Harris „Reprezentációs elmélet: Első tanfolyam” Springer Science & Business Media (2013).
https://doi.org/10.1007/978-1-4612-0979-9

[36] Glen E Bredon „Bevezetés a kompakt transzformációs csoportokba” Academic Press (1972).
https://doi.org/10.1016/s0079-8169(08)x6007-6

[37] Persi Diaconis és Steven Evans „Véletlen mátrixok sajátértékeinek lineáris funkcionálisai” Transactions of the American Mathematical Society 353, 2615–2633 (2001).
https://doi.org/10.1090/S0002-9947-01-02800-8

[38] Masahito Hayashi és Yuxiang Yang „Hatékony algoritmusok a kvantuminformáció szűk keresztmetszetére” Quantum 7, 936 (2023).
https://doi.org/10.22331/q-2023-03-02-936

[39] Stephen Boydand Lieven Vandenberghe „Konvex optimalizálás” Cambridge University Press (2004).
https:///doi.org/10.1017/cbo9780511804441

[40] Roger A. Hornand Charles R. Johnson „Témák a mátrixanalízisben” Cambridge University Press (1991).
https:///doi.org/10.1017/cbo9780511840371

[41] Mikhail V Solodovand Benar Fux Svaiter „Hibahatárok proximális pont-alproblémákhoz és a kapcsolódó pontatlan proximális pont-algoritmusokhoz” Mathematical Programming 88, 371–389 (2000).
https:///doi.org/10.1007/s101070050022

[42] Mark Schmidt, Nicolas Roux és Francis Bach, „Convergence rates of inexact proximális-gradiens method for convex optimization” Advances in Neural Information Processing Systems Proceedings of the 24th International Conference on Neural Information Processing Systems 24, 1458–1466 (2011).
https:///dl.acm.org/doi/10.5555/2986459.2986622

[43] Jorge Nocedaland Stephen J Wright „Numerikus optimalizálás” Springer (1999).
https:///doi.org/10.1007/b98874

[44] Nathaniel Johnston „QETLAB: A MATLAB eszköztár kvantum-összefonódáshoz, 0.9-es verzió” http:///qetlab.com (2016).
https:///doi.org/10.5281/zenodo.44637
http:///qetlab.com

[45] Kim-Chuan Toh, Michael J Todd és Reha H Tütüncü, „SDPT3 – A MATLAB szoftvercsomag félig meghatározott programozáshoz, 1.3-as verzió” Optimization Methods and Software 11, 545–581 (1999).
https:///doi.org/10.1080/10556789908805762

[46] Masahito Hayashi és Geng Liu „Általánosított kvantum Arimoto-Blahut algoritmus és alkalmazása a kvantuminformációs szűk keresztmetszetre” (2023).
arXiv: 2311.11188

[47] Thomas M. Coverand Joy A. Thomas „Az információelmélet elemei” John Wiley & Sons (1999).
https:///doi.org/10.1002/047174882X

[48] Aram V Arutyunovand Valeri Obukhovskii „Konvex és halmazértékű elemzés” De Gruyter (2017).
https:///doi.org/10.1515/9783110460308

[49] Martin Jaggi „Revisiting Frank-Wolfe: Projection-free sparse konvex optimalizálás” Proceedings of the 30th International Conference on International Conference on Machine Learning – Volume 28 427–435 (2013).
https:///dl.acm.org/doi/10.5555/3042817.3042867

[50] Haobo Liand Ning Cai „A Blahut-Arimoto típusú algoritmus a klasszikus kvantumcsatorna kapacitásának kiszámításához” International Symposium on Information Theory 2019 IEEE International Symposium on Information Theory 255–259 (2019).
https:///doi.org/10.1109/isit.2019.8849608

[51] Navneeth Ramakrishnan, Raban Iten, Volkher B Scholz és Mario Berta, „Computing quantum channel capacities” IEEE Transactions on Information Theory 67, 946–960 (2020).
https:///doi.org/10.1109/tit.2020.3034471

[52] Heinz H Bauschke és Jonathan M Borwein „Legendre-függvények és a véletlenszerű Bregman-projekciók módszere” Journal of Convex Analysis 4, 27–67 (1997).

[53] Rajendra Bhatia „Matrix elemzés” Springer Science & Business Media (2013).
https://doi.org/10.1007/978-1-4612-0653-8

Idézi

[1] Mehdi Karimi és Levent Tuncel, „Belső pont-módszerek hatékony megvalósítása kvantumrelatív entrópiához”, arXiv: 2312.07438, (2023).

[2] Masahito Hayashi és Geng Liu, „Általános kvantum Arimoto-Blahut algoritmus és alkalmazása a kvantuminformációs szűk keresztmetszetre”, arXiv: 2311.11188, (2023).

A fenti idézetek innen származnak SAO/NASA HIRDETÉSEK (utolsó sikeres frissítés: 2024-04-10 23:59:34). Előfordulhat, hogy a lista hiányos, mivel nem minden kiadó ad megfelelő és teljes hivatkozási adatokat.

On Crossref által idézett szolgáltatás művekre hivatkozó adat nem található (utolsó próbálkozás 2024-04-10 23:59:33).

Ez a tanulmány a Quantumban jelent meg Creative Commons Nevezd meg 4.0 International (CC BY 4.0) engedély. A szerzői jog az eredeti szerzői jog tulajdonosainál marad, például a szerzőknél vagy intézményeiknél.

SEO által támogatott tartalom és PR terjesztés. Erősödjön még ma.
PlatoData.Network Vertical Generative Ai. Erősítse meg magát. Hozzáférés itt.
PlatoAiStream. Web3 Intelligence. Felerősített tudás. Hozzáférés itt.
PlatoESG. Carbon, CleanTech, Energia, Környezet, Nap, Hulladékgazdálkodás. Hozzáférés itt.
PlatoHealth. Biotechnológiai és klinikai vizsgálatok intelligencia. Hozzáférés itt.
Forrás: https://quantum-journal.org/papers/q-2024-04-09-1314/

Időbélyeg: April 9, 2024

Időbélyeg: 21. március 2024.

Újra kiadta Platón

Absztrakt

Népszerű összefoglaló

► BibTeX adatok

► Referenciák

Idézi

A környezet használata a nem markovi nyílt kvantumrendszerek megértésére

Kvantizált nemlineáris transzport ultrahideg atomokkal

A kvantumkapcsolót az egységes műveletekre gyakorolt hatása egyedileg határozza meg

Kvantumkulcs-elosztási arányok félig meghatározott programozásból

Csak a klasszikus paraméterezett állapotok rendelkeznek optimális mérésekkel a legkisebb négyzetek vesztesége alatt

„Megfelelő” eltolási szabályok a zavart paraméteres kvantumevolúciók származékaihoz

Polinomiális függvények hatékony kvantumamplitúdó-kódolása

Fermion-qudit kvantumprocesszorok a rácsmérő elméletek anyaggal való szimulálására

A Converse a hibatűrő kvantumszámításhoz

Származtatott árképzés kvantumjelfeldolgozással

Rólunk

Vertical Search & Ai

Emelvény

Maradjon kapcsolatban

Fiók