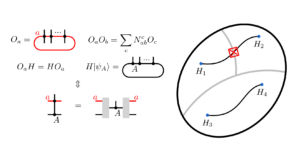Geometrikus operátori kvantumsebesség-korlát, Wegner-hamiltoni áramlás és a kezelő növekedése

Újra kiadta Platón

Követő: 0

Geometriai operátori kvantumsebesség-korlátozás, Wegner Hamiltoni áramlás és operátornövekedés PlatoBlockchain adatintelligencia. Függőleges keresés. Ai.

Niklas Hörnedal¹, Nicoletta Carabba¹, Kazutaka Takahashi^1,2és Adolfo del Campo^1,3

¹Fizikai és Anyagtudományi Tanszék, Luxemburgi Egyetem, L-1511 Luxembourg, GD Luxembourg
²Fizikai Műszaki Tanszék, Műszaki Kar, Mie Egyetem, Mie 514–8507, Japán
³Donostia Nemzetközi Fizikai Központ, E-20018 San Sebastián, Spanyolország

Érdekesnek találja ezt a cikket, vagy szeretne megvitatni? Scite vagy hagyjon megjegyzést a SciRate-en.

Absztrakt

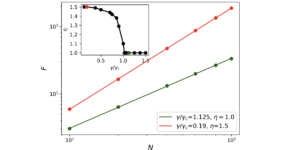
A kvantumsebesség-korlátok (QSL) alsó határokat adnak meg a folyamat kibontakozásához szükséges minimális időre azáltal, hogy a kvantumállapotok közötti távolságot használják, és meghatározzák az evolúció sebességét vagy annak felső korlátját. Bemutatjuk a QSL általánosítását, hogy jellemezzük egy általános operátor fejlődését, ha unitáriussal konjugálják. Az eredményül kapott QSL operátor (OQSL) megengedi a geometriai értelmezést, szűknek bizonyul, és tetszőleges unitáriusok, azaz idő- vagy paraméterfüggő generátorok által indukált operátorfolyamokra érvényes. A származtatott OQSL-t a Hamilton-féle renormalizációs csoportelmélet Wegner-áramlási egyenleteire és a Krylov-komplexitással számszerűsített operátornövekedésre alkalmazzuk.

► BibTeX adatok

@article{Hornedal2023geometricoperator, doi = {10.22331/q-2023-07-11-1055}, url = {https://doi.org/10.22331/q-2023-07-11-1055}, cím O}operátor {Q}uantum {S}peed {L}imit, {W}egner {H}amiltonia {F}low and {O}perator {G}rowth}, szerző = {H{“{o}}rnedal , Niklas és Carabba, Nicoletta és Takahashi, Kazutaka és del Campo, Adolfo}, folyóirat = {{Quantum}}, issn = {2521-327X}, kiadó = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, kötet = {7}, oldal = {1055}, hónap = júl, év = {2023} }

► Referenciák

[1] P. Pfeifer és J. Fröhlich, „Általános idő-energia bizonytalansági viszonyok és a rezonanciák élettartamának határai”, Rev. Mod. Phys. 67, 759-779 (1995).
https:///doi.org/10.1103/RevModPhys.67.759

[2] P. Busch, „The time-energy uncertainty relation”, Time in Quantum Mechanics, JG Muga, RS Mayato és Í. L. Egusquiza (Springer Berlin Heidelberg, Berlin, Heidelberg, 2008) 73–105.
https://doi.org/10.1007/978-3-540-73473-4_3

[3] LS Schulman: Jump time and passage time: The duration ofs a quantum transformation, Time in Quantum Mechanics, JG Muga, R. Sala Mayato és Í. L. Egusquiza (Springer Berlin Heidelberg, Berlin, Heidelberg, 2008) 107–128.
https://doi.org/10.1007/978-3-540-73473-4_4

[4] VV Dodonov és AV Dodonov, „Energia–idő és frekvencia–idő bizonytalansági viszonyok: pontos egyenlőtlenségek”, Physica Scripta 90, 074049 (2015).
https://doi.org/10.1088/0031-8949/90/7/074049

[5] L. Mandelstam és I. Tamm, „The uncertainty relation between energy and time in non-relativist quantum mechanics”, Selected Papers, szerkesztette Boris M. Bolotovskii, Victor Ya. Frenkel és Rudolf Peierls (Springer Berlin Heidelberg, Berlin, Heidelberg, 1991) 115–123.
https://doi.org/10.1007/978-3-642-74626-0_8

[6] S. Deffner és S. Campbell: „Kvantumsebesség-korlátok: a Heisenberg-féle bizonytalansági elvtől az optimális kvantumszabályozásig”, Journal of Physics A: Mathematical and Theoretical 50, 453001 (2017).
https://doi.org/10.1088/1751-8121/aa86c6

[7] Z. Gong és R. Hamazaki: „Bounds in nonequilibrium quantum dynamics”, International Journal of Modern Physics B 36, 2230007 (2022).
https:///doi.org/10.1142/S0217979222300079

[8] N. Margolus és LB Levitin, „A dinamikus evolúció maximális sebessége”, Physica D: Nonlinear Phenomena 120, 188–195 (1998), a Fourth Workshop on Physics and Consumption kiadványa.
https://doi.org/10.1016/S0167-2789(98)00054-2

[9] B. Zieliński és M. Zych, „Generalization of the margolus-levitin bound”, Phys. Rev. A 74, 034301 (2006).
https:///doi.org/10.1103/PhysRevA.74.034301

[10] N. Margolus, „A fizikai dinamika véges állapotú karaktere”, arXiv e-prints, arXiv:1109.4994 (2011), arXiv:1109.4994 [quant-ph].
arXiv: 1109.4994

[11] A. Uhlmann, „An Energy Dispersion becslés”, Physics Letters A 161, 329–331 (1992).
https://doi.org/10.1016/0375-9601(92)90555-Z

[12] S. Deffner és E. Lutz, „Energia–idő bizonytalanság reláció vezérelt kvantumrendszerekhez”, Journal of Physics A: Mathematical and Theoretical 46, 335302 (2013a).
https://doi.org/10.1088/1751-8113/46/33/335302

[13] M. Okuyama és M. Ohzeki: „Megjegyzés az „energia-idő bizonytalansági viszonyhoz vezérelt kvantumrendszerekhez””, Journal of Physics A: Mathematical and Theoretical 51, 318001 (2018a).
https:///doi.org/10.1088/1751-8121/aacb90

[14] MM Taddei, BM Escher, L. Davidovich és RL de Matos Filho, „Kvantum sebességkorlátozás fizikai folyamatokhoz”, Phys. Rev. Lett. 110, 050402 (2013).
https:///doi.org/10.1103/PhysRevLett.110.050402

[15] A. del Campo, IL Egusquiza, MB Plenio és SF Huelga, „Kvantum sebességkorlátozások a nyílt rendszer dinamikájában”, Phys. Rev. Lett. 110, 050403 (2013).
https:///doi.org/10.1103/PhysRevLett.110.050403

[16] S. Deffner és E. Lutz, „Quantum speed limit for non-markovian dynamics”, Phys. Rev. Lett. 111, 010402 (2013b).
https:///doi.org/10.1103/PhysRevLett.111.010402

[17] F. Campaioli, FA Pollock és K. Modi: „Szűk, robusztus és megvalósítható kvantumsebesség-korlátozások a nyitott dinamikához”, Quantum 3, 168 (2019).
https://doi.org/10.22331/q-2019-08-05-168

[18] LP García-Pintos és A. del Campo, „Kvantum sebességhatárok folyamatos kvantummérések alatt”, New Journal of Physics 21, 033012 (2019).
https:///doi.org/10.1088/1367-2630/ab099e

[19] B. Shanahan, A. Chenu, N. Margolus és A. del Campo, „Kvantum sebességhatárok a kvantum-klasszikus átmenetben”, Phys. Rev. Lett. 120, 070401 (2018).
https:///doi.org/10.1103/PhysRevLett.120.070401

[20] M. Okuyama és M. Ohzeki: „A kvantum sebességkorlátozás nem kvantum”, Phys. Rev. Lett. 120, 070402 (2018b).
https:///doi.org/10.1103/PhysRevLett.120.070402

[21] N. Shiraishi, K. Funo és K. Saito, „Sebességkorlátozás klasszikus sztochasztikus folyamatokhoz”, Phys. Rev. Lett. 121, 070601 (2018).
https:///doi.org/10.1103/PhysRevLett.121.070601

[22] SB Nicholson, LP García-Pintos, A. del Campo és JR Green, „Time-information uncertainty relations in thermodynamics”, Nature Physics 16, 1211–1215 (2020).
https:///doi.org/10.1038/s41567-020-0981-y

[23] VT Vo, T. Van Vu és Y. Hasegawa: „Egységes megközelítés a klasszikus sebességkorlátozáshoz és a termodinamikai bizonytalanság összefüggéséhez”, Phys. Rev. E 102, 062132 (2020).
https:///doi.org/10.1103/PhysRevE.102.062132

[24] T. Van Vu és Y. Hasegawa, „Az irreverzibilitás geometriai határai markovi rendszerekben”, Phys. Rev. Lett. 126, 010601 (2021).
https:///doi.org/10.1103/PhysRevLett.126.010601

[25] LP García-Pintos, SB Nicholson, JR Green, A. del Campo és AV Gorshkov, „Unifying quantum and classical speed limits on observables”, Phys. Rev. X 12, 011038 (2022).
https:///doi.org/10.1103/PhysRevX.12.011038

[26] I. Bengtsson és K. Życzkowski, Geometry of Quantum States: An Introduction to Quantum Entanglement, 2. kiadás. (Cambridge University Press, 2017).
https:///doi.org/10.1017/9781139207010

[27] DP Pires, M. Cianciaruso, LC Céleri, G. Adesso és DO Soares-Pinto, „Generalized geometric quantum speed limits”, Phys. Rev. X 6, 021031 (2016).
https:///doi.org/10.1103/PhysRevX.6.021031

[28] F. Campaioli, FA Pollock, FC Binder és K. Modi, „A kvantumsebesség-korlátozások szigorítása szinte minden államban”, Phys. Rev. Lett. 120, 060409 (2018).
https:///doi.org/10.1103/PhysRevLett.120.060409

[29] N. Hörnedal, D. Allan és O. Sönnerborn, „Extensions of the mandelstam–tamm quantum speed limit to systems in vegyes állapotú”, New Journal of Physics 24, 055004 (2022a).
https:///doi.org/10.1088/1367-2630/ac688a

[30] M. Bukov, D. Sels és A. Polkovnikov, „Geometric speed limit of accessible many-body statepreparation”, Phys. Rev. X 9, 011034 (2019).
https:///doi.org/10.1103/PhysRevX.9.011034

[31] T. Fogarty, S. Deffner, T. Busch és S. Campbell, „Orthogonality catastrophe as a result of the quantum speed limit”, Phys. Rev. Lett. 124, 110601 (2020).
https:///doi.org/10.1103/PhysRevLett.124.110601

[32] K. Suzuki és K. Takahashi: „Az adiabatikus kvantumszámítás teljesítményértékelése kvantumsebesség-korlátozásokon keresztül és lehetséges alkalmazások soktestű rendszerekben”, Phys. Rev. Research 2, 032016 (2020).
https:///doi.org/10.1103/PhysRevResearch.2.032016

[33] A. del Campo, „Kvantumsebesség-határok vizsgálata ultrahideg gázokkal”, Phys. Rev. Lett. 126, 180603 (2021).
https:///doi.org/10.1103/PhysRevLett.126.180603

[34] R. Hamazaki, „Makroszkópikus átmenetek sebességhatárai”, PRX Quantum 3, 020319 (2022).
https:///doi.org/10.1103/PRXQuantum.3.020319

[35] SL Braunstein, CM Caves és GJ Milburn, „Általános bizonytalansági viszonyok: elmélet, példák és lorentz-invariancia”, Annals of Physics 247, 135–173 (1996).
https:///doi.org/10.1006/aphy.1996.0040

[36] V. Giovannetti, S. Lloyd és L. Maccone, „Advances in quantum metrology”, Nature Photonics 5, 222–229 (2011).
https:///doi.org/10.1038/nphoton.2011.35

[37] G. Tóth és I. Apellaniz, „Quantum metrology from a quantum information science perspektíva”, Journal of Physics A: Mathematical and Theoretical 47, 424006 (2014).
https://doi.org/10.1088/1751-8113/47/42/424006

[38] M. Beau és A. del Campo, „Nonlinear quantum metrology of many-body open systems”, Phys. Rev. Lett. 119, 010403 (2017).
https:///doi.org/10.1103/PhysRevLett.119.010403

[39] T. Caneva, M. Murphy, T. Calarco, R. Fazio, S. Montangero, V. Giovannetti és GE Santoro, „Optimal control at the quantum speed limit”, Phys. Rev. Lett. 103, 240501 (2009).
https:///doi.org/10.1103/PhysRevLett.103.240501

[40] S. An, D. Lv, A. del Campo és K. Kim, „Shortcuts to adiabaticity by counterdiabatic drive for trapped-ion displacement in phase space”, Nature Communications 7, 12999 (2016).
https:///doi.org/10.1038/ncomms12999

[41] K. Funo, J.-N. Zhang, C. Chatou, K. Kim, M. Ueda és A. del Campo: „Universal work fluktuations during shortcuts to adiabaticity by counterdiabatic drive”, Phys. Rev. Lett. 118, 100602 (2017).
https:///doi.org/10.1103/PhysRevLett.118.100602

[42] S. Campbell és S. Deffner: „Trade-off a sebesség és a költség között az adiabaticitás rövidítésében”, Phys. Rev. Lett. 118, 100601 (2017).
https:///doi.org/10.1103/PhysRevLett.118.100601

[43] A. del Campo, J. Goold és M. Paternostro: „More bang for your buck: Super-adiabatic quantum engines”, Scientific Reports 4, 6208 (2014).
https:///doi.org/10.1038/srep06208

[44] FC Binder, S. Vinjanampathy, K. Modi és J. Goold, „Quantacell: hatékony kvantumelemek töltése”, New Journal of Physics 17, 075015 (2015).
https://doi.org/10.1088/1367-2630/17/7/075015

[45] F. Wegner: „Flow-equations for Hamiltonians”, Annalen der Physik 506, 77–91 (1994).
https:///doi.org/10.1002/andp.19945060203

[46] SD Głazek és KG Wilson, „Hamiltoniak renormalizálása”, Phys. Rev. D 48, 5863–5872 (1993).
https:///doi.org/10.1103/PhysRevD.48.5863

[47] SD Glazek és KG Wilson, „Perturbative renormalization group for Hamiltonians”, Phys. Rev. D 49, 4214–4218 (1994).
https:///doi.org/10.1103/PhysRevD.49.4214

[48] FJ Wegner: „Flow equations for Hamiltonians”, Physics Reports 348, 77–89 (2001).
https://doi.org/10.1016/S0370-1573(00)00136-8

[49] S. Kehrein, The Flow Equation Approach to Many-Particle Systems, Springer Tracts in Modern Physics (Springer Berlin Heidelberg, 2007).
https://doi.org/10.1007/3-540-34068-8

[50] CW von Keyserlingk, T. Rakovszky, F. Pollmann és SL Sondhi, „Operator hydrodynamics, otocs, and entanglement growth in systems without conservation laws”, Phys. Rev. X 8, 021013 (2018).
https:///doi.org/10.1103/PhysRevX.8.021013

[51] A. Nahum, S. Vijay és J. Haah, „Operator spreading in random unitary circles”, Phys. Rev. X 8, 021014 (2018).
https:///doi.org/10.1103/PhysRevX.8.021014

[52] T. Rakovszky, F. Pollmann és CW von Keyserlingk, „Diffusive hydrodynamics of out-of-time-ordered correlators with charge conservation”, Phys. Rev. X 8, 031058 (2018).
https:///doi.org/10.1103/PhysRevX.8.031058

[53] V. Khemani, A. Vishwanath és DA Huse: „Az operátorok terjedése és a disszipatív hidrodinamika megjelenése egységes evolúció során a megőrzési törvényekkel”, Phys. Rev. X 8, 031057 (2018).
https:///doi.org/10.1103/PhysRevX.8.031057

[54] DE Parker, X. Cao, A. Avdoshkin, T. Scaffidi és E. Altman, „A univerzális operátor növekedési hipotézis”, Phys. Rev. X 9, 041017 (2019).
https:///doi.org/10.1103/PhysRevX.9.041017

[55] D. Forster, Hidrodinamikai fluktuációk, törött szimmetria és korrelációs függvények, Advanced Books Classics (CRC Press, 2018).

[56] Nicoletta Carabba, Niklas Hörnedal és Adolfo del Campo, „Kvantum sebességkorlátozások a kezelői áramlásokra és a korrelációs függvényekre”, Quantum 6, 884 (2022).
https://doi.org/10.22331/q-2022-12-22-884

[57] B. Mohan és AK Pati, „Quantum speed limits for observables”, Phys. Rev. A 106, 042436 (2022).
https:///doi.org/10.1103/PhysRevA.106.042436

[58] JLF Barbón, E. Rabinovici, R. Shir és R. Sinha: „On the evolution of operator complexity after scrambling”, Journal of High Energy Physics 2019, 264 (2019).
https:///doi.org/10.1007/JHEP10(2019)264

[59] P. Caputa, JM Magan és D. Patramanis, „Geometry of krylov complexity”, Phys. Rev. Research 4, 013041 (2022).
https:///doi.org/10.1103/PhysRevResearch.4.013041

[60] Anatolij Dymarszkij és Alekszandr Gorszkij, „Kvantumkáosz mint delokalizáció a krilovi térben”, Phys. Rev. B 102, 085137 (2020).
https:///doi.org/10.1103/PhysRevB.102.085137

[61] E. Rabinovici, A. Sánchez-Garrido, R. Shir és J. Sonner: „Operator complexity: a travel to the edge of krylov space”, Journal of High Energy Physics 2021, 62 (2021).
https:///doi.org/10.1007/JHEP06(2021)062

[62] N. Hörnedal, N. Carabba, AS Matsoukas-Roubeas és A. del Campo, „Végső sebességhatárok a kezelői összetettség növekedéséhez”, Communications Physics 5, 207 (2022b).
https://doi.org/10.1038/s42005-022-00985-1

[63] H. Mori, „A Continued-Fraction Representation of the Time-Correlation Functions”, Progress of Theoretical Physics 34, 399–416 (1965).
https:///doi.org/10.1143/PTP.34.399

[64] R. Kubo, „The fluktuáció-disszipációs tétel”, Reports on Progress in Physics 29, 255 (1966).
https://doi.org/10.1088/0034-4885/29/1/306

[65] G. Müller V. S. Viswanath: A rekurziós módszer: Alkalmazás a sok test dinamikájára (Springer-Verlag, 1994).
https://doi.org/10.1007/978-3-540-48651-0

[66] R. R. Ernst, G. Bodenhausen és A. Wokaun: Principles of Nuclear Magnetic Resonance in One and Two Dimensions, Nemzetközi kémiamonográfiák sorozata (Clarendon Press, 1990).
https:///global.oup.com/academic/product/principles-of-nuclear-magnetic-resonance-in-one-and-two-dimensions-9780198556473

[67] JA Gyamfi, „A kvantummechanika alapjai a liouville-i térben”, European Journal of Physics 41, 063002 (2020).
https:///doi.org/10.1088/1361-6404/ab9fdd

[68] S. H. Friedberg, A. J. Insel és L. E. Spence, Lineáris algebra (Pearson, 2019).
https:///books.google.lu/books?id=zhw6vQEACAAJ

[69] LB Levitin és T. Toffoli: „A kvantumdinamika sebességének alapvető korlátja: Az egységes korlát szoros”, Phys. Rev. Lett. 103, 160502 (2009).
https:///doi.org/10.1103/PhysRevLett.103.160502

[70] J. Haegeman, TJ Osborne, H. Verschelde és F. Verstraete, „Entanglement renormalization for quantum fields in real space”, Phys. Rev. Lett. 110, 100402 (2013).
https:///doi.org/10.1103/PhysRevLett.110.100402

[71] M. Nozaki, S. Ryu és T. Takayanagi: „Holographic geometry of entanglement renormalization in quantum field theories”, Journal of High Energy Physics 2012, 193 (2012).
https:///doi.org/10.1007/JHEP10(2012)193

[72] J. Molina-Vilaplana és A. del Campo, „Complexity functions and bonyolultsági növekedési határok folyamatos mera áramkörökben”, Journal of High Energy Physics 2018, 12 (2018).
https:///doi.org/10.1007/JHEP08(2018)012

[73] P. Caputa, N. Kundu, M. Miyaji, T. Takayanagi és K. Watanabe, „Anti-de sitter space from optimization of path integrals in conformal field theories”, Phys. Rev. Lett. 119, 071602 (2017a).
https:///doi.org/10.1103/PhysRevLett.119.071602

[74] P. Caputa, N. Kundu, M. Miyaji, T. Takayanagi és K. Watanabe: „A Liouville-i cselekvés, mint útvonal-integrális komplexitás: a folyamatos tenzorhálózatoktól a hirdetésekig/cft”, Journal of High Energy Physics 2017, 97 ( 2017b).
https:///doi.org/10.1007/JHEP11(2017)097

[75] AR Brown, DA Roberts, L. Susskind, B. Swingle és Y. Zhao, „Complexity, action, and black holes”, Phys. Rev. D 93, 086006 (2016a).
https:///doi.org/10.1103/PhysRevD.93.086006

[76] AR Brown, DA Roberts, L. Susskind, B. Swingle és Y. Zhao: „A holografikus komplexitás egyenlő a tömeges akciókkal?” Phys. Rev. Lett. 116, 191301 (2016b).
https:///doi.org/10.1103/PhysRevLett.116.191301

[77] R. Uzdin és R. Kosloff, „Sebességkorlátozások a liouville-i térben nyílt kvantumrendszereknél”, EPL (Europhysics Letters) 115, 40003 (2016).
https://doi.org/10.1209/0295-5075/115/40003

[78] DA Lidar, A. Shabani és R. Alicki: „A szigorúan tisztaság-csökkentő kvantummarkoviandinamikának feltételei”, Chemical Physics 322, 82–86 (2006).
https:///doi.org/10.1016/j.chemphys.2005.06.038

[79] M. Toda, „Vibration of a chain with nonlinear interaction”, Journal of the Physical Society of Japan 22, 431–436 (1967a).
https:///doi.org/10.1143/JPSJ.22.431

[80] M. Toda, „Wave propagation in anharmonic lattices”, Journal of the Physical Society of Japan 23, 501–506 (1967b).
https:///doi.org/10.1143/JPSJ.23.501

[81] H. Flaschka: „A toda rács. ii. integrálok létezése”, Phys. Rev. B 9, 1924–1925 (1974).
https:///doi.org/10.1103/PhysRevB.9.1924

[82] J. Moser, Dinamikus rendszerek, elmélet és alkalmazások (Springer, 1975).
https://doi.org/10.1007/3-540-07171-7

[83] C. Monthus, „Flow to diagonalization for many-body-localization model: the adaptation of the toda mátrix differential flow to random kvantum spin chains”, Journal of Physics A: Mathematical and Theoretical 49, 305002 (2016).
https://doi.org/10.1088/1751-8113/49/30/305002

[84] M. Okuyama és K. Takahashi: „A klasszikus nemlineáris integrálható rendszerektől a kvantum-parancsikonokon át az adiabaticitásig”, Phys. Rev. Lett. 117, 070401 (2016).
https:///doi.org/10.1103/PhysRevLett.117.070401

[85] D. Chowdhury, A. Georges, O. Parcollet és S. Sachdev, „Sachdev-ye-kitaev modellek és azon túl: Ablak nem fermi folyadékokba”, Rev. Mod. Phys. 94, 035004 (2022).
https:///doi.org/10.1103/RevModPhys.94.035004

[86] S. Bravyi, DP DiVincenzo és D. Loss, „Schrieffer–wolff transzformáció kvantum-többtest-rendszerekhez”, Annals of Physics 326, 2793–2826 (2011).
https:///doi.org/10.1016/j.aop.2011.06.004

[87] L. D. Faddeev és L. A. Takhtajan, Hamiltoni módszerek a szolitonok elméletében (Springer, Berlin Heidelberg, 2007).
https://doi.org/10.1007/978-3-540-69969-9

[88] B. Sutherland, Gyönyörű modellek (World Scientific, 2004).
https:///doi.org/10.1142/5552

[89] DJ Gross, J. Kruthoff, A. Rolph és E. Shaghoulian, „$toverline{T}$ in ${mathrm{ads}}_{2}$ and quantum mechanics”, Phys. Rev. D 101, 026011 (2020a).
https:///doi.org/10.1103/PhysRevD.101.026011

[90] DJ Gross, J. Kruthoff, A. Rolph és E. Shaghoulian, „Hamiltoni deformációk a kvantummechanikában, $toverline{T}$ és a syk-modell”, Phys. Rev. D 102, 046019 (2020b).
https:///doi.org/10.1103/PhysRevD.102.046019

[91] AS Matsoukas-Roubeas, F. Roccati, J. Cornelius, Z. Xu, A. Chenu és A. del Campo, „Non-hermitian Hamilton-deformations in quantum mechanics” (2022).
https:///doi.org/10.48550/ARXIV.2211.05437

[92] Moody T. Chu és Kenneth R. Driessel: „A kivetített gradiens módszer a legkisebb négyzetek mátrix közelítéséhez spektrális megszorításokkal”, SIAM Journal on Numerical Analysis 27, 1050–1060 (1990).
http:///www.jstor.org/stable/2157698

[93] RW Brockett, „Dinamikus rendszerek, amelyek listákat rendeznek, mátrixokat diagonalizálnak és lineáris programozási problémákat oldanak meg”, Linear Algebra and its Applications 146, 79–91 (1991).
https://doi.org/10.1016/0024-3795(91)90021-N

[94] A. Bhattacharya, P. Nandy, PP Nath és H. Sahu: „Operator növekedés és krylov konstrukció disszipatív nyílt kvantumrendszerekben”, Journal of High Energy Physics 2022, 81 (2022).
https:///doi.org/10.1007/JHEP12(2022)081

[95] C. Liu, H. Tang és H. Zhai: „Krylov komplexitás nyílt kvantumrendszerekben” (2022).
https:///doi.org/10.48550/ARXIV.2207.13603

[96] Budhaditya Bhattacharjee, Xiangyu Cao, Pratik Nandy és Tanay Pathak: „Az operátor növekedési hipotézise nyílt kvantumrendszerekhez” (2022).
https:///doi.org/10.48550/ARXIV.2212.06180

Idézi

[1] Dimitrios Patramanis és Watse Sybesma, „Krylov komplexitás a Schrödinger algebra természetes alapjában”, arXiv: 2306.03133, (2023).

[2] Ryusuke Hamazaki, „Kvantumsebesség-határértékek többszörösen megfigyelhető anyagokhoz: megőrzési törvények, összefüggések és makroszkopikus rendszerek”, arXiv: 2305.03190, (2023).

[3] Pawel Caputa, Javier M. Magan, Dimitrios Patramanis és Erik Tonni, „Krylov komplexitás a moduláris Hamiltoni evolúcióban”, arXiv: 2306.14732, (2023).

A fenti idézetek innen származnak SAO/NASA HIRDETÉSEK (utolsó sikeres frissítés: 2023-07-11 23:44:31). Előfordulhat, hogy a lista hiányos, mivel nem minden kiadó ad megfelelő és teljes hivatkozási adatokat.

On Crossref által idézett szolgáltatás művekre hivatkozó adat nem található (utolsó próbálkozás 2023-07-11 23:44:29).

Ez a tanulmány a Quantumban jelent meg Creative Commons Nevezd meg 4.0 International (CC BY 4.0) engedély. A szerzői jog az eredeti szerzői jog tulajdonosainál marad, például a szerzőknél vagy intézményeiknél.

SEO által támogatott tartalom és PR terjesztés. Erősödjön még ma.
PlatoData.Network Vertical Generative Ai. Erősítse meg magát. Hozzáférés itt.
PlatoAiStream. Web3 Intelligence. Felerősített tudás. Hozzáférés itt.
PlatoESG. Autóipar / elektromos járművek, Carbon, CleanTech, Energia, Környezet, Nap, Hulladékgazdálkodás. Hozzáférés itt.
BlockOffsets. A környezetvédelmi ellentételezési tulajdon korszerűsítése. Hozzáférés itt.
Forrás: https://quantum-journal.org/papers/q-2023-07-11-1055/

Időbélyeg: Július 11, 2023

Időbélyeg: 6. július 2023.

Geometrikus kezelői kvantum sebességkorlát, Wegner Hamiltoni áramlás és a kezelő növekedése

Újra kiadta Platón

Absztrakt

► BibTeX adatok

► Referenciák

Idézi

Még több Quantum Journal

Kvantumszimuláció a félklasszikus rendszerben

A kritikus kvantumhőmérséklet és megvalósíthatósága spinrendszerekben

Metrológia és többrészes összefonódás a mérés által kiváltott fázisátalakulásban

Teljes kiterjesztése: a kvantumtisztítás nem jeladó analógja

Mátrixszorzat operátori szimmetriákkal védett fázisok osztályozása mátrixszorzatállapotok segítségével

A csapdába esett ionkvantumprocesszor koherens hibáinak jellemzése és enyhítése rejtett inverzek segítségével

Oszd meg és uralkodj ellenőrző módszer zajos, közepes léptékű kvantumszámításhoz

A kvantumkulcs-elosztás biztonsága az észlelési-hatékonysági eltéréssel többfoton esetén

Stabilizátorkódok számolása tetszőleges méretekhez

Rólunk

Vertical Search & Ai

Emelvény

Maradjon kapcsolatban

Fiók