1Matematikai Iskola, Bristoli Egyetem. n.linden@bristol.ac.uk
2QuSoft, CWI és Amszterdam Egyetem, Hollandia. rdewolf@cwi.nl
Érdekesnek találja ezt a cikket, vagy szeretne megvitatni? Scite vagy hagyjon megjegyzést a SciRate-en.
Absztrakt
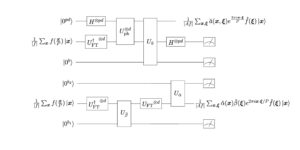
A kvantum-Fourier-transzformáció (QFT) a kvantumszámítás kulcsfontosságú primitívje, amelyet általában szubrutinként használnak egy nagyobb számításon belül, például fázisbecsléshez. Így előfordulhat, hogy kevés befolyásunk van a QFT-be bevitt állapot felett. Így egy jó QFT megvalósítása során elképzelhetjük, hogy jól kell teljesítenie tetszőleges bemeneti állapotokon. A QFT-implementáció legrosszabb esetben történő helyes viselkedésének $ellenőrzése$ általánosságban exponenciálisan nehéz lenne (a qubitek számában), ami felveti az aggodalmat, hogy ez az ellenőrzés a gyakorlatban lehetetlen bármilyen hasznos méretű rendszeren. Ebben a cikkben bemutatjuk, hogy valójában csak jó $átlag$-$eset$ teljesítményre van szükségünk a QFT-nek ahhoz, hogy jó $legrosszabb$-$eset$ teljesítményt érjünk el a kulcsfontosságú feladatokban – fázisbecslés, periódusmeghatározás és amplitúdóbecslés. . Ezen túlmenően egy nagyon hatékony eljárást adunk a QFT szükséges átlagos eset-viselkedésének ellenőrzésére.
Népszerű összefoglaló
► BibTeX adatok
► Referenciák
[1] Scott Aaronson és Patrick Rall. Kvantum közelítő számolás, egyszerűsítve. In Proceedings of 3rd Symposium on Simplicity in Algorithms (SOSA), 24–32. oldal, 2020. arXiv:1908.10846.
https:///doi.org/10.1137/1.9781611976014.5
arXiv: 1908.10846
[2] Charles H. Bennett, Ethan Bernstein, Gilles Brassard és Umesh Vazirani. A kvantumszámítás erősségei és gyengeségei. SIAM Journal on Computing, 26(5):1510–1523, 1997. quant-ph/9701001.
https:///doi.org/10.1137/S0097539796300933
arXiv:quant-ph/9701001
[3] Gilles Brassard, Peter Høyer, Michele Mosca és Alain Tapp. Kvantumamplitúdó-erősítés és becslés. In Quantum Computation and Quantum Information: A Millenium Volume, AMS Contemporary Mathematics Series 305. kötete, 53–74. oldal. 2002. quant-ph/0005055.
https:///doi.org/10.1090/conm/305/05215
arXiv:quant-ph/0005055
[4] Chi-Fang Chen és Fernando GSL Brandão. Koncentráció Trotter hibára. arXiv:2111.05324, 9. november 2021.
https:///doi.org/10.48550/arXiv.2111.05324
arXiv: 2111.05324
[5] Richard Cleve, Artur Ekert, Chiara Macchiavello és Michele Mosca. A kvantum algoritmusok újra áttekintése. In Proceedings of the Royal Society of London, A454. kötet, 339–354. oldal, 1998. quant-ph/9708016.
https:///doi.org/10.1098/rspa.1998.0164
arXiv:quant-ph/9708016
[6] Don Coppersmith. Egy közelítő Fourier-transzformáció, amely hasznos a kvantumfaktoringban. IBM Research Report No. RC19642, quant-ph/0201067, 1994.
https:///doi.org/10.48550/arXiv.quant-ph/0201067
arXiv:quant-ph/0201067
[7] Marcus da Silva, Oliver Landon-Cardinal és David Poulin. Kvantumkészülékek gyakorlati jellemzése tomográfia nélkül. Physical Review Letters, 107:210404, 2011. arXiv:1104.3835.
https:///doi.org/10.1103/PhysRevLett.107.210404
arXiv: 1104.3835
[8] Jens Eisert, Dominik Hangleiter, Nathan Walk, Ingo Roth, Damian Markham, Rhea Parekh, Ulysse Chabaud és Elham Kashefi. Kvantumtanúsítás és benchmarking. Nature Reviews Physics, 2:382–390, 2020. arXiv:1910.06343.
https://doi.org/10.1038/s42254-020-0186-4
arXiv: 1910.06343
[9] Steven T. Flammia és Yi-Kai Liu. Közvetlen hűségbecslés néhány Pauli-mérésből. Physical Review Letters, 106:230501, 2011. arXiv:1104.4695.
https:///doi.org/10.1103/PhysRevLett.106.230501
arXiv: 1104.4695
[10] András Gilyén, Srinivasan Arunachalam, and Nathan Wiebe. Kvantumoptimalizáló algoritmusok optimalizálása gyorsabb kvantumgradiens-számítással. In Proceedings of 30th ACM-SIAM SODA, 1425–1444, 2019. arXiv:1711.00465.
https:///doi.org/10.1137/1.9781611975482.87
arXiv: 1711.00465
[11] Lov K. Grover. Gyors kvantummechanikai algoritmus adatbázis-kereséshez. In Proceedings of 28th ACM STOC, 212–219. oldal, 1996. quant-ph/9605043.
https:///doi.org/10.1145/237814.237866
arXiv:quant-ph/9605043
[12] Gilyén András, Yuan Su, Guang Hao Low és Nathan Wiebe. Kvantum szinguláris érték transzformáció és azon túl: exponenciális fejlesztések a kvantummátrix aritmetikában. In Proceedings of 51st ACM STOC, 193–204. oldal, 2019. arXiv:1806.01838.
https:///doi.org/10.1145/3313276.3316366
arXiv: 1806.01838
[13] Stephen P. Jordan. Gyors kvantum algoritmus numerikus gradiens becsléshez. Physical Review Letters, 95:050501, 2005. quant-ph/0405146.
https:///doi.org/10.1103/PhysRevLett.95.050501
arXiv:quant-ph/0405146
[14] Alexey Yu. Kitaev. Kvantummérés és az Abeli-stabilizátor probléma. quant-ph/9511026, 12. november 1995.
https:///doi.org/10.48550/arXiv.quant-ph/9511026
arXiv:quant-ph/9511026
[15] Noah Linden és Ronald de Wolf. Kis számú nagy hiba könnyű detektálása kvantumáramkörben. Quantum, 5(436), 2021. arXiv:2009.08840.
https://doi.org/10.22331/q-2021-04-20-436
arXiv: 2009.08840
[16] Urmila Mahadev. Kvantumszámítások klasszikus verifikációja. In Proceedings of 59th IEEE FOCS, 259–267. oldal, 2018. arXiv:1804.01082.
https:///doi.org/10.1109/FOCS.2018.00033
arXiv: 1804.01082
[17] John M. Martyn, Zane M. Rossi, Andrew K. Tan és Isaac L. Chuang. A kvantumalgoritmusok nagyszerű egyesítése. PRX Quantum, 2:040203, 2021. arXiv.2105.02859.
https:///doi.org/10.1103/PRXQuantum.2.040203
[18] Michael A. Nielsen és Isaac L. Chuang. Kvantumszámítás és kvantuminformáció. Cambridge University Press, 2000.
https:///doi.org/10.1017/CBO9780511976667
[19] Patrick Rall. Gyorsabb koherens kvantum-algoritmusok fázis-, energia- és amplitúdóbecsléshez. Quantum, 5(566), 2021. arXiv:2103.09717.
https://doi.org/10.22331/q-2021-10-19-566
arXiv: 2103.09717
[20] Peter W. Shor. Polinom idejű algoritmusok prímfaktorizáláshoz és diszkrét logaritmusokhoz kvantumszámítógépen. SIAM Journal on Computing, 26(5):1484–1509, 1997. Korábbi verzió a FOCS'94-ben. quant-ph/9508027.
https:///doi.org/10.1137/S0097539795293172
arXiv:quant-ph/9508027
[21] Qi Zhao, You Zhou, Alexander F. Shaw, Tongyang Li és Andrew M. Childs. Hamiltoni szimuláció véletlenszerű bemenetekkel. arXiv:2111.04773, 8. november 2021.
https:///doi.org/10.48550/arXiv.2111.04773
arXiv: 2111.04773
Idézi
[1] Joran van Apeldoorn, Arjan Cornelissen, Gilyén András és Giacomo Nannicini, „Quantum tomography using state-preparation unities”, arXiv: 2207.08800.
A fenti idézetek innen származnak SAO/NASA HIRDETÉSEK (utolsó sikeres frissítés: 2022-12-08 04:24:57). Előfordulhat, hogy a lista hiányos, mivel nem minden kiadó ad megfelelő és teljes hivatkozási adatokat.
On Crossref által idézett szolgáltatás művekre hivatkozó adat nem található (utolsó próbálkozás 2022-12-08 04:24:56).
Ez a tanulmány a Quantumban jelent meg Creative Commons Nevezd meg 4.0 International (CC BY 4.0) engedély. A szerzői jog az eredeti szerzői jog tulajdonosainál marad, például a szerzőknél vagy intézményeiknél.