הוכחה מפתיעה למדעי המחשב מהממת מתמטיקאים

ביום ראשון, 5 בפברואר, קיבלו אולוף סיססק ותומס בלום אימייל המכיל פריצת דרך מהממת על הבעיה הכי לא פתורה בתחומם. זנדר קלי, סטודנט לתואר שני באוניברסיטת אילינוי, אורבנה-שמפיין, שלח את סיססק ובלום מאמר שהוא כתב עם Raghu Meka מאוניברסיטת קליפורניה, לוס אנג'לס. גם קלי וגם מקה היו מדעני מחשב, עולם אינטלקטואלי מלבד הקומבינטוריקה התוספות שסיססק ובלום חוקרים.

"המוח שלי פשוט התפוצץ. כאילו, רגע, הם באמת עשו את זה?" אמר סיססק, מרצה באוניברסיטת שטוקהולם. קלי ומקה, מבחוץ לתחום הקומבינטוריקה, אמרו שהם מצאו גבול חדש - ונמוך באופן דרמטי - לגודל של קבוצה של מספרים שלמים שבהם אין שלושה מהם מרווחים באופן שווה (שוללים שילובים כמו 3, 8 ו-13 או 101, 201 ו-301).

הטענה של קלי ומקה ריסקה את השיא הקודם, הושג בשנת 2020 מאת סיסאסק ובלום, שהוא עמית מחקר באוניברסיטת אוקספורד. "העבודה של בלום וסיססק - עבודה חזקה מאוד שזה היה - זה באמת נתן רושם של סופר קשה לשפר אותה", אמר בן גרין, עמיתו של בלום באוקספורד. "זה נראה מאוד תקוע איפה זה היה."

למרות שגם לבלום וגם לסיססק היו עניינים דחופים אחרים לטפל בהם בזמן שהם קיבלו את המייל - בלום זה עתה אימצה גור, בעוד שסיססק היה באמצע המעבר - הם החלו במהירות לעבוד על אימות העיתון החדש.

בתוך ימים, בלום וסיססק היו משוכנעים שההוכחה החדשה נכונה. סיססק כינה זאת "התוצאה הגדולה ביותר באזור זה 20 שנה". להוטים שאחרים יעריכו את הרעיונות של קלי ומקה, הם ניסחו דו"ח להסביר את ההוכחה במונחים המוכרים יותר למתמטיקאים.

מקה אמר כי התגובה מהקהילה "הייתה חיובית יותר ממה שחשבתי. מדהים לראות את כל התגובות".

התקדמות ממושכת

הרצפים של מספרים ברווח שווה שקלי ומקה ביקשו להימנע מהם נקראים התקדמות אריתמטית. הם יכולים להימשך לנצח או להכיל רק כמה מונחים. קלי ומקה התמקדו בהתקדמות שהורכבו משלושה מספרים בלבד, בעקבות שורת מחקר שמקורה לעתים קרובות ב- נייר 1936 מאת פול ארדס ופול טוראן.

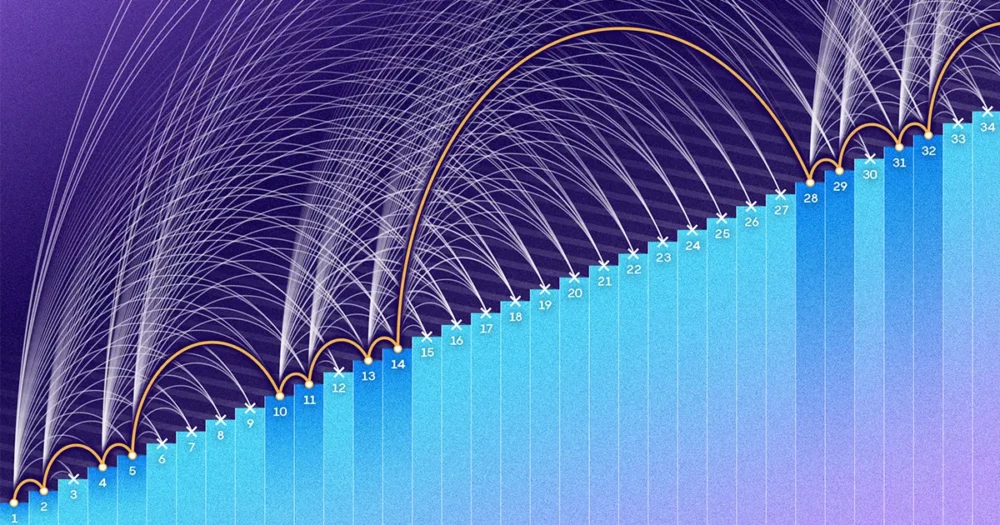
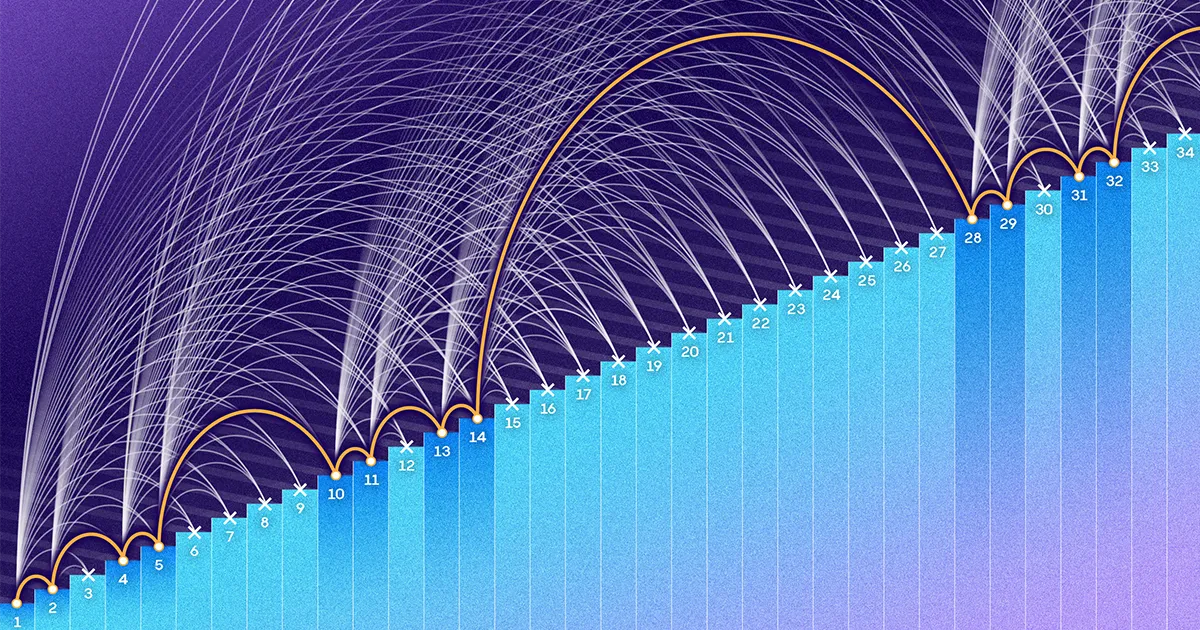
ארדס וטוראן רצו לדעת כמה מספרים קטנים מתקרה כלשהי N ניתן להכניס לסט מבלי ליצור התקדמות אריתמטית של שלושה טווחים. N יכול להיות 1,000, 1 מיליון, או מספר עצום בלתי נתפס. הם שיערו שכן N גדל, קבוצה ללא התקדמות של שלוש טווחים תצטרך להיות דלילה להפליא. יצירת סט כזה יהיה כמו איסוף נעליים תוך התעקשות שאין שני זוגות באותו צבע. אולי תוכל להמשיך לנצח, אבל ככל שהאוסף שלך גדל, תמצא את עצמך מוסיף לו בקצב איטי יותר ויותר.

"יש איזשהו מבנה שהולך לצוץ לתוך הסט, לא משנה איך בחרת את הסט," הסביר מקה. "כמה סט גדול אתה באמת צריך כדי להבטיח שיש לך את המבנה הזה שם?"

בשנת 1946, פליקס ברנד מצאו דרך לבנות סטים של מספרים בין 1 ל N מבלי לייצר התקדמות תלת טווח. השיטה שלו הביאה לסטים שגדלו כמו N עשה, אבל לאט כואב. מתי N הוא 100,000, הסט של Behrend מכיל רק 171 אלמנטים. מתי N הוא 1 מיליון, לקבוצה שלו יש 586 מספרים - פחות מ-0.06% מהמספרים שבין 1 ל-1 מיליון.

הקבוצות של ברנד נתנו למתמטיקאים קומה לעבוד איתה: הסט הגדול ביותר ללא התקדמות של שלוש טווחים יצטרך להיות גדול לפחות כמו של ברנד. בשנת 1953, קלאוס רוט סיפק תקרה, מציאת עבר סף שקבוצה חייבת בהכרח להכיל התקדמות של שלושה טווחים.

רוט הוכיח את ההשערה של ארדוס וטוראן בכך שהראה זאת N גדל, סט ללא התקדמות שלוש טווח יהווה חלק קטן יותר ויותר מהמספרים בין 1 ל-N. אבל התקרה של רוט הייתה רחוקה מהקומה של ברנד. Behrend הראה ש-0.06% מהאלמנטים שבין 1 ל-1 מיליון יכולים להיכנס לסט ללא התקדמות. למרות שקשה לחשב את הנוסחה של רוט במדויק, היא לא מתקרבת כל כך נמוכה - הערכה גסה אחת מגדירה את האחוז בכ-40%.

אבל יותר בולט מהפער המסוים הזה היה ההתנהגות הכוללת של שתי הנוסחאות. צייר את שבריר האלמנטים בין 1 ל N שכל נוסחה מייצגת, ותראה את המספר של Behrend מתכווץ במהירות לאפס כ N גדל. השבר של רוט, לעומת זאת, מחליק לעבר האפס, אבל לאט ובעדינות. שתי העקומות הן צורות שונות מאוד, והשיעור האמיתי של יסודות השוכבים בקבוצה ללא התקדמות אריתמטית יכול, עד כמה שידעו המתמטיקאים, להיות בכל מקום ביניהם.

החל משנות השמונים, "היה רצף ארוך של, בדיעבד, שיפורים מצטברים למדי על ידי מספר רב של מתמטיקאים מפורסמים באמת", אמר גרין. מדי פעם מישהו היה דוחף את הגבול העליון של רוט בשערה או שתיים, ובסופו של דבר הוא ירד במידה ניכרת. הגבול התחתון של ברנד, לעומת זאת, לא זז במשך עשרות שנים. מתמטיקאים החלו לחשוב שאולי ברנד לא היה רחוק מהתשובה האמיתית, אמר בלום.

עד שהגיע המאמר של קלי ומקה בתחילת 2023, הגודל המקסימלי של סט ללא התקדמות נכתב מלמטה על ידי הנוסחה של ברנד, ומלמעלה על ידי בלום וסיססק. המאמר של בלום וסיססק מיולי 2020 חצה את הסף ה"לוגריתמי" הקריטי בכך שהראה שסט ללא התקדמות חייב להכיל פחות מ- N/(עֵץ N) אלמנטים. אבל התוצאה שלהם עדיין הייתה גבוה מעל זו של בהרנד. הגבול העליון החדש של קלי ומקה קרוב יותר באופן דרסטי לקומה שנקבעה על ידי Behrend.

"מקה וקלי די קפצו על כל ההתקדמות המצטברת הזו", אמר טרנס טאו, מתמטיקאי בולט ב-UCLA.

הנוסחה שלהם כמעט זהה לזו של Behrend, עם רק כמה פרמטרים מותאמים. כפי ש N מתקרב לאינסוף, עלילה של הנוסחה של קלי ומקה תתייצב בסופו של דבר בעקומה הדומה לעקומת Behrend. "כל חיבור של הצורה הזו פשוט נראה כמו חלום בלתי אפשרי לפני כן", אמר בלום.

"באמת הייתי די המום מכך שהם עשו שיפור כזה", אמר גרין.

טאק שונה

 למרות שקלי ומקה מעולם לא העזו לחלוטין את מחקר המתמטיקה הטהור לפני כן, התקדמות אריתמטית היו מוכרות להם כשהם התחילו. באופן כללי, מדעני מחשבים "מסתכלים ברעב כלפי חוץ אחר טכניקות שיעבדו כדי לפתור את הבעיות שלנו", אמרה קלי. הכלים ששימשו בעבר לחקר הגודל של קבוצה ללא התקדמות הפכו בשימוש נרחב בתת-תחום מדעי המחשב של תורת המורכבות. הבעיה של צמצום הגודל של קבוצה כזו מוכרת היטב לתיאורטיקנים של מורכבות כדוגמה מובהקת ליישום טכניקות הבודקות את המבנה הפנימי של קבוצות.

בסוף 2021, קלי ומקה ניתחו את הסיכויים שצוות שחקנים במשחק שיתופי מסוים יוכל לנצח, סוג סטנדרטי של בעיה במדעי המחשב. עלה בדעתם שטכניקות ממחקר על הגודל של סטים ללא התקדמות עשויות להיות מועילות. אבל הם מצאו שקל יותר ללמוד ישירות את הטכניקות האלה מאשר ליישם אותן במשחק השיתופי. "הרעיון הטוב ביותר שלי כיצד להתקדם בבעיה זו [היה] למעשה לשפר את הכלי עצמו, לא להשתמש בו בצורה חכמה יותר", אמרה קלי.

"בשלב מסוים, פשוט החלטנו לעבוד על השאלה הזו ישירות", נזכר מקה. שישה חודשים לאחר מכן, שני החוקרים הבינו את האסטרטגיה שלהם ורק היו צריכים לברר כיצד ליישם את השיטה שלהם על הבעיה שעל הפרק.

כדי לראות איך הם הגיעו לגבול העליון החדש שלהם, קח כל קבוצה של מספרים בין 1 ל- N. קורא לזה A. הצפיפות של A הוא אחוז המספרים בין 1 ל N שזה כולל. מכיוון שיש הרבה התקדמות אריתמטית אפשרית בין 1 ל N, אם לא תבחר את האלמנטים של A בזהירות, כל A עם צפיפות גבוהה ככל הנראה יכיל הרבה התקדמות אריתמטית.

בהוכחה שלהם, קלי ומקה דמיינו זאת A היו מעט או ללא התקדמות אריתמטית, והם ניסו לאתר את ההשלכות. אם A היה צפוף מספיק, הם הראו שהיעדר התקדמות מחייב רמת מבנה בפנים A זה יביא בהכרח לסתירה, כלומר A חייב, אחרי הכל, להכיל לפחות התקדמות אחת.

כדי להבין את המבנה הזה, הם שקלו את הסט A + A, המורכב מכל המספרים שנוצרו על ידי הוספת שני אלמנטים של A. הם שמו לב שאם A מכיל התקדמות אריתמטית מעטה יחסית, הדבר מרמז על יתירות בין המרכיבים של A + A: זוגות שונים של מספרים מ A לעתים קרובות מסתכמים לאותו מספר.

ניתן להגדיר צפיפות לא רק בהשוואה לכל המספרים השלמים בין 1 ל N אבל בהשוואה לתת-קבוצה כלשהי - אמור רק את המספרים השלמים הזוגיים במרווח הזה, או רק את הכפולות של 3. קלי ומקה השתמשו ביתירות ב A + A למצוא תת-קבוצה של המספרים השלמים שבהם אלמנטים של A היו נפוצים במיוחד.

אם A הכיל כפולות של 3 בצורה לא פרופורציונלית, למשל, קלי ומקה היו מתמקדים בחלק שכלל כפולות של 3. הם חזרו על האסטרטגיה הזו שוב ושוב. בכל פעם הם מצאו תת-קבוצות קטנות יותר ויותר של המספרים השלמים, מעליהם Aהצפיפות של תמשיך לגדול ולגדול. לדוגמה, A עשוי להכיל 10% מהמספרים השלמים בין 1 ל N, 15% מהמכפילות של 3 במרווח זה, ו-25% מהכפולות הזוגיות של 3.

משהו מעניין קורה כאשר A זה גדול. אם ההליך חוזר על עצמו, הצפיפות של A על תת-קבוצה כלשהי עולה על 100%. זה, כמובן, בלתי אפשרי. A יכול להכיל, נניח, את כל הכפולות של 24, אבל הוא לא יכול להכיל יותר מכולם. הפרדוקס הזה מתעורר רק אם A גדול מספיק מלכתחילה, אבל כשזה קורה, זה אומר ההנחה ש A אינו מכיל התקדמות אריתמטית ודאי הייתה שגויה.

זה "טיעון מנצח", מתי A הוא גדול, אמרה מקה. אוֹ A כולל הרבה התקדמות אריתמטית, או שיש הרבה יתירות A + A - במקרה זה הם יכולים להשתמש בהליך מציאת המשנה (שנקרא "אסטרטגיית הגדלת הצפיפות") כדי להראות שהתקדמות חייבת להופיע ב A. למרות שאסטרטגיית הגדלת הצפיפות היא תוכנית שחוקה היטב בשטח, קלי ומקה הצליחו לגרום לזה לעבוד עבור קטנים יותר Aזה מאי פעם. עם זה, הם חשפו תקרה חדשה בגודל של סט ללא התקדמות.

קלי ומקה בנו שילוב ייחודי של רעיונות מתוך תוכנית תוספת הצפיפות. במקום להמציא מסגרת חדשה לגמרי, הם חשבו מחדש על הדרך שבה הם מצאו את המשנה הצפופה שלהם. לשם כך, הם השתמשו בטכניקה שהם כינו "ניפוי", אשר מורכבת מהסטת הסט שלהם בכמות קבועה, חצייתו עם עצמו וחזרה על התהליך פעמים רבות. מה שנשאר, לאחר סבבים רבים של צומת, הוא סט מובנה מאוד עם מאפיינים צפויים. אף על פי שנעשה שימוש בניפוי במאמרים אחרים, היא מעולם לא נוסתה על בעיית ההתקדמות של שלושת המועדים.

במבט לאחור

קלי ומקה הורידו את מגבלת הגודל של סט ללא התקדמות בכמות מזעזעת על ידי הזרקת כלים מוזנחים כמו ניפוי לשיטות מסורתיות. "קלי ומקה הראו לנו שאיכשהו הטכניקות האלה, שישבו שם בשטח פתוח, היו פשוט הרבה יותר חזקות ממה שחשדנו", אמר בלום. לאור היעילות החדשה של הכלים הללו, הוא הוסיף, "עלינו לחזור ולבדוק הכל מחדש".

אסטרטגיית הגדלת הצפיפות הופיעה לראשונה במאמרו של רוט לפני 70 שנה ומאז נעשה שימוש ברוב המאמרים על התקדמות אריתמטית. גרין הופתע מכך שניתן להשתמש במסגרת המסגרת כדי להוכיח גבול נמוך כמו של קלי ומקה. "חשבתי שיהיה צורך במשהו שונה לחלוטין, באופן קיצוני", אמר.

קלי נרגש להמשיך את הגיחה שלו למתמטיקה. "לא חסר לי תקוות וחלומות על הרבה בעיות שונות שלפחות אחשוב על קשר רוחני לזה", אמר.

העובדה שקלי ומקה הצליחו לזהות את כוחם של רעיונות שפעם התעלמו מהם מראה את האופי הפוגעני של התקדמות מתמטית - תכונה שבעיני טאו היא יותר ברכה מאשר קללה. "לא תמיד מתמטיקה רק הופכת קשה יותר ויותר", אמר. "תודה לאל."