ב1850, תומס פנינגטון קירקמן, מתמטיקאי כשלא מילא את אחריותו העיקרית ככונן בכנסייה האנגלית, תיאר את "בעיית תלמידות בית הספר" שלו: "חמש עשרה נשים צעירות בבית ספר יוצאות שלוש לידן במשך שבעה ימים ברציפות: זה נדרש לארגן אותם מדי יום, כדי שלא ילכו שניים לצדם פעמיים."
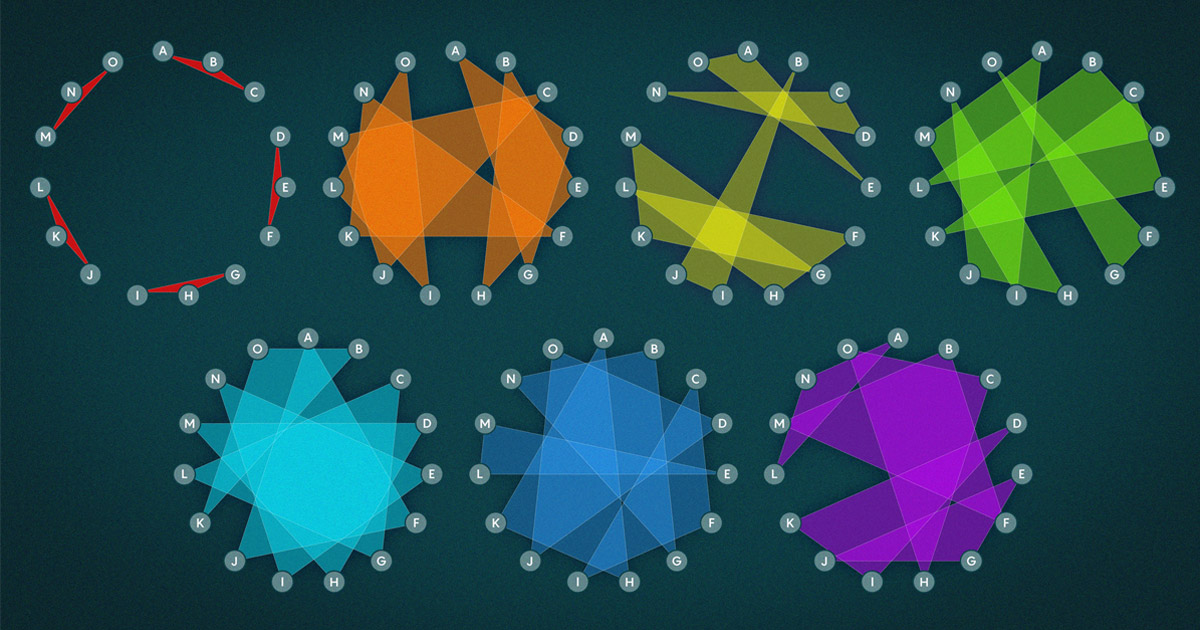
למתמטיקאי מודרני, בעיה מסוג זה היא הטובה ביותר לדמיין כהיפרגרף - קבוצה של צמתים שנאספו בקבוצות של שלושה או יותר. 15 תלמידות בית הספר הן צמתים, וניתן לחשוב על כל קבוצה של "שלושה צמודים" כמשולש, עם שלושה קווים, או קצוות, המחברים שלושה צמתים.
הבעיה של קירקמן בעצם שואלת אם יש סידור של המשולשים האלה שמחבר את כל תלמידות בית הספר זו לזו, אבל עם ההגבלה הנוספת שאין שני משולשים חולקים קצה. שיתוף קצה ירמז ששתי תלמידות בית ספר צריכות ללכת יחד יותר מפעם אחת. הגבלה זו פירושה שכל בחורה מטיילת עם שני חברים חדשים כל יום במשך שבוע, כך שכל זוג אפשרי מתכנס בדיוק פעם אחת.
בעיה זו ואחרות דומות לה הפתיעו מתמטיקאים במשך כמעט מאתיים השנים מאז שאל קירקמן את שאלתו. בשנת 1973, המתמטיקאי האגדי פול ארדס הציג דמות דומה. הוא שאל אם אפשר לבנות היפרגרף עם שני מאפיינים שלכאורה אינם תואמים. ראשית, כל זוג צמתים חייב להיות מחובר במשולש אחד בדיוק, כמו אצל תלמידות בית הספר. תכונה זו הופכת את הגרף לצפוף במשולשים. הדרישה השנייה מאלצת את המשולשים להתפרס בצורה מאוד מדויקת. (באופן ספציפי, זה מחייב שלכל קבוצה קטנה של משולשים, יש לפחות שלושה צמתים יותר מאשר יש משולשים.) "יש לך התנהגות מעט סותרת זו שבה יש לך אובייקט כולל צפוף שאין לו חלקים צפופים," אמר. דיוויד קונלון, מתמטיקאי במכון הטכנולוגי של קליפורניה.
בינואר הקרוב, ב הוכחה מורכבת של 50 עמודים, ארבעה מתמטיקאים הוכיחו שתמיד אפשר לבנות היפרגרף כזה כל עוד יש לך מספיק צמתים. "כמות הטכניות שעברו [הם] רק כדי לקבל את זה, זה היה מדהים", אמר אלן לו, מתמטיקאי באוניברסיטת ברמינגהם. קונלון הסכים: "זו יצירה ממש מרשימה".
צוות המחקר בנה מערכת שעמדה בדרישות השטניות של Erdős על ידי התחלת תהליך אקראי לבחירת משולשים והנדסת אותו בקפידה יתרה כדי להתאים לצרכיהם. "מספר השינויים הקשים שנכנסים להוכחה הוא למעשה די מדהים", אמר קונלון.
האסטרטגיה שלהם הייתה לבנות בזהירות את ההיפרגרף ממשולשים בודדים. לדוגמה, דמיינו את 15 תלמידות בית הספר שלנו. צייר קו בין כל זוג.
המטרה כאן היא לאתר משולשים על גבי קווים אלו כך שהמשולשים יעמדו בשתי דרישות: ראשית, אין שני משולשים חולקים קצה. (מערכות הממלאות את הדרישה הזו נקראות מערכות משולשות של שטיינר.) ושנית, ודא שכל תת-קבוצה קטנה של משולשים מנצלת מספר גדול מספיק של צמתים.
הדרך שבה החוקרים עשו זאת מובן אולי בצורה הטובה ביותר עם אנלוגיה.
תגיד שבמקום לעשות משולשים מקצוות, אתה בונה בתים מלבני לגו. הבניינים הראשונים שאתה עושה הם אקסטרווגנטיים, עם חיזוקים מבניים וקישוטים משוכללים. לאחר שתסיים עם אלה, הנח אותם בצד. הם ישמשו כ"סופג" - סוג של מאגר מובנה.
עכשיו התחל ליצור בניינים מהלבנים שנותרו שלך, המשך בלי הרבה תכנון. כאשר מלאי הלגו שלך מתדלדל, אתה עלול למצוא את עצמך עם כמה לבנים תועים, או בתים שאינם תקינים מבחינה מבנית. אבל מכיוון שמבני הבולמים כל כך מוגזמים ומחוזקים, אתה יכול לקטוף כמה לבנים פה ושם ולהשתמש בהם בלי לחזר אחרי קטסטרופה.
במקרה של מערכת המשולשת שטיינר, אתה מנסה ליצור משולשים. הבולם שלך, במקרה זה, הוא אוסף קצוות שנבחר בקפידה. אם אתה מוצא את עצמך לא מסוגל למיין את שאר המערכת למשולשים, אתה יכול להשתמש בחלק מהקצוות המובילים לתוך הבולם. ואז, כשתסיים לעשות את זה, אתה מפרק את הבולם עצמו למשולשים.
קליטה לא תמיד עובדת. אבל מתמטיקאים התעסקו בתהליך, ומצאו דרכים חדשות לסמור סביב מכשולים. לדוגמה, גרסה רבת עוצמה הנקראת ספיגה איטרטיבית מחלקת את הקצוות לרצף מקונן של קבוצות, כך שכל אחת מהן פועלת כסופגת עבור הבא הגדול ביותר.
"בעשור האחרון בערך חלו שיפורים מסיביים", אמר קונלון. "זה סוג של אמנות, אבל הם באמת נשאו את זה לרמה של אמנות גבוהה בשלב זה."
הבעיה של Erdős הייתה מסובכת אפילו עם ספיגה איטרטיבית. "די מהר התברר מדוע הבעיה הזו לא נפתרה", אמר מהטאב סווני, אחד מארבעת החוקרים שפתרו אותה, יחד עם אשווין סאה, שיחד עם סווני הוא סטודנט לתואר שני במכון הטכנולוגי של מסצ'וסטס; מיכאל סימקין, פוסט-דוקטורט במרכז למדעים ויישומים מתמטיים באוניברסיטת הרווארד; ו מתיו קוואן, מתמטיקאי במכון למדע וטכנולוגיה אוסטריה. "היו משימות טכניות די מעניינות, די קשות."
לדוגמה, ביישומים אחרים של קליטה איטרטיבית, ברגע שאתה מסיים לכסות קבוצה - או עם משולשים, עבור מערכות משולשות של שטיינר, או עם מבנים אחרים לבעיות אחרות - אתה יכול לשקול את זה מטופל ולשכוח מזה. עם זאת, התנאים של Erdős מנעו מארבעת המתמטיקאים לעשות זאת. מקבץ בעייתי של משולשים יכול בקלות לכלול צמתים ממספר ערכות בולמים.
"משולש שבחרת לפני 500 צעדים, אתה צריך איכשהו לזכור איך לחשוב על זה," אמר סווני.
מה שהארבעה הבינו בסופו של דבר זה שאם הם יבחרו את המשולשים שלהם בקפידה, הם יוכלו לעקוף את הצורך לעקוב אחר כל דבר קטן. "מה שעדיף לעשות זה לחשוב על כל קבוצה קטנה של 100 משולשים ולהבטיח שקבוצת משולשים נבחרת עם ההסתברות הנכונה", אמר סווני.
מחברי המאמר החדש אופטימיים שניתן להרחיב את הטכניקה שלהם מעבר לבעיה אחת זו. יש להם כבר יישמו את האסטרטגיה שלהם לבעיה לגבי ריבועים לטיניים, שהם כמו פישוט של חידת סודוקו.
מעבר לכך, ישנן מספר שאלות שעשויות להניב בסופו של דבר לשיטות הקליטה, אמר קוואן. "יש כל כך הרבה בעיות בקומבינטוריקה, במיוחד בתורת העיצוב, שבה תהליכים אקראיים הם כלי רב עוצמה." בעיה אחת כזו, השערת Ryser-Brualdi-Stein, עוסקת גם בריבועים לטיניים וחיכתה לפתרון מאז שנות ה-1960.
למרות שקליטה עשויה להזדקק לפיתוח נוסף לפני שהיא תוכל להיפטר מהבעיה הזו, היא עברה כברת דרך מאז הקמתה לפני 30. מאיה שטיין, סגן מנהל המרכז למידול מתמטי באוניברסיטת צ'ילה. "זה משהו שבאמת נהדר לראות, איך השיטות האלה מתפתחות."