1ICFO-Institut de Ciencies Fotoniques, The Barcelona Institute of Science and Technology, 08860 Castelldefels, Spania
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 Barcelona, Spania
3Univ Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Grenoble, Frankrike
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Barcelona, Spania
Finn dette papiret interessant eller vil diskutere? Scite eller legg igjen en kommentar på SciRate.
Abstrakt
Gjensidig objektive baser tilsvarer svært nyttige målingspar i kvanteinformasjonsteori. I den minste sammensatte dimensjonen, seks, er det kjent at det eksisterer mellom tre og syv gjensidig objektive baser, med en tiår gammel formodning, kjent som Zauners formodning, som sier at det eksisterer høyst tre. Her takler vi Zauners formodning numerisk gjennom konstruksjonen av Bell-ulikheter for hvert par av heltall $n,d ge 2$ som maksimalt kan krenkes i dimensjon $d$ hvis og bare hvis $n$ MUB eksisterer i den dimensjonen. Derfor gjør vi Zauners formodning til et optimaliseringsproblem, som vi adresserer ved hjelp av tre numeriske metoder: vippeoptimalisering, ikke-lineær semidefinit programmering og Monte Carlo-teknikker. Alle tre metodene identifiserer de kjente tilfellene korrekt i lave dimensjoner, og alle antyder at det ikke eksisterer fire gjensidig objektive baser i dimensjon seks, der alle finner de samme basene som numerisk optimaliserer den tilsvarende Bell-ulikheten. Dessuten ser disse numeriske optimererne ut til å falle sammen med de "fire fjerneste basene" i dimensjon seks, funnet gjennom numerisk optimalisering av et avstandsmål i [P. Raynal, X. Lu, B.-G. Englert, {fys. Rev. A}, { 83} 062303 (2011)]. Til slutt antyder Monte Carlo-resultatene at det på det meste eksisterer tre MUB-er i dimensjon ti.
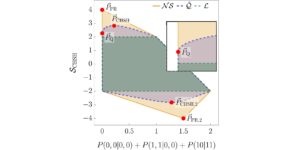
Utvalgt bilde: Den relative forskjellen mellom verdien av Bell-ulikhetene våre forutsatt at n MUB-er eksisterer i dimensjon d og verdien funnet av våre numeriske metoder. Nullverdier betyr at metodene fant n MUB i dimensjon d, mens ikke-nullverdier betyr at metodene ikke fant n MUB i dimensjon d. Alle de kjente tilfellene (dimensjoner to til fem og dimensjon seks med to og tre MUB-er) er korrekt identifisert av numerikken. I dimensjon seks finner ingen av metodene fire MUB-er, og alle metodene konvergerer til det samme settet med fire baser.
Populært sammendrag
Til tross for deres brede bruk, er det fortsatt åpne spørsmål angående strukturen til MUB-er. Mest fremtredende er det maksimale antallet målinger som er parvis objektive ("antall MUB") ukjent hvis dimensjonen til kvantesystemet er et sammensatt tall. Spesielt i dimensjon seks vet vi bare at antallet MUB-er er mellom tre og syv. En langvarig åpen formodning er den fra Zauner, som sier at det ikke eksisterer mer enn tre MUB-er i dimensjon seks. Denne tiår lange formodningen støttes av noen numeriske bevis, men det finnes ingen bevis den dag i dag.
I dette arbeidet takler vi Zauners formodning gjennom Bell ikke-lokalitet. Bell non-locality angår to eksperimentatorer som ikke har lov til å kommunisere, men som kan dele noen korrelasjoner i form av klassisk tilfeldighet eller en delt kvantetilstand. Det har vist seg at deling av kvanteressurser kan føre til eksperimentelle data som ikke kan forklares av klassisk fysikk (nærmere bestemt ved såkalte lokale skjulte variable modeller). Dette er kjent som Bells teorem, og det har blitt eksperimentelt verifisert det siste tiåret. Å være vitne til ikke-klassisiteten til eksperimentelle data gjøres oftest via såkalte Bell-ulikheter, som er funksjoner av sannsynlighetene for målingsutfall som oppstår i eksperimentet. Klassiske data må tilfredsstille Bell-ulikheter, mens kvantedata kan krenke dem.
Nylig er det funnet Bell-ulikheter som maksimalt blir brutt dersom en av partene benytter et par MUB-målinger av en gitt dimensjon. I dette arbeidet utvider vi disse ulikhetene til nye, maksimalt krenket av et utvalgt antall MUB-målinger i en gitt dimensjon. Videre, hvis dimensjonen i eksperimentet er fast, oppnås maksimal brudd hvis og bare hvis de anvendte målingene tilsvarer det valgte antallet MUB-er i den gitte dimensjonen. Derfor, å avgjøre om et utvalgt antall MUB-er eksisterer i en gitt dimensjon er ekvivalent med å finne det maksimale bruddet på den tilsvarende Bell-ulikheten i denne faste dimensjonen.
Selv om det generelt er et vanskelig problem å finne denne maksimale bruddet, bruker vi tre forskjellige numeriske metoder som et forsøk på å finne det maksimale bruddet på Bell-ulikhetene våre i en fast dimensjon. To av disse metodene er varianter av semidefinite programmeringsteknikker, mens den tredje er inspirert av statistisk fysikk og kalles simulert annealing. Selv om alle disse metodene er heuristiske - det vil si at det ikke er noen garanti for at de vil finne problemets sanne optimum - kan man måle ytelsen deres ved å bruke dem på optimaliseringsproblemer hvis optimum er kjent. Spesielt finner vi at alle de tre metodene er korrekt i stand til å identifisere MUB-målinger i de tilfellene hvor de er kjent for å eksistere. Videre, i de tilfellene hvor de er kjent for ikke å eksistere, konvergerer alle tre metodene til samme sett med målinger opp til numerisk presisjon. Vi bruker deretter metodene våre på det første ukjente tilfellet, det vil si fire MUB-er i dimensjon seks. Ingen av metodene er i stand til å identifisere fire MUB-er i dimensjon seks, men igjen konvergerer de alle til det samme settet med fire målinger opp til numerisk presisjon. Videre finner den simulerte glødeteknikken ikke fire MUB-er i neste sammensatte dimensjon, dimensjon ti. Derfor, mens strenge påstander ikke kan fremsettes på grunn av den heuristiske naturen til teknikkene våre, støtter resultatene våre Zauners formodning fra det nye perspektivet om Bells ikke-lokalitet.
► BibTeX-data
► Referanser
[1] ID Ivanovic. Geometrisk beskrivelse av kvantetilstandsbestemmelse. Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019.
https://doi.org/10.1088/0305-4470/14/12/019
[2] G. Brassard CH Bennett. Kvantekryptografi: Offentlig nøkkeldistribusjon og myntkasting. Proceedings of IEEE International Conference on Computers, Systems and Signal Processing (IEEE, 1984), 175:8, 1984. doi:10.1016/j.tcs.2011.08.039.
https: / / doi.org/ 10.1016 / j.tcs.2011.08.039
[3] Artur K. Ekert. Kvantekryptografi basert på Bells teorem. Phys. Rev. Lett., 67:661–663, 1991. doi:10.1103/PhysRevLett.67.661.
https: / / doi.org/ 10.1103 / PhysRevLett.67.661
[4] Dagmar Bruß. Optimal avlytting i kvantekryptografi med seks tilstander. Phys. Rev. Lett., 81:3018–3021, 1998. doi:10.1103/PhysRevLett.81.3018.
https: / / doi.org/ 10.1103 / PhysRevLett.81.3018
[5] Armin Tavakoli, Alley Hameedi, Breno Marques og Mohamed Bourennane. Quantum tilfeldig tilgangskoder ved hjelp av enkle $d$-nivåsystemer. Phys. Rev. Lett., 114:170502, 2015. doi:10.1103/PhysRevLett.114.170502.
https: / / doi.org/ 10.1103 / PhysRevLett.114.170502
[6] Máté Farkas og Jędrzej Kaniewski. Selvtesting av gjensidig objektive baser i forberedelse-og-mål-scenariet. Phys. Rev. A, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316.
https: / / doi.org/ 10.1103 / PhysRevA.99.032316
[7] H. Bechmann-Pasquinucci og N. Gisin. Klokkeulikhet for qunits med binære målinger. Kvanteinformasjon. Comput., 3(2):157–164, 2003. doi:10.26421/QIC3.2-6.
https: / / doi.org/ 10.26421 / QIC3.2-6
[8] Jędrzej Kaniewski, Ivan Šupić, Jordi Tura, Flavio Baccari, Alexia Salavrakos og Remigiusz Augusiak. Maksimal ikke-lokalitet fra maksimal sammenfiltring og gjensidig objektive baser, og selvtesting av kvantesystemer med to kvtrit. Quantum, 3:198, 2019. doi:10.22331/q-2019-10-24-198.
https://doi.org/10.22331/q-2019-10-24-198
[9] Armin Tavakoli, Máté Farkas, Denis Rosset, Jean-Daniel Bancal og Jędrzej Kaniewski. Gjensidig objektive baser og symmetriske informasjonsmessig komplette målinger i Bell-eksperimenter. Science Advances, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847.
https:///doi.org/10.1126/sciadv.abc3847
[10] Thomas Durt, Berthold-Georg Englert, Ingemar Bengtsson og Karol Życzkowski. På gjensidig objektive grunnlag. International Journal of Quantum Information, 08(04):535–640, 2010. doi:10.1142/S0219749910006502.
https: / / doi.org/ 10.1142 / S0219749910006502
[11] William K Wootters og Brian D Fields. Optimal tilstandsbestemmelse ved gjensidig objektive målinger. Annals of Physics, 191(2):363–381, 1989. doi:10.1016/0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
[12] Paweł Wocjan og Thomas Beth. Nykonstruksjon av gjensidig objektive baser i kvadratiske dimensjoner. Kvanteinformasjon. Comput., 5(2):93–101, 2005. doi:10.26421/QIC5.2-1.
https: / / doi.org/ 10.26421 / QIC5.2-1
[13] Mihály Weiner. Et gap for maksimalt antall gjensidig objektive baser. Proc. Amer. Matte. Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] Gerhard Zauner. Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. PhD-avhandling, 1999.
[15] P. Oscar Boykin, Meera Sitharam, Pham Huu Tiep og Pawel Wocjan. Gjensidig objektive baser og ortogonale dekomponeringer av Lie-algebraer. Kvanteinformasjon. Comput., 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https: / / doi.org/ 10.26421 / QIC7.4-6
[16] Stephen Brierley og Stefan Weigert. Konstruere gjensidig objektive baser i dimensjon seks. Phys. Rev. A, 79:052316, 2009. doi:10.1103/PhysRevA.79.052316.
https: / / doi.org/ 10.1103 / PhysRevA.79.052316
[17] Philippe Jaming, Máté Matolcsi, Péter Móra, Ferenc Szöllősi og Mihály Weiner. Et generalisert Pauli-problem og en uendelig familie av MUB-tripletter i dimensjon 6. Journal of Physics A: Mathematical and Theoretical, 42(24):245305, mai 2009. doi:10.1088/1751-8113/42/24/ 245305.
https://doi.org/10.1088/1751-8113/42/24/245305
[18] Gary McConnell, Harry Spencer og Afaq Tahir. Bevis for og mot Zauners MUB-formodning i $mathbb{C}^6$. 2021. doi:10.48550/arXiv.2103.08703.
https:///doi.org/10.48550/arXiv.2103.08703
[19] Sander Gribling og Sven Polak. Gjensidig objektive baser: polynomoptimalisering og symmetri. 2021. doi:10.48550/arXiv.2111.05698.
https:///doi.org/10.48550/arXiv.2111.05698
[20] Ingemar Bengtsson, Wojciech Bruzda, Åsa Ericsson, Jan-Åke Larsson, Wojciech Tadej og Karol Życzkowski. Gjensidig objektive baser og Hadamard-matriser av størrelsesorden seks. Journal of Mathematical Physics, 48(5):052106, 2007. doi:10.1063/1.2716990.
https: / / doi.org/ 10.1063 / 1.2716990
[21] Philippe Raynal, Xin Lü og Berthold-Georg Englert. Gjensidig objektive baser i seks dimensjoner: De fire mest fjerne baser. Phys. Rev. A, 83:062303, 2011. doi:10.1103/PhysRevA.83.062303.
https: / / doi.org/ 10.1103 / PhysRevA.83.062303
[22] Edgar A. Aguilar, Jakub J. Borkała, Piotr Mironowicz og Marcin Pawłowski. Forbindelser mellom gjensidig objektive baser og kvantetilfeldige tilgangskoder. Phys. Rev. Lett., 121:050501, 2018. doi:10.1103/PhysRevLett.121.050501.
https: / / doi.org/ 10.1103 / PhysRevLett.121.050501
[23] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani og Stephanie Wehner. Bell ikke-lokalitet. Rev. Mod. Phys., 86:419–478, 2014. doi:10.1103/RevModPhys.86.419.
https: / / doi.org/ 10.1103 / RevModPhys.86.419
[24] MOSEK ApS. MOSEK Fusion API for C++ 9.2.49, 2021. URL: https:///docs.mosek.com/9.2/cxxfusion/index.html.
https:///docs.mosek.com/9.2/cxxfusion/index.html
[25] Hiroshi Yamashita, Hiroshi Yabe og Kouhei Harada. En primal-dobbelt indre punktmetode for ikke-lineær semibestemt programmering. Matematisk programmering, 135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z.
https: / / doi.org/ 10.1007 / s10107-011-0449-z
[26] Stephen Boyd og Lieven Vandenberghe. Konveks optimalisering. Cambridge University Press, 2004. doi: 10.1017 / CBO9780511804441.
https: / / doi.org/ 10.1017 / CBO9780511804441
[27] S. Kirkpatrick, CD Gelatt og MP Vecchi. Optimalisering ved simulert gløding. Science, 220(4598):671–680, 1983. doi:10.1126/science.220.4598.671.
https: / / doi.org/ 10.1126 / science.220.4598.671
[28] Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller og Edward Teller. Ligning av tilstandsberegninger ved hjelp av raske datamaskiner. The Journal of Chemical Physics, 21(6):1087–1092, 1953. doi:10.1063/1.1699114.
https: / / doi.org/ 10.1063 / 1.1699114
[29] Miguel Navascués, Stefano Pironio og Antonio Acín. Avgrense settet med kvantekorrelasjoner. Phys. Rev. Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401.
https: / / doi.org/ 10.1103 / PhysRevLett.98.010401
Sitert av
Denne artikkelen er utgitt i Quantum under Creative Commons Attribution 4.0 International (CC BY 4.0) tillatelse. Opphavsrett forblir hos de opprinnelige rettighetshaverne som forfatterne eller institusjonene deres.