Classification Of Measurement-based Quantum Wire In Stabilizer PEPS

Republished By Plato

Followers: 0

Paul Herringer and Robert Raussendorf

Department of Physics and Astronomy, University of British Columbia, Vancouver, Canada
Stewart Blusson Quantum Matter Institute, University of British Columbia, Vancouver, Canada

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

We consider a class of translation-invariant 2D tensor network states with a stabilizer symmetry, which we call stabilizer PEPS. The cluster state, GHZ state, and states in the toric code belong to this class. We investigate the transmission capacity of stabilizer PEPS for measurement-based quantum wire, and arrive at a complete classification of transmission behaviors. The transmission behaviors fall into 13 classes, one of which corresponds to Clifford quantum cellular automata. In addition, we identify 12 other classes.

Classification of measurement-based quantum wire in stabilizer PEPS PlatoBlockchain Data Intelligence. Vertical Search. Ai.

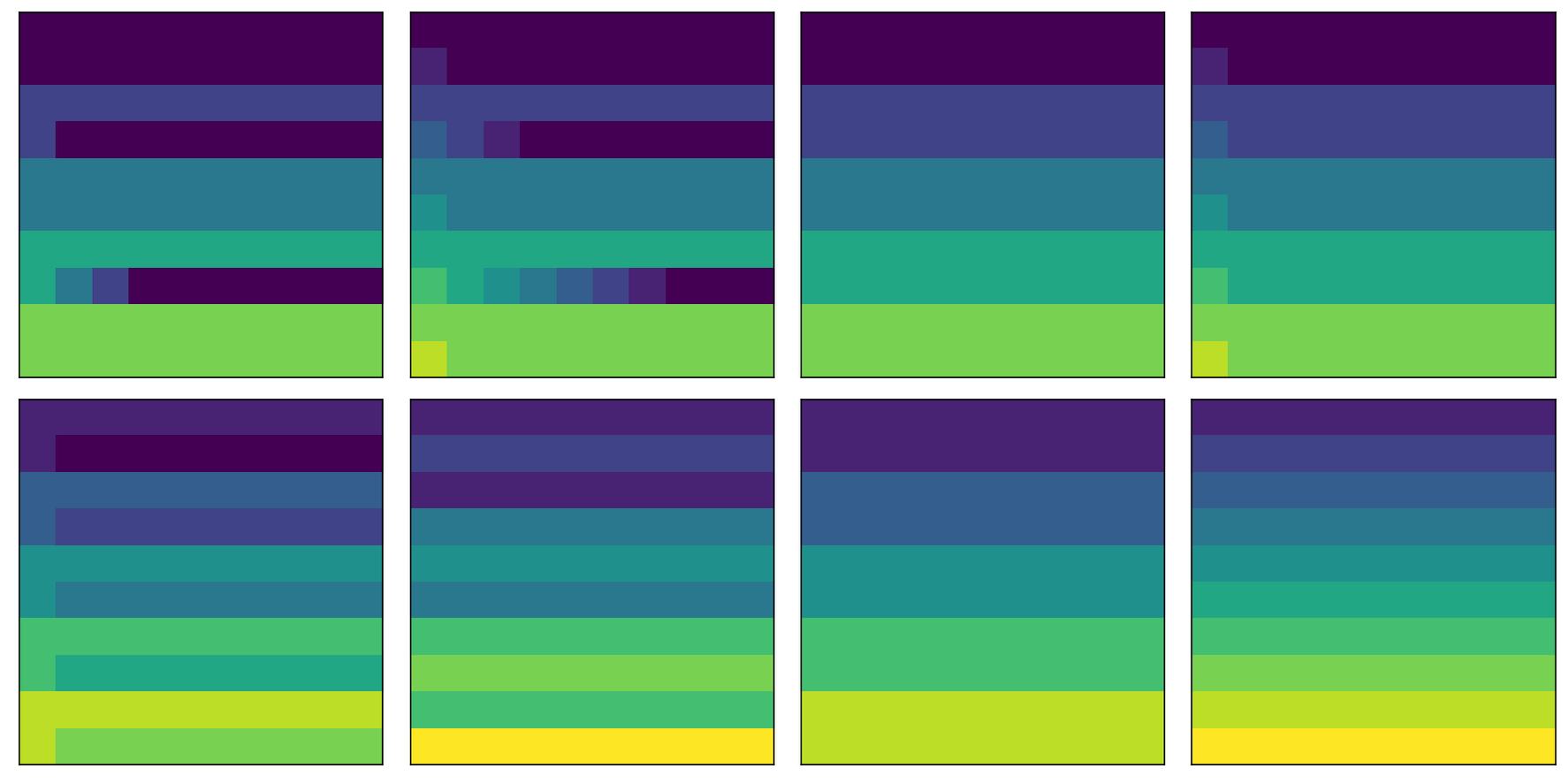
Featured image: Transmission capacity for measurement-based quantum wire as a function of the circumference (vertical axis) and depth (horizontal axis) of a cylindrical stabilizer PEPS falls into one of 13 classes. Shown here are characteristic plots for 8 of these classes, including the class of Clifford quantum cellular automata (bottom right).

Popular summary

Symmetry is ubiquitous in nature, and it helps us simplify and classify phenomena of the physical world. In this paper, we leverage symmetry to classify a family of many-body quantum states by their entanglement structure. With the help of single-particle measurements, entanglement can be harnessed to transmit quantum information in a process known as measurement-based quantum wire. Consequently, our findings establish a classification of quantum states based on their suitability for measurement-based quantum wire. In doing so, we lay the groundwork for a future classification of quantum states and phases by their usefulness for universal measurement-based quantum computation.

► BibTeX data

@article{Herringer2023classificationof, doi = {10.22331/q-2023-06-12-1041}, url = {https://doi.org/10.22331/q-2023-06-12-1041}, title = {Classification of measurement-based quantum wire in stabilizer {PEPS}}, author = {Herringer, Paul and Raussendorf, Robert}, journal = {{Quantum}}, issn = {2521-327X}, publisher = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, volume = {7}, pages = {1041}, month = jun, year = {2023}<br /> }

► References

[1] E. Schrödinger. “Probability relations between separated systems”. Mathematical Proceedings of the Cambridge Philosophical Society 32, 446–452 (1936).
https://doi.org/10.1017/S0305004100019137

[2] H. M. Wiseman, S. J. Jones, and A. C. Doherty. “Steering, Entanglement, Nonlocality, and the Einstein-Podolsky-Rosen Paradox”. Physical Review Letters 98, 140402 (2007).
https://doi.org/10.1103/PhysRevLett.98.140402

[3] M. Popp, F. Verstraete, M. A. Martín-Delgado, and J. I. Cirac. “Localizable entanglement”. Physical Review A 71, 042306 (2005).
https://doi.org/10.1103/PhysRevA.71.042306

[4] Charles H. Bennett, Gilles Brassard, Sandu Popescu, Benjamin Schumacher, John A. Smolin, and William K. Wootters. “Purification of Noisy Entanglement and Faithful Teleportation via Noisy Channels”. Physical Review Letters 76, 722–725 (1996).
https://doi.org/10.1103/PhysRevLett.76.722

[5] H.-J. Briegel, W. Dür, J. I. Cirac, and P. Zoller. “Quantum Repeaters: The Role of Imperfect Local Operations in Quantum Communication”. Physical Review Letters 81, 5932–5935 (1998).
https://doi.org/10.1103/PhysRevLett.81.5932

[6] Robert Raussendorf and Hans J Briegel. “A One-Way Quantum Computer”. Physical Review Letters 86, 5188–5191 (2001).
https://doi.org/10.1103/PhysRevLett.86.5188

[7] Hans J. Briegel and Robert Raussendorf. “Persistent Entanglement in Arrays of Interacting Particles”. Physical Review Letters 86, 910–913 (2001).
https://doi.org/10.1103/PhysRevLett.86.910

[8] Dominic V. Else, Ilai Schwarz, Stephen D. Bartlett, and Andrew C. Doherty. “Symmetry-Protected Phases for Measurement-Based Quantum Computation”. Physical Review Letters 108, 240505 (2012).
https://doi.org/10.1103/PhysRevLett.108.240505

[9] Tzu-Chieh Wei, Ian Affleck, and Robert Raussendorf. “Affleck-Kennedy-Lieb-Tasaki State on a Honeycomb Lattice is a Universal Quantum Computational Resource”. Physical Review Letters 106, 070501 (2011).
https://doi.org/10.1103/PhysRevLett.106.070501

[10] Akimasa Miyake. “Quantum computational capability of a 2D valence bond solid phase”. Annals of Physics 326, 1656–1671 (2011).
https://doi.org/10.1016/j.aop.2011.03.006

[11] Akimasa Miyake. “Quantum Computation on the Edge of a Symmetry-Protected Topological Order”. Physical Review Letters 105, 040501 (2010).
https://doi.org/10.1103/PhysRevLett.105.040501

[12] Jacob Miller and Akimasa Miyake. “Resource Quality of a Symmetry-Protected Topologically Ordered Phase for Quantum Computation”. Physical Review Letters 114, 120506 (2015).
https://doi.org/10.1103/PhysRevLett.114.120506

[13] Robert Raussendorf, Dong-Sheng Wang, Abhishodh Prakash, Tzu-Chieh Wei, and David T. Stephen. “Symmetry-protected topological phases with uniform computational power in one dimension”. Physical Review A 96, 012302 (2017).
https://doi.org/10.1103/PhysRevA.96.012302

[14] Trithep Devakul and Dominic J. Williamson. “Universal quantum computation using fractal symmetry-protected cluster phases”. Physical Review A 98, 022332 (2018).
https://doi.org/10.1103/PhysRevA.98.022332

[15] Austin K. Daniel, Rafael N. Alexander, and Akimasa Miyake. “Computational universality of symmetry-protected topologically ordered cluster phases on 2D Archimedean lattices”. Quantum 4, 228 (2020).
https://doi.org/10.22331/q-2020-02-10-228

[16] Austin K. Daniel and Akimasa Miyake. “Quantum Computational Advantage with String Order Parameters of One-Dimensional Symmetry-Protected Topological Order”. Physical Review Letters 126, 090505 (2021).
https://doi.org/10.1103/PhysRevLett.126.090505

[17] Robert Raussendorf, Cihan Okay, Dong-Sheng Wang, David T. Stephen, and Hendrik Poulsen Nautrup. “Computationally Universal Phase of Quantum Matter”. Physical Review Letters 122, 090501 (2019).
https://doi.org/10.1103/PhysRevLett.122.090501

[18] David T. Stephen, Hendrik Poulsen Nautrup, Juani Bermejo-Vega, Jens Eisert, and Robert Raussendorf. “Subsystem symmetries, quantum cellular automata, and computational phases of quantum matter”. Quantum 3, 142 (2019).
https://doi.org/10.22331/q-2019-05-20-142

[19] Tzu-Chieh Wei and Robert Raussendorf. “Universal measurement-based quantum computation with spin-2 Affleck-Kennedy-Lieb-Tasaki states”. Physical Review A 92, 012310 (2015).
https://doi.org/10.1103/PhysRevA.92.012310

[20] Dirk-M. Schlingemann, Holger Vogts, and Reinhard F. Werner. “On the structure of Clifford quantum cellular automata”. Journal of Mathematical Physics 49, 112104 (2008).
https://doi.org/10.1063/1.3005565

[21] A.Yu Kitaev. “Fault-tolerant quantum computation by anyons”. Annals of Physics 303, 2–30 (2003).
https://doi.org/10.1016/S0003-4916(02)00018-0

[22] B. Schumacher and R. F. Werner. “Reversible quantum cellular automata” (2004). arXiv:quant-ph/0405174.
arXiv:quant-ph/0405174

[23] Daniel M Greenberger, Michael A Horne, and Anton Zeilinger. “Going Beyond Bell’s Theorem”. In Menas Kafatos, editor, Bell’s Theorem, Quantum Theory and Conceptions of the Universe. Pages 69–72. Springer Netherlands, Dordrecht (1989).
https://doi.org/10.1007/978-94-017-0849-4_10

[24] Daniel M. Greenberger, Michael A. Horne, Abner Shimony, and Anton Zeilinger. “Bell’s theorem without inequalities”. American Journal of Physics 58, 1131–1143 (1990).
https://doi.org/10.1119/1.16243

[25] W. Dür, G. Vidal, and J. I. Cirac. “Three qubits can be entangled in two inequivalent ways”. Physical Review A 62, 062314 (2000).
https://doi.org/10.1103/PhysRevA.62.062314

[26] M. Sanz, I. L. Egusquiza, R. Di Candia, H. Saberi, L. Lamata, and E. Solano. “Entanglement classification with matrix product states”. Scientific Reports 6, 30188 (2016).
https://doi.org/10.1038/srep30188

[27] Norbert Schuch, David Pérez-García, and Ignacio Cirac. “Classifying quantum phases using matrix product states and projected entangled pair states”. Physical Review B 84, 165139 (2011).
https://doi.org/10.1103/PhysRevB.84.165139

[28] R. Raussendorf, J. Harrington, and K. Goyal. “Topological fault-tolerance in cluster state quantum computation”. New Journal of Physics 9, 199–199 (2007).
https://doi.org/10.1088/1367-2630/9/6/199

[29] Sergey Bravyi and Robert Raussendorf. “Measurement-based quantum computation with the toric code states”. Physical Review A 76, 022304 (2007).
https://doi.org/10.1103/PhysRevA.76.022304

[30] Sergey Bravyi, David Gosset, and Yinchen Liu. “How to Simulate Quantum Measurement without Computing Marginals”. Physical Review Letters 128, 220503 (2022).
https://doi.org/10.1103/PhysRevLett.128.220503

[31] Xiao-Gang Wen. “Quantum orders in an exact soluble model”. Physical Review Letters 90, 016803 (2003).
https://doi.org/10.1103/PhysRevLett.90.016803

[32] Alastair Kay. “The Capabilities of a Perturbed Toric Code as a Quantum Memory”. Physical Review Letters 107, 270502 (2011).
https://doi.org/10.1103/PhysRevLett.107.270502

[33] Lorenzo Piroli, Georgios Styliaris, and J. Ignacio Cirac. “Quantum Circuits Assisted by Local Operations and Classical Communication: Transformations and Phases of Matter”. Physical Review Letters 127, 220503 (2021).
https://doi.org/10.1103/PhysRevLett.127.220503

[34] https://doi.org/10.5281/zenodo.7742735.
https://doi.org/10.5281/zenodo.7742735

[35] David Fattal, Toby S. Cubitt, Yoshihisa Yamamoto, Sergey Bravyi, and Isaac L. Chuang. “Entanglement in the stabilizer formalism” (2004). arXiv:quant-ph/0406168.
arXiv:quant-ph/0406168

Cited by

[1] David T. Stephen, Wen Wei Ho, Tzu-Chieh Wei, Robert Raussendorf, and Ruben Verresen, “Universal measurement-based quantum computation in a one-dimensional architecture enabled by dual-unitary circuits”, arXiv:2209.06191, (2022).

[2] Michael de Oliveira, Luís S. Barbosa, and Ernesto F. Galvão, “Quantum advantage in temporally flat measurement-based quantum computation”, arXiv:2212.03668, (2022).

The above citations are from SAO/NASA ADS (last updated successfully 2023-06-12 23:53:38). The list may be incomplete as not all publishers provide suitable and complete citation data.

On Crossref’s cited-by service no data on citing works was found (last attempt 2023-06-12 23:53:37).

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.