“Proper” Shift Rules for Derivatives of Perturbed-Parametric Quantum Evolutions

“Proper” Shift Rules for Derivatives of Perturbed-Parametric Quantum Evolutions

Time Stamp: July 11, 2023 5:48 AM

Dirk Oliver Theis

Theoretical Computer Science, University of Tartu, Estonia

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

Banchi & Crooks (Quantum, 2021) have given methods to estimate derivatives of expectation values depending on a parameter that enters via what we call a “perturbed” quantum evolution $xmapsto e^{i(x A + B)/hbar}$. Their methods require modifications, beyond merely changing parameters, to the unitaries that appear. Moreover, in the case when the $B$-term is unavoidable, no exact method (unbiased estimator) for the derivative seems to be known: Banchi & Crooks’s method gives an approximation.
In this paper, for estimating the derivatives of parameterized expectation values of this type, we present a method that only requires shifting parameters, no other modifications of the quantum evolutions (a “proper” shift rule). Our method is exact (i.e., it gives analytic derivatives, unbiased estimators), and it has the same worst-case variance as Banchi-Crooks’s.
Moreover, we discuss the theory surrounding proper shift rules, based on Fourier analysis of perturbed-parametric quantum evolutions, resulting in a characterization of the proper shift rules in terms of their Fourier transforms, which in turn leads us to non-existence results of proper shift rules with exponential concentration of the shifts. We derive truncated methods that exhibit approximation errors, and compare to Banchi-Crooks’s based on preliminary numerical simulations.

“Proper” Shift Rules for Derivatives of Perturbed-Parametric Quantum Evolutions PlatoBlockchain Data Intelligence. Vertical Search. Ai.

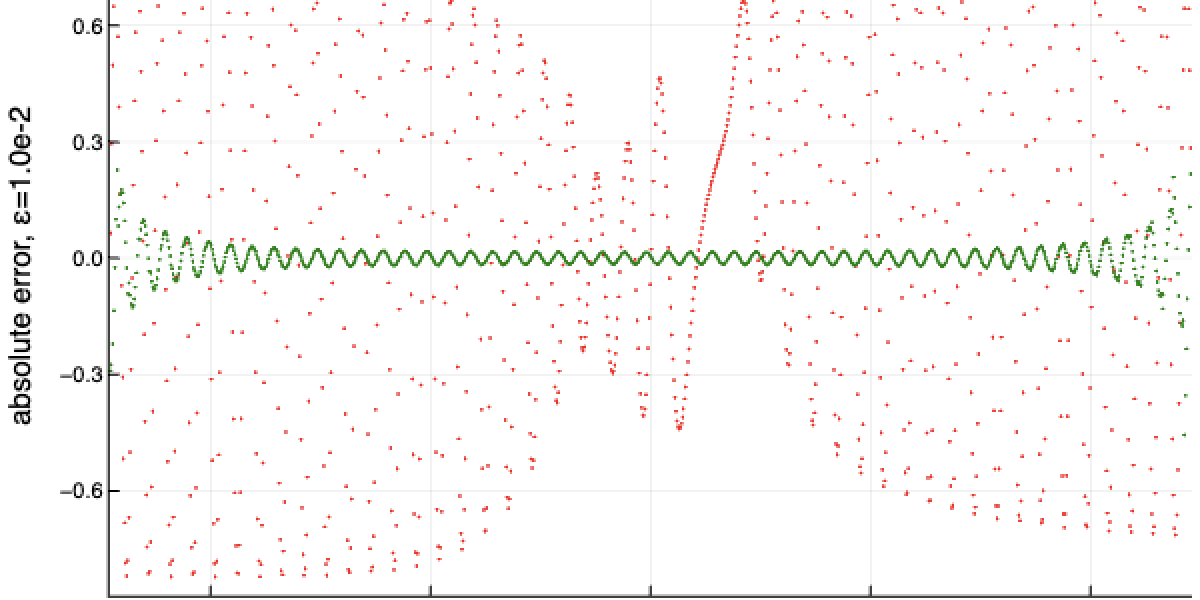
Featured image: Preliminary numerical results indicate that the new method is better than the state-of-the art. Here is a plot showing, for one randomly chosen parameterized quantum evolution, the error (bias) in estimating the derivatives on the vertical, and the parameter value on the horizontal. The green dots show the error of the new method, the red dots give the state of the art. (Other performance variables are fixed and equal for both methods.)

Popular summary

In attempts to use current-day or near-future quantum devices for meaningful computations, the variational hybrid quantum-classical approach is widely pursued. It consists in parameterizing the quantum evolution and then optimizing these parameters in a loop, alternating between quantum and classical computation.

Another approach consists in mapping a computational problem to a Hamiltonian that can be realized on quantum hardware. For example, for modeling the Maximum Stable Set problem on cold-atom quantum devices, the Rydberg blockade may serve as a way to partially realize the stability constraints.

Attempts are, of course, under way to combine the two approaches.

For optimizing the parameters, the variational approach typically employs estimators of the gradient, and these estimators should have small bias and small variance. In the digital quantum computing world — i.e., quantum circuits containing (parameterized) gates gates — estimating the gradients is well understood, and based on so-called 𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟 𝑠ℎ𝑖𝑓𝑡 𝑟𝑢𝑙𝑒𝑠. But when combining the digital with the analog, the situation arises that the parameterized part of the Hamiltonian does not commute with other parts.
Think of choosing as one of the parameters the Rabi frequency, say locally to a single atom, in an array of Rydberg atoms: The Rabi term does not commute with the Rydberg blockade terms. Many more examples exist. In these situations, the known shift-rule theory breaks down.
In our paper, we propose a new method for estimating derivatives for these situations. Our method works along the known shift-rule paradigm, and improves upon the state of the art in reducing the bias of the estimator.

► BibTeX data

► References

[1] Jarrod R McClean, Nicholas C Rubin, Joonho Lee, Matthew P Harrigan, Thomas E O’Brien, Ryan Babbush, William J Huggins, and Hsin-Yuan Huang. “What the foundations of quantum computer science teach us about chemistry”. The Journal of Chemical Physics 155, 150901 (2021).
https:/​/​doi.org/​10.48550/​arXiv.2106.03997

[2] Xiao Yuan, Suguru Endo, Qi Zhao, Ying Li, and Simon C Benjamin. “Theory of variational quantum simulation”. Quantum 3, 191 (2019).
https:/​/​doi.org/​10.48550/​arXiv.1812.08767

[3] Kosuke Mitarai, Makoto Negoro, Masahiro Kitagawa, and Keisuke Fujii. “Quantum circuit learning”. Phys. Rev. A 98, 032309 (2018).
https:/​/​doi.org/​10.1103/​PhysRevA.98.032309

[4] Marcello Benedetti, Erika Lloyd, Stefan Sack, and Mattia Fiorentini. “Parameterized quantum circuits as machine learning models”. Quantum Science and Technology 4, 043001 (2019).
https:/​/​doi.org/​10.1088/​2058-9565/​ab4eb5

[5] Edward Farhi, Jeffrey Goldstone, and Sam Gutmann. “A quantum approximate optimization algorithm”. Preprint (2014).
https:/​/​doi.org/​10.48550/​arXiv.1411.4028

[6] Eric R Anschuetz, Jonathan P Olson, Alán Aspuru-Guzik, and Yudong Cao. “Variational quantum factoring”. Preprint (2018).
https:/​/​doi.org/​10.48550/​arXiv.1808.08927

[7] Carlos Bravo-Prieto, Ryan LaRose, Marco Cerezo, Yigit Subasi, Lukasz Cincio, and Patrick J Coles. “Variational quantum linear solver”. Preprint (2019).
https:/​/​doi.org/​10.48550/​arXiv.1909.05820

[8] Ryan Babbush and Hartmut Neven. “Training quantum evolutions using sublogical controls” (2019). US Patent 10,275,717.

[9] Louis-Paul Henry, Slimane Thabet, Constantin Dalyac, and Loïc Henriet. “Quantum evolution kernel: Machine learning on graphs with programmable arrays of qubits”. Physical Review A 104, 032416 (2021).
https:/​/​doi.org/​10.48550/​arXiv.2107.03247

[10] Constantin Dalyac, Loïc Henriet, Emmanuel Jeandel, Wolfgang Lechner, Simon Perdrix, Marc Porcheron, and Margarita Veshchezerova. “Qualifying quantum approaches for hard industrial optimization problems. a case study in the field of smart-charging of electric vehicles”. EPJ Quantum Technology 8, 12 (2021).
https:/​/​doi.org/​10.48550/​arXiv.2012.14859

[11] Ryan Sweke, Frederik Wilde, Johannes Meyer, Maria Schuld, Paul K Fährmann, Barthélémy Meynard-Piganeau, and Jens Eisert. “Stochastic gradient descent for hybrid quantum-classical optimization”. Quantum 4, 314 (2020).
https:/​/​doi.org/​10.48550/​arXiv.1910.01155

[12] Jun Li, Xiaodong Yang, Xinhua Peng, and Chang-Pu Sun. “Hybrid quantum-classical approach to quantum optimal control”. Phys. Rev. Lett. 118, 150503 (2017).
https:/​/​doi.org/​10.1103/​PhysRevLett.118.150503

[13] Leonardo Banchi and Gavin E. Crooks. “Measuring analytic gradients of general quantum evolution with the stochastic parameter shift rule”. Quantum 5, 386 (2021).
https:/​/​doi.org/​10.22331/​q-2021-01-25-386

[14] Richard P Feynman. “An operator calculus having applications in quantum electrodynamics”. Physical Review 84, 108 (1951).
https:/​/​doi.org/​10.1103/​PhysRev.84.108

[15] Ralph M Wilcox. “Exponential operators and parameter differentiation in quantum physics”. Journal of Mathematical Physics 8, 962–982 (1967).
https:/​/​doi.org/​10.1063/​1.1705306

[16] Javier Gil Vidal and Dirk Oliver Theis. “Calculus on parameterized quantum circuits”. Preprint (2018).
https:/​/​doi.org/​10.48550/​arXiv.1812.06323

[17] David Wierichs, Josh Izaac, Cody Wang, and Cedric Yen-Yu Lin. “General parameter-shift rules for quantum gradients”. Preprint (2021).
https:/​/​doi.org/​10.48550/​arXiv.2107.12390

[18] Dirk Oliver Theis. “Optimality of finite-support parameter shift rules for derivatives of variational quantum circuits”. Preprint (2021).
https:/​/​doi.org/​10.48550/​arXiv.2112.14669

[19] Michael Reed and Barry Simon. “Methods of Modern Mathematical Physics II: Fourier Analysis, Self-Adjointness”. Volume 2. Academic Press. (1975).

[20] Jarrod R McClean, Sergio Boixo, Vadim N Smelyanskiy, Ryan Babbush, and Hartmut Neven. “Barren plateaus in quantum neural network training landscapes”. Nature communications 9, 4812 (2018).
https:/​/​doi.org/​10.1038/​s41467-018-07090-4

[21] Andrew Arrasmith, Zoë Holmes, Marco Cerezo, and Patrick J Coles. “Equivalence of quantum barren plateaus to cost concentration and narrow gorges”. Quantum Science and Technology 7, 045015 (2022).
https:/​/​doi.org/​10.48550/​arXiv.2104.05868

[22] Walter Rudin. “Functional Analysis”. McGraw-Hill. (1991).

[23] Elias M Stein and Rami Shakarchi. “Fourier Analysis: An Introduction”. Volume 1. Princeton University Press. (2011).

[24] Gerald B Folland. “A Course in Abstract Harmonic Analysis”. Volume 29. CRC press. (2016).

[25] Don Zagier. “The dilogarithm function”. In Frontiers in number theory, physics, and geometry II. Pages 3–65. Springer (2007).

[26] Leonard C Maximon. “The dilogarithm function for complex argument”. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 459, 2807–2819 (2003).
https:/​/​doi.org/​10.1098/​rspa.2003.1156

[27] Elias M Stein and Rami Shakarchi. “Complex Analysis”. Volume 2. Princeton University Press. (2010).

[28] Walter Rudin. “Real and Complex Analysis”. McGraw-Hill. (1987).

[29] Heinz Bauer. “Maß- und Integrationstheorie”. Walter de Gruyter. (1992). 2nd edition.

[30] Franz Rellich and Joseph Berkowitz. “Perturbation Theory of Eigenvalue Problems”. CRC Press. (1969).

Cited by

[1] Roeland Wiersema, Dylan Lewis, David Wierichs, Juan Carrasquilla, and Nathan Killoran, “Here comes the $mathrm{SU}(N)$: multivariate quantum gates and gradients”, arXiv:2303.11355, (2023).

The above citations are from SAO/NASA ADS (last updated successfully 2023-07-14 10:03:06). The list may be incomplete as not all publishers provide suitable and complete citation data.

On Crossref’s cited-by service no data on citing works was found (last attempt 2023-07-14 10:03:04).

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.

Time Stamp:

More from Quantum Journal