Nova prova aponta a agulha para um problema de geometria pegajosa | Revista Quanta

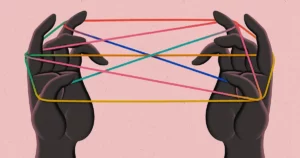
Em 1917, o matemático japonês Sōichi Kakeya propôs o que a princípio parecia nada mais do que um divertido exercício de geometria. Coloque uma agulha infinitamente fina, com uma polegada de comprimento, em uma superfície plana e gire-a para que ela aponte em todas as direções. Qual é a menor área que a agulha pode varrer?

Se você simplesmente girá-lo em torno de seu centro, obterá um círculo. Mas é possível mover a agulha de maneiras criativas, de modo que você esculpe uma quantidade muito menor de espaço. Desde então, os matemáticos apresentaram uma versão relacionada a essa questão, chamada de conjectura de Kakeya. Em suas tentativas de resolvê-lo, eles descobriram conexões surpreendentes com a análise harmônica, a teoria dos números e até a física.

“De alguma forma, essa geometria de linhas apontando em muitas direções diferentes é onipresente em grande parte da matemática”, disse jonathan hickman da Universidade de Edimburgo.

Mas também é algo que os matemáticos ainda não entendem completamente. Nos últimos anos, eles provaram variações da conjectura de Kakeya em configurações mais fáceis, mas a questão permanece sem solução no espaço tridimensional normal. Por algum tempo, parecia que todo o progresso havia parado nessa versão da conjectura, embora ela tenha inúmeras consequências matemáticas.

Agora, dois matemáticos moveram a agulha, por assim dizer. Sua nova prova derruba um grande obstáculo isso existe há décadas - reacendendo a esperança de que uma solução possa finalmente estar à vista.

Qual é o Pequeno Negócio?

Kakeya estava interessado em conjuntos no plano que contêm um segmento de linha de comprimento 1 em todas as direções. Existem muitos exemplos desses conjuntos, sendo o mais simples um disco com um diâmetro de 1. Kakeya queria saber como seria o menor desses conjuntos.

Ele propôs um triângulo com lados ligeiramente côncavos, chamado deltóide, que tem metade da área do disco. Descobriu-se, no entanto, que é possível fazer muito, muito melhor.

Em 1919, apenas alguns anos depois que Kakeya apresentou seu problema, o matemático russo Abram Besicovitch mostrou que, se você organizar suas agulhas de uma maneira muito particular, poderá construir um conjunto de aparência espinhosa com uma área arbitrariamente pequena. (Devido à Primeira Guerra Mundial e à Revolução Russa, seu resultado não chegaria ao resto do mundo matemático por vários anos.)

Para ver como isso pode funcionar, pegue um triângulo e divida-o ao longo de sua base em pedaços triangulares mais finos. Em seguida, deslize essas peças para que se sobreponham o máximo possível, mas se projetem em direções ligeiramente diferentes. Repetindo o processo várias vezes - subdividindo seu triângulo em fragmentos cada vez mais finos e reorganizando-os cuidadosamente no espaço - você pode tornar seu conjunto tão pequeno quanto desejar. No limite infinito, você pode obter um conjunto que matematicamente não tem área, mas ainda pode, paradoxalmente, acomodar uma agulha apontando em qualquer direção.

“Isso é meio surpreendente e contra-intuitivo”, disse Rui Xiang Zhang da Universidade da Califórnia, Berkeley. “É um conjunto muito patológico.”

Esse resultado pode ser generalizado para dimensões maiores: é possível construir um conjunto com volume arbitrariamente pequeno que contenha um segmento de linha unitário apontando em todas as direções em nespaço tridimensional.

Besicovitch parecia ter resolvido completamente a questão de Kakeya. Mas décadas depois, os matemáticos começaram a trabalhar em outra versão do problema em que substituíram a área (ou volume, no caso de dimensão superior) por uma noção diferente de tamanho.

Para entender essa reformulação da questão, primeiro pegue cada segmento de linha em um conjunto Kakeya e aumente um pouco - como se você estivesse usando uma agulha real, em vez de uma agulha idealizada. No plano, seu conjunto consistirá em retângulos extremamente finos; no espaço tridimensional, você terá uma coleção de tubos extremamente finos.

Esses conjuntos gordos sempre têm alguma área (ou volume, mas vamos nos ater ao caso bidimensional por enquanto). À medida que você altera a largura da agulha, essa área também muda. Na década de 1970, o matemático Roy Davies (que morreu no mês passado) mostrou que, se a área total mudar um pouco, a largura de cada agulha deve mudar drasticamente. Por exemplo, se você deseja que uma versão engordada do conjunto de Besicovitch tenha uma área de 1/10 de polegada quadrada, cada agulha precisa ter uma espessura de cerca de 0.000045 polegada: e^-10 de uma polegada, para ser preciso. Mas se você quisesse fazer a área total 1/100 de polegada quadrada - 10 vezes menor - a agulha teria que ser e^-100 de uma polegada de espessura. (Quarenta e três zeros seguem o ponto decimal antes de chegar aos outros dígitos.)

“Se você me disser o quão pequena você quer que a área seja, então eu tenho que exigir uma agulha que seja incrivelmente fina”, disse Carlos Fefferman da Universidade de Princeton.

Os matemáticos medem o “tamanho” do conjunto Kakeya usando uma quantidade chamada dimensão de Minkowski, que está relacionada, mas não exatamente igual, a uma dimensão comum (definida como o número de direções independentes necessárias para descrever um espaço).

Aqui está uma maneira de pensar sobre a dimensão de Minkowski: pegue seu conjunto e cubra-o com pequenas bolas, cada uma com um diâmetro de um milionésimo de sua unidade preferida. Se o seu conjunto for um segmento de linha de comprimento 1, você precisará de pelo menos 1 milhão de bolas para cobri-lo. Se o seu conjunto for um quadrado de área 1, você precisará de muitos, muitos mais: um milhão ao quadrado ou um trilhão. Para uma esfera de volume 1, é cerca de 1 milhão ao cubo (um quintilhão) e assim por diante. A dimensão de Minkowski é o valor desse expoente. Ele mede a taxa na qual o número de bolas que você precisa para cobrir seu conjunto cresce à medida que o diâmetro de cada bola diminui. Um segmento de reta tem dimensão 1, um quadrado tem dimensão 2 e um cubo tem dimensão 3.

Essas dimensões são familiares. Mas usando a definição de Minkowski, torna-se possível construir um conjunto que tenha uma dimensão de, digamos, 2.7. Embora tal conjunto não preencha o espaço tridimensional, é em certo sentido “maior” do que uma superfície bidimensional.

Quando você cobre um conjunto com bolas de um determinado diâmetro, está aproximando o volume da versão engordada do conjunto. Quanto mais lentamente o volume do conjunto diminuir com o tamanho da sua agulha, mais bolas você precisará para cobri-lo. Portanto, você pode reescrever o resultado de Davies — que afirma que a área de um conjunto Kakeya no plano diminui lentamente — para mostrar que o conjunto deve ter uma dimensão de Minkowski igual a 2. A conjectura de Kakeya generaliza essa afirmação para dimensões superiores: Um conjunto Kakeya deve tem sempre a mesma dimensão do espaço que habita.

Essa simples afirmação tem sido surpreendentemente difícil de provar.

Uma Torre de Conjecturas

Até que Fefferman fez uma descoberta surpreendente em 1971, a conjectura foi vista como uma curiosidade.

Ele estava trabalhando em um problema totalmente diferente na época. Ele queria entender a transformada de Fourier, uma ferramenta poderosa que permite aos matemáticos estudar funções escrevendo-as como somas de ondas senoidais. Pense em uma nota musical, que é composta de muitas frequências sobrepostas. (É por isso que um dó central em um piano soa diferente de um dó central em um violino.) A transformada de Fourier permite que os matemáticos calculem as frequências constituintes de uma determinada nota. O mesmo princípio funciona para sons tão complicados quanto a fala humana.

Os matemáticos também querem saber se podem reconstruir a função original se receberem apenas algumas de suas infinitas frequências constituintes. Eles têm um bom entendimento de como fazer isso em uma dimensão. Mas em dimensões superiores, eles podem fazer escolhas diferentes sobre quais frequências usar e quais ignorar. Fefferman provou, para surpresa de seus colegas, que você pode falhar em reconstruir sua função ao confiar em uma maneira particularmente conhecida de escolher frequências.

Sua prova dependia da construção de uma função modificando o conjunto Kakeya de Besicovitch. Mais tarde, isso inspirou os matemáticos a desenvolver uma hierarquia de conjecturas sobre o comportamento de dimensão superior da transformada de Fourier. Hoje, a hierarquia inclui até conjecturas sobre o comportamento de importantes equações diferenciais parciais da física, como a equação de Schrödinger. Cada conjectura na hierarquia implica automaticamente aquela abaixo dela.

A conjectura Kakeya está bem na base desta torre. Se for falso, então as declarações superiores na hierarquia também são. Por outro lado, provar que é verdadeiro não implicaria imediatamente na verdade das conjecturas localizadas acima dele, mas poderia fornecer ferramentas e insights para atacá-las.

“O incrível sobre a conjectura de Kakeya é que não é apenas um problema divertido; é um verdadeiro gargalo teórico”, disse Hickman. “Não entendemos muitos desses fenômenos nas equações diferenciais parciais e na análise de Fourier porque não entendemos esses conjuntos de Kakeya.”

Incubando um plano

A prova de Fefferman — juntamente com as conexões posteriormente descobertas com a teoria dos números, combinatória e outras áreas — reavivou o interesse no problema de Kakeya entre os principais matemáticos.

Em 1995, Thomas Wolff provou que a dimensão Minkowski de um Kakeya ambientado no espaço 3D deve ser de pelo menos 2.5. Esse limite inferior acabou sendo difícil de aumentar. Então, em 1999, os matemáticos Redes Katz, Izabella Laaba e Terence tao conseguiu vencê-lo. Seu novo limite: 2.500000001. Apesar de quão pequena foi a melhoria, ela superou uma enorme barreira teórica. O papel deles era publicado no Anais de Matemática, a revista de maior prestígio da área.

Mais tarde, Katz e Tao esperavam aplicar algumas das ideias desse trabalho para atacar a conjectura 3D Kakeya de uma maneira diferente. Eles levantaram a hipótese de que qualquer contra-exemplo deve ter três propriedades particulares e que a coexistência dessas propriedades deve levar a uma contradição. Se eles pudessem provar isso, isso significaria que a conjectura Kakeya era verdadeira em três dimensões.

Eles não conseguiram ir até o fim, mas fizeram algum progresso. Em particular, eles (juntamente com outros matemáticos) mostraram que qualquer contra-exemplo deve ter duas das três propriedades. Deve ser “plano”, o que significa que sempre que os segmentos de linha se cruzam em um ponto, esses segmentos também estão quase no mesmo plano. Também deve ser “granulado”, o que requer que os planos dos pontos de interseção próximos sejam orientados de maneira semelhante.

Isso deixou a terceira propriedade. Em um conjunto “adesivo”, os segmentos de linha que apontam quase na mesma direção também devem estar localizados próximos uns dos outros no espaço. Katz e Tao não conseguiram provar que todos os contra-exemplos devem ser fixos. Mas, intuitivamente, um conjunto fixo parece ser a melhor maneira de forçar muita sobreposição entre os segmentos de linha, tornando o conjunto o menor possível — exatamente o que você precisa para criar um contra-exemplo. Se alguém pudesse mostrar que um conjunto pegajoso de Kakeya tinha uma dimensão de Minkowski menor que 3, isso refutaria a conjectura 3D de Kakeya. "Parece que 'pegajoso' seria o caso mais preocupante", disse Larry Guth do Instituto de Tecnologia de Massachusetts.

Não é mais uma preocupação.

O ponto crítico

Em 2014 - mais de uma década depois que Katz e Tao tentaram provar a conjectura de Kakeya - Tao postou um esboço de sua abordagem em seu blog, dando a outros matemáticos a chance de experimentá-lo por si mesmos.

Em 2021, Hong Wang, um matemático da Universidade de Nova York, e Josué Zahl da University of British Columbia decidiu continuar de onde Tao e Katz haviam parado.

Eles começaram assumindo a existência de um contra-exemplo pegajoso com uma dimensão de Minkowski menor que 3. Eles sabiam de trabalhos anteriores que tal contra-exemplo tinha que ser plano e granulado. “Então estávamos no tipo de mundo que Terry Tao e Nets Katz estavam pensando”, disse Zahl. Agora eles precisavam mostrar que as propriedades plana, granulada e pegajosa jogavam uma com a outra e levavam a uma contradição, o que significaria que esse contra-exemplo não poderia realmente existir.

Para obter essa contradição, no entanto, Wang e Zahl voltaram sua atenção em uma direção que Katz e Tao não haviam previsto - em direção a uma área conhecida como teoria da projeção.

Eles começaram analisando a estrutura de seu contraexemplo pegajoso com mais detalhes. Se você considerar a versão idealizada do conjunto, ela possui um número infinito de segmentos de linha apontando em todas as direções. Mas, neste problema, lembre-se de que você está lidando com versões maiores desses segmentos de linha — um monte de agulhas. Cada uma dessas agulhas pode conter muitos dos segmentos de linha idealizados, o que significa que você pode codificar todo o conjunto infinito com um número finito de agulhas. Dependendo da espessura das agulhas, seu conjunto gordo pode parecer muito diferente.

Se o conjunto estiver pegajoso, parecerá mais ou menos o mesmo, não importa a espessura das agulhas.

Wang e Zahl usaram essa propriedade para mostrar que, à medida que as agulhas ficam mais finas, o conjunto se torna cada vez mais plano. Por meio desse processo, eles poderiam “extrair um objeto ainda mais patológico”, disse Zahl – algo que parecia ter qualidades impossíveis.

Isso é o que eles mostraram a seguir. Eles provaram que esse objeto patológico tinha que parecer de duas maneiras, ambas levando a contradições. Ou você seria capaz de projetá-lo no espaço 2D de uma forma que o tornasse muito menor em várias direções - algo que Wang e seus colegas acabaram de fazer. mostrou ser impossível. Ou, no segundo caso, as agulhas do conjunto seriam organizadas de acordo com um tipo muito específico de função, que Zahl e seus colaboradores haviam comprovado recentemente. não poderia existir, porque levaria a outros tipos de projeções que não faziam sentido.

Wang e Zahl agora tinham sua contradição - o que significa que não há contra-exemplos rígidos para a conjectura de Kakeya. (Eles mostraram isso não apenas para a dimensão de Minkowski, mas também para uma quantidade relacionada chamada dimensão de Hausdorff.) “O resultado exclui toda essa classe de contra-exemplos”, disse Zahl – o tipo exato de conjunto que os matemáticos consideraram mais provável de refutar. a conjectura.

O novo trabalho “é um forte apoio para a conjectura de Kakeya ser verdadeira”, disse Pablo Shmerkin da Universidade da Colúmbia Britânica. Embora se aplique apenas ao caso tridimensional, algumas de suas técnicas podem ser úteis em dimensões superiores. Depois de passar anos progredindo na conjectura em outros sistemas numéricos, os matemáticos estão entusiasmados com esse retorno ao domínio original do problema dos números reais.

“É notável que eles resolveram este caso completamente”, disse Zhang. “No cenário real, isso é extremamente raro.” E se alguém puder provar que um contra-exemplo deve ser fixo, o novo resultado implicará a conjectura completa em três dimensões. A hierarquia das conjecturas construídas acima dele permanecerá então segura, seu fundamento estável.

“De alguma forma, esses dois problemas diferentes na teoria da projeção, que aparentemente não têm muito a ver um com o outro, se encaixam muito bem para fornecer exatamente o que era necessário para Kakeya”, disse Zahl.