Novo avanço aproxima a multiplicação de matrizes do ideal | Revista Quanta

Os cientistas da computação são um grupo exigente. Para eles, não basta obter a resposta certa para um problema — o objetivo, quase sempre, é obter a resposta da forma mais eficiente possível.

Considere o ato de multiplicar matrizes ou matrizes de números. Em 1812, o matemático francês Jacques Philippe Marie Binet elaborou o conjunto básico de regras que ainda ensinamos aos alunos. Funciona perfeitamente bem, mas outros matemáticos encontraram maneiras de simplificar e acelerar o processo. Agora a tarefa de acelerando o processo da multiplicação de matrizes situa-se na intersecção da matemática e da ciência da computação, onde os investigadores continuam a melhorar o processo até hoje – embora nas últimas décadas os ganhos tenham sido bastante modestos. Desde 1987, as melhorias numéricas na multiplicação de matrizes têm sido “pequenas e… extremamente difíceis de obter”, disse François Le Gall, cientista da computação da Universidade de Nagoya.

Agora, três investigadores – Ran Duan e Renfei Zhou, da Universidade de Tsinghua, e Hongxun Wu, da Universidade da Califórnia, Berkeley – deram um grande passo em frente no ataque a este problema perene. Deles novos resultados, apresentado em novembro passado na conferência Foundations of Computer Science, resulta de uma nova técnica inesperada, disse Le Gall. Embora a melhoria em si tenha sido relativamente pequena, Le Gall a chamou de “conceitualmente maior do que outras anteriores”.

A técnica revela uma fonte até então desconhecida e, portanto, inexplorada de melhorias potenciais, e já deu frutos: Um segundo artigo, publicado em janeiro, baseia-se no primeiro para mostrar como a multiplicação de matrizes pode ser impulsionada ainda mais.

“Este é um grande avanço técnico”, disse William Kuszmaul, um cientista da computação teórico da Universidade de Harvard. “É a maior melhoria na multiplicação de matrizes que vimos em mais de uma década.”

Entre na Matriz

Pode parecer um problema obscuro, mas a multiplicação de matrizes é uma operação computacional fundamental. Ele está incorporado em uma grande proporção dos algoritmos que as pessoas usam todos os dias para uma variedade de tarefas, desde a exibição de gráficos de computador mais nítidos até a solução de problemas logísticos na teoria de redes. E como em outras áreas da computação, a velocidade é fundamental. Mesmo pequenas melhorias podem eventualmente levar a economias significativas de tempo, poder computacional e dinheiro. Mas, por enquanto, os teóricos estão interessados ​​principalmente em descobrir quão rápido o processo pode ser.

A maneira tradicional de multiplicar dois n-A-n matrizes - multiplicando os números de cada linha da primeira matriz pelos números das colunas da segunda - requer n³ multiplicações separadas. Para matrizes 2 por 2, isso significa 2³ ou 8 multiplicações.

Em 1969, o matemático Volker Strassen revelou um procedimento mais complicado que poderia multiplicar matrizes 2 por 2 em apenas sete etapas multiplicativas e 18 adições. Dois anos depois, o cientista da computação Shmuel Winograd demonstrou que sete é, de fato, o mínimo absoluto para matrizes 2 por 2.

Strassen explorou a mesma ideia para mostrar que todos os grandes n-A-n matrizes também podem ser multiplicadas por menos de n³ passos. Um elemento-chave nesta estratégia envolve um procedimento chamado decomposição – quebrar uma grande matriz em submatrizes sucessivamente menores, que podem acabar sendo tão pequenas quanto 2 por 2 ou mesmo 1 por 1 (estes são apenas números únicos).

A justificativa para dividir uma matriz gigante em pequenos pedaços é bastante simples, de acordo com Virgínia Vassilevska Williams, cientista da computação do Instituto de Tecnologia de Massachusetts e coautor de um dos novos artigos. “É difícil para um ser humano olhar para uma matriz grande (digamos, da ordem de 100 por 100) e pensar no melhor algoritmo possível”, disse Vassilevska Williams. Mesmo as matrizes 3 por 3 ainda não foram totalmente resolvidas. “No entanto, pode-se usar um algoritmo rápido que já foi desenvolvido para matrizes pequenas para obter também um algoritmo rápido para matrizes maiores.”

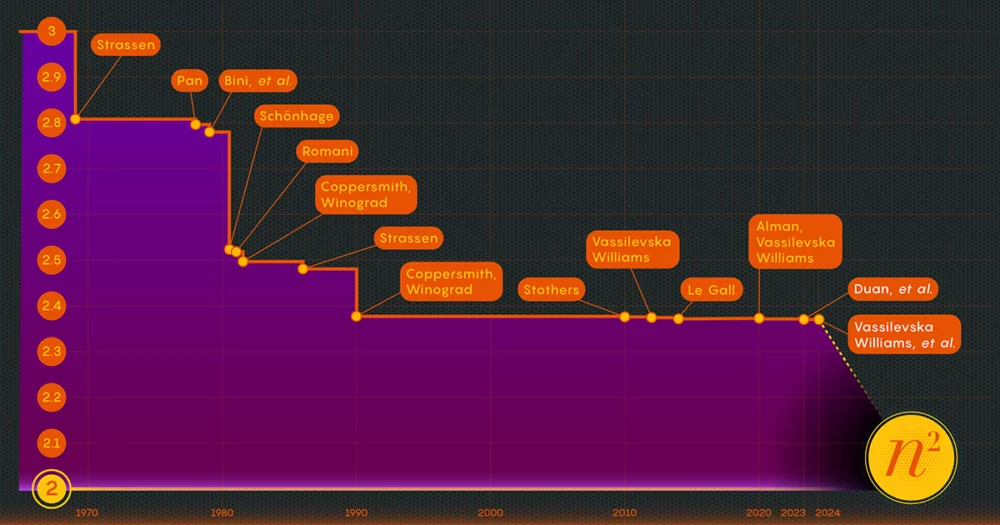
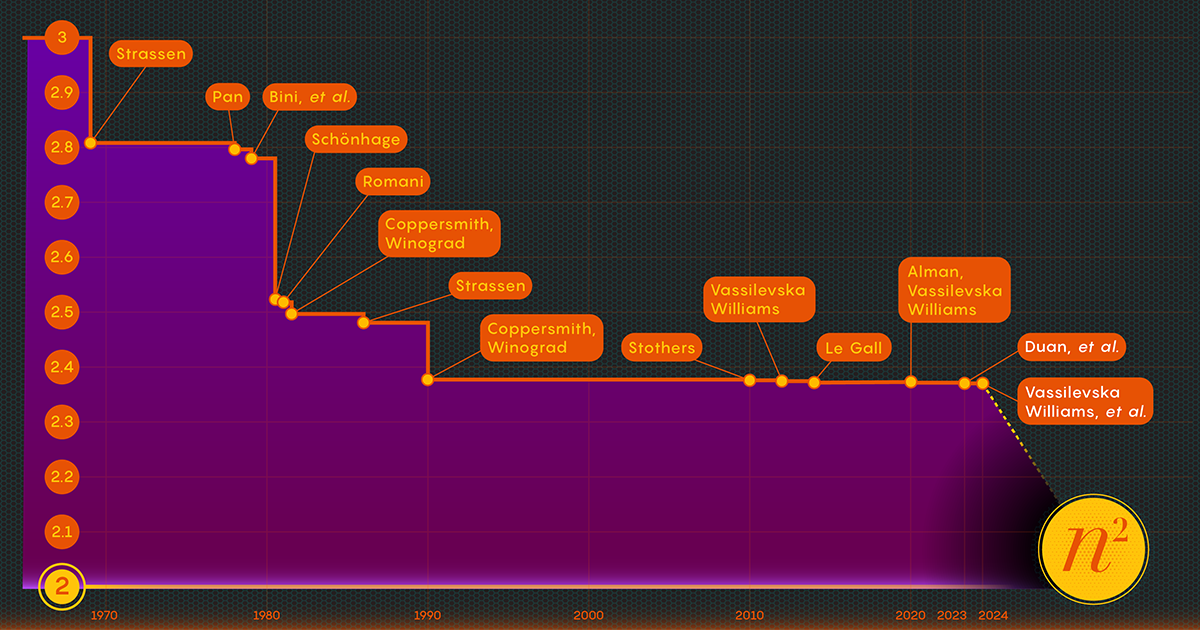
A chave para a velocidade, determinaram os pesquisadores, é reduzir o número de etapas de multiplicação, diminuindo esse expoente de n³ (para o método padrão) tanto quanto puderem. O menor valor possível, n², é basicamente o tempo necessário apenas para escrever a resposta. Os cientistas da computação referem-se a esse expoente como ômega, ω, com n^ω sendo o menor número possível de etapas necessárias para multiplicar com sucesso dois n-A-n matrizes como n cresce muito. “O objetivo deste trabalho”, disse Zhou, que também foi coautor do artigo de janeiro de 2024, “é ver quão perto de 2 podemos chegar e se isso pode ser alcançado em teoria”.

Um foco laser

Em 1986, Strassen teve outro grande avanço quando introduzido o que é chamado de método laser para multiplicação de matrizes. Strassen usou-o para estabelecer um valor superior para ômega de 2.48. Embora o método seja apenas uma etapa em grandes multiplicações de matrizes, é um dos mais importantes porque os pesquisadores continuaram a aprimorá-lo.

Um ano depois, Winograd e Don Coppersmith introduziram um novo algoritmo que complementou lindamente o método do laser. Esta combinação de ferramentas apareceu em praticamente todos os esforços subsequentes para acelerar a multiplicação de matrizes.

Aqui está uma maneira simplificada de pensar sobre como esses diferentes elementos se encaixam. Vamos começar com duas matrizes grandes, A e B, que você deseja multiplicar. Primeiro, você os decompõe em muitas submatrizes menores, ou blocos, como às vezes são chamados. A seguir, você pode usar o algoritmo de Coppersmith e Winograd para servir como uma espécie de manual de instruções para o manuseio e, por fim, a montagem dos blocos. “Isso me diz o que multiplicar e o que adicionar e quais entradas vão para onde” na matriz de produto C, disse Vassilevska Williams. “É apenas uma receita para construir C a partir de A e B.”

Porém, há um problema: às vezes você acaba com blocos que possuem entradas em comum. Deixá-los no produto seria o mesmo que contar essas entradas duas vezes; portanto, em algum momento, você precisará se livrar desses termos duplicados, chamados de sobreposições. Os pesquisadores fazem isso “matando” os blocos em que estão – definindo seus componentes iguais a zero para removê-los do cálculo.

É aí que o método laser de Strassen finalmente entra em ação. “O método do laser normalmente funciona muito bem e geralmente encontra uma boa maneira de eliminar um subconjunto de blocos para remover a sobreposição”, disse Le Gall. Depois que o laser tiver eliminado ou “queimado” todas as sobreposições, você poderá construir a matriz do produto final, C.

Reunir essas várias técnicas resulta em um algoritmo para multiplicar duas matrizes com um número geral deliberadamente mesquinho de multiplicações - pelo menos em teoria. O método a laser não pretende ser prático; é apenas uma forma de pensar sobre a forma ideal de multiplicar matrizes. “Nunca executamos o método [em um computador]”, disse Zhou. “Nós analisamos isso.”

E essa análise foi o que levou à maior melhoria do ômega em mais de uma década.

Uma perda é encontrada

O artigo do Verão passado, escrito por Duan, Zhou e Wu, mostrou que o processo de Strassen ainda poderia ser significativamente acelerado. Tudo por causa de um conceito que eles chamaram de perda oculta, profundamente enterrado em análises anteriores – “resultado de matar muitos blocos involuntariamente”, disse Zhou.

O método laser funciona rotulando os blocos com sobreposições como lixo, destinados ao descarte; outros blocos são considerados dignos e serão salvos. O processo de seleção, no entanto, é um tanto aleatório. Um bloco classificado como lixo pode, na verdade, acabar sendo útil. Isto não foi uma surpresa total, mas ao examinar muitas dessas escolhas aleatórias, a equipe de Duan determinou que o método do laser estava sistematicamente subvalorizando os blocos: mais blocos deveriam ser salvos e menos blocos deveriam ser descartados. E, como normalmente acontece, menos desperdício se traduz em maior eficiência.

“Ser capaz de manter mais blocos sem sobreposição leva a… um algoritmo de multiplicação de matrizes mais rápido”, disse Le Gall.

Depois de comprovar a existência dessa perda, a equipe de Duan modificou a forma como o método a laser rotulava os blocos, reduzindo substancialmente o desperdício. Como resultado, eles estabeleceram um novo limite superior para ômega em torno de 2.371866 – uma melhoria em relação ao limite superior anterior de 2.3728596, ambientado em 2020 por Josh Alman e Vassilevska Williams. Isso pode parecer uma mudança modesta, reduzindo o limite em cerca de 0.001. Mas é a maior melhoria que os cientistas viram desde 2010. O resultado de Vassilevska Williams e Alman em 2020, em comparação, melhorou apenas 0.00001 em relação ao seu antecessor.

Mas o que é mais entusiasmante para os investigadores não é apenas o novo registo em si – que não durou muito. É também o facto de o artigo ter revelado um novo caminho de melhoria que, até então, tinha passado totalmente despercebido. Por quase quatro décadas, todos confiaram no mesmo método de laser, disse Le Gall. “Então eles descobriram que, bem, podemos fazer melhor.”

O artigo de janeiro de 2024 refinou esta nova abordagem, permitindo que Vassilevska Williams, Zhou e seus coautores reduzissem ainda mais a perda oculta. Isto levou a uma melhoria adicional do limite superior do ômega, reduzindo-o para 2.371552. Os autores também generalizaram a mesma técnica para melhorar o processo de multiplicação para retângulos (n-A-m) matrizes — um procedimento que tem aplicações em teoria dos grafos, aprendizado de máquina e outras áreas.

Algum progresso adicional neste sentido é praticamente certo, mas há limites. Em 2015, Le Gall e dois colaboradores provou que a abordagem actual – o método laser juntamente com a receita Coppersmith-Winograd – não pode produzir um ómega abaixo de 2.3078. Para fazer mais melhorias, disse Le Gall, “você precisa melhorar a [abordagem] original de Coppersmith e Winograd, que realmente não mudou desde 1987.. " Mas até agora, ninguém encontrou uma maneira melhor. Pode até não haver um.

“Melhorar o ômega é, na verdade, parte da compreensão desse problema”, disse Zhou. “Se pudermos entender bem o problema, poderemos projetar algoritmos melhores para ele. [E] as pessoas ainda estão nos estágios iniciais de compreensão desse problema antigo.”