Ghid definitiv pentru gruparea K-Means cu Scikit-Learn

Introducere

K-Means clustering este unul dintre cei mai folosiți algoritmi de învățare automată nesupravegheată care formează grupuri de date bazate pe asemănarea dintre instanțele de date.

În acest ghid, vom arunca mai întâi o privire la un exemplu simplu pentru a înțelege cum funcționează algoritmul K-Means înainte de a-l implementa folosind Scikit-Learn. Apoi, vom discuta despre modul de determinare a numărului de clustere (K) în K-Means și, de asemenea, vom acoperi valorile distanței, varianța și K-Means pro și contra.

motivaţia

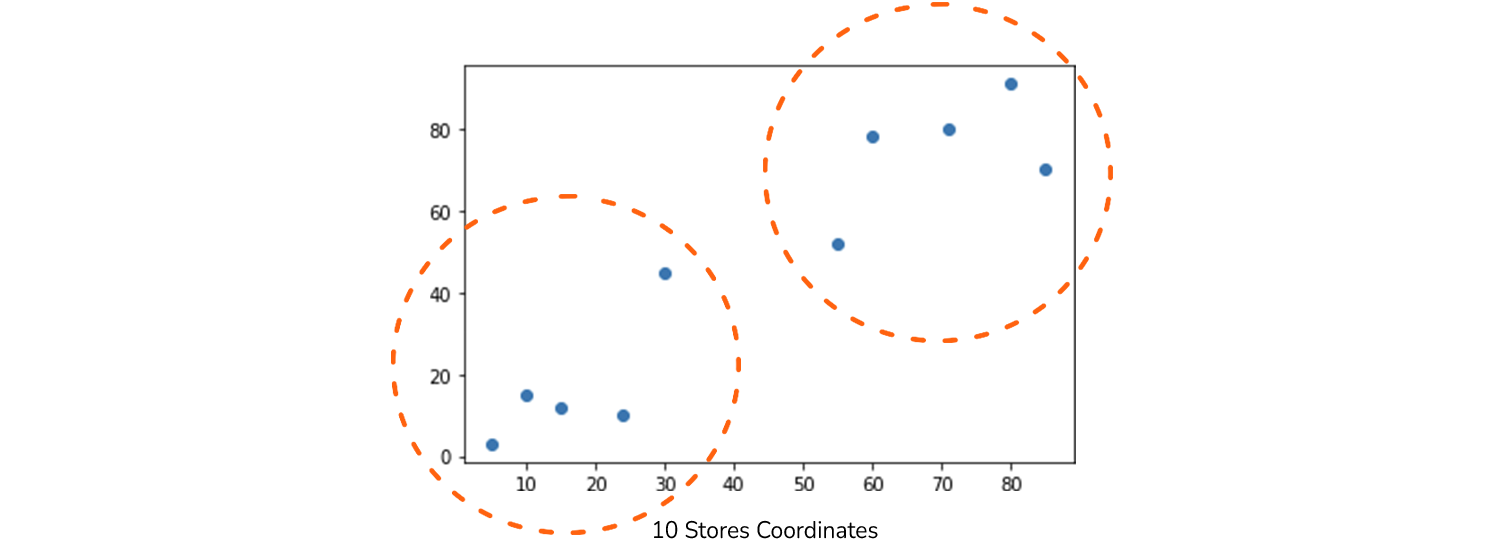
Imaginează-ți următoarea situație. Într-o zi, când te plimbi prin cartier, ai observat că erau 10 magazine de proximitate și ai început să te întrebi care sunt magazinele asemănătoare – mai aproape unele de altele în apropiere. În timp ce căutați modalități de a răspunde la această întrebare, ați întâlnit o abordare interesantă care împarte magazinele în grupuri în funcție de coordonatele lor de pe o hartă.

De exemplu, dacă un magazin a fost situat la 5 km vest și la 3 km nord - ați aloca (5, 3) coordonatele acestuia și reprezentați-l într-un grafic. Să reprezentăm acest prim punct pentru a vizualiza ce se întâmplă:

import matplotlib.pyplot as plt

plt.title("Store With Coordinates (5, 3)")
plt.scatter(x=5, y=3)

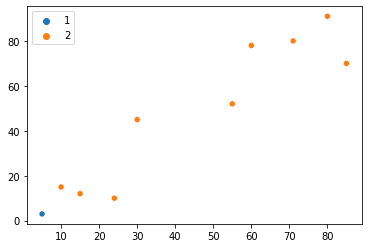
Acesta este doar primul punct, așa că ne putem face o idee despre cum putem reprezenta un magazin. Să spunem că avem deja 10 coordonate pentru cele 10 magazine colectate. După ce le-a organizat într-o numpy matrice, putem, de asemenea, trasa locațiile lor:

import numpy as np

points = np.array([[5, 3], [10, 15], [15, 12], [24, 10], [30, 45], [85, 70], [71, 80], [60, 78], [55, 52],[80, 91]])

xs = points[:,0] 
ys = points[:,1]  

plt.title("10 Stores Coordinates")
plt.scatter(x=xs, y=ys)

Cum să implementați manual algoritmul K-Means

Acum ne putem uita la cele 10 magazine pe un grafic, iar principala problemă este să găsim dacă există o modalitate în care acestea ar putea fi împărțite în diferite grupuri în funcție de proximitate? Doar aruncând o privire rapidă la grafic, probabil vom observa două grupuri de magazine – unul este punctele inferioare din stânga jos, iar celălalt este punctele din dreapta sus. Poate că putem chiar diferenția acele două puncte din mijloc ca un grup separat - prin urmare creând trei grupuri diferite.

În această secțiune, vom trece peste procesul de grupare manuală a punctelor - împărțindu-le în numărul dat de grupuri. În acest fel, vom trece în esență cu atenție peste toate etapele Algoritmul de grupare K-Means. Până la sfârșitul acestei secțiuni, veți obține atât o înțelegere intuitivă, cât și o înțelegere practică a tuturor pașilor efectuati în timpul grupării K-Means. După aceea, îl vom delega către Scikit-Learn.

Care ar fi cel mai bun mod de a determina dacă există două sau trei grupuri de puncte? O modalitate simplă ar fi să alegeți pur și simplu un număr de grupuri – de exemplu, două – și apoi să încercați să grupați puncte pe baza acelei alegeri.

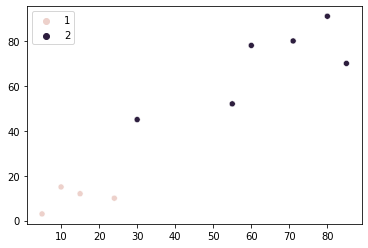
Să presupunem că am decis că există doua grupuri a magazinelor noastre (puncte). Acum, trebuie să găsim o modalitate de a înțelege ce puncte aparțin cărei grupe. Acest lucru se poate face prin alegerea unui punct de reprezentat grupul 1 și unul pentru a reprezenta grupul 2. Aceste puncte vor fi folosite ca referință atunci când se măsoară distanța de la toate celelalte puncte la fiecare grup.

În felul acesta, spuneți punctul (5, 3) ajunge să aparțină grupului 1 și punct (79, 60) la grupul 2. Când se încearcă atribuirea unui nou punct (6, 3) la grupuri, trebuie să îi măsurăm distanța față de aceste două puncte. În cazul punctului (6, 3) is mai aproape la (5, 3), deci aparține grupului reprezentat de punctul respectiv – grupul 1. În acest fel, putem grupa cu ușurință toate punctele în grupuri corespunzătoare.

În acest exemplu, pe lângă determinarea numărului de grupuri (clustere) – alegem și câteva puncte pentru a fi a referință de distanță pentru puncte noi din fiecare grupă.

Aceasta este ideea generală de a înțelege asemănările dintre magazinele noastre. Să o punem în practică – putem alege mai întâi cele două puncte de referință la aleator. Punctul de referință al grupul 1 va fi (5, 3) si punctul de referinta al grupul 2 va fi (10, 15). Putem selecta ambele puncte ale noastre numpy matrice de [0] și [1] indexează și le stochează în g1 (grupa 1) și g2 (grupul 2) variabile:

g1 = points[0]
g2 = points[1]

După ce facem acest lucru, trebuie să calculăm distanța de la toate celelalte puncte la acele puncte de referință. Acest lucru ridică o întrebare importantă - cum să măsurați distanța. În esență, putem folosi orice măsură de distanță, dar, în scopul acestui ghid, să folosim Euclidean Distance_.

Poate fi util să știm că măsura euclidiană a distanței se bazează pe teorema lui Pitagora:

$$
c^2 = a^2 + b^2
$$

Când este adaptat la punctele din avion - (a1, b1) și (a2, b2), formula anterioară devine:

$$
c^2 = (a2-a1)^2 + (b2-b1)^2
$$

Distanța va fi rădăcina pătrată a c, deci putem scrie formula ca:

$$
euclidian_{dist} = sqrt[2][(a2 – a1)^2 + (b2 – b1) ^2)]
$$

Până acum, am ales punctele pentru a reprezenta grupuri și știm să calculăm distanțele. Acum, să punem împreună distanțele și grupurile, atribuind fiecăruia dintre punctele noastre de magazin colectate unui grup.

Pentru a vizualiza mai bine acest lucru, vom declara trei liste. Primul care stochează puncte din primul grup - points_in_g1. Al doilea pentru a stoca puncte din grupa 2 – points_in_g2, Și ultimul - group, Pentru a etichetă punctele ca fie 1 (aparține grupului 1) sau 2 (aparține grupului 2):

points_in_g1 = []
points_in_g2 = []
group = []

Acum putem itera punctele noastre și calcula distanța euclidiană dintre ele și fiecare dintre referințele noastre de grup. Fiecare punct va fi mai aproape la unul dintre cele două grupuri – în funcție de grupul cel mai apropiat, vom atribui fiecare punct listei corespunzătoare, adăugând totodată 1 or 2 la group listă:

for p in points:
    x1, y1 = p[0], p[1]
    euclidean_distance_g1 = np.sqrt((g1[0] - x1)**2 + (g1[1] - y1)**2)
    euclidean_distance_g2 = np.sqrt((g2[0] - x1)**2 + (g2[1] - y1)**2)
    if euclidean_distance_g1 < euclidean_distance_g2:
        points_in_g1.append(p)
        group.append('1')
    else:
        points_in_g2.append(p)
        group.append('2')

Să ne uităm la rezultatele acestei iterații pentru a vedea ce s-a întâmplat:

print(f'points_in_g1:{points_in_g1}n 
npoints_in_g2:{points_in_g2}n 
ngroup:{group}')

Ceea ce are ca rezultat:

points_in_g1:[array([5, 3])]
 
points_in_g2:[array([10, 15]), array([15, 12]), 
              array([24, 10]), array([30, 45]), 
              array([85, 70]), array([71, 80]),
              array([60, 78]), array([55, 52]), 
              array([80, 91])]
 
group:[1, 2, 2, 2, 2, 2, 2, 2, 2, 2] 

De asemenea, putem reprezenta un grafic rezultatul grupării, cu culori diferite în funcție de grupurile alocate, folosind Seaborn's scatterplot() cu group ca o hue argument:

import seaborn as sns

sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

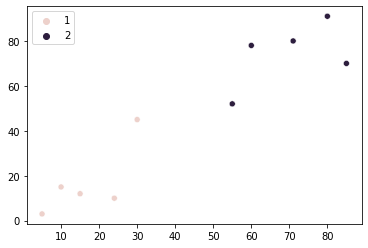
Este clar că doar primul nostru punct este alocat grupului 1, iar toate celelalte puncte au fost atribuite grupului 2. Acest rezultat diferă de ceea ce ne-am imaginat la început. Având în vedere diferența dintre rezultatele noastre și așteptările noastre inițiale – există vreo modalitate de a schimba asta? Se pare că există!

O abordare este de a repeta procesul și de a alege diferite puncte pentru a fi referințele grupurilor. Acest lucru ne va schimba rezultatele, sperăm, mai mult în concordanță cu ceea ce ne-am imaginat la început. De a doua oară, le-am putea alege nu la întâmplare, așa cum am făcut anterior, ci obținând un însemna dintre toate punctele noastre deja grupate. Astfel, acele noi puncte ar putea fi poziționate în mijlocul grupurilor corespunzătoare.

De exemplu, dacă al doilea grup avea doar puncte (10, 15), (30, 45). Noul central punctul ar fi (10 + 30)/2 și (15+45)/2 – care este egal cu (20, 30).

Deoarece ne-am pus rezultatele în liste, le putem converti mai întâi în numpy matrice, selectați-le xs, ys și apoi obțineți însemna:

g1_center = [np.array(points_in_g1)[:, 0].mean(), np.array(points_in_g1)[:, 1].mean()]
g2_center = [np.array(points_in_g2)[:, 0].mean(), np.array(points_in_g2)[:, 1].mean()]
g1_center, g2_center

Pentru a ajuta la repetarea procesului cu noile noastre puncte centrale, să transformăm codul nostru anterior într-o funcție, să-l executăm și să vedem dacă au existat modificări în modul în care sunt grupate punctele:

def assigns_points_to_two_groups(g1_center, g2_center):
    points_in_g1 = []
    points_in_g2 = []
    group = []

    for p in points:
        x1, y1 = p[0], p[1]
        euclidean_distance_g1 = np.sqrt((g1_center[0] - x1)**2 + (g1_center[1] - y1)**2)
        euclidean_distance_g2 = np.sqrt((g2_center[0] - x1)**2 + (g2_center[1] - y1)**2)
        if euclidean_distance_g1 < euclidean_distance_g2:
            points_in_g1.append(p)
            group.append(1)
        else:
            points_in_g2.append(p)
            group.append(2)
    return points_in_g1, points_in_g2, group

Să apelăm funcția și să-i stocăm rezultatele în points_in_g1, points_in_g2, și group variabile:

points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
points_in_g1, points_in_g2, group

Și, de asemenea, trasați graficul de dispersie cu punctele colorate pentru a vizualiza diviziunea grupurilor:

sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

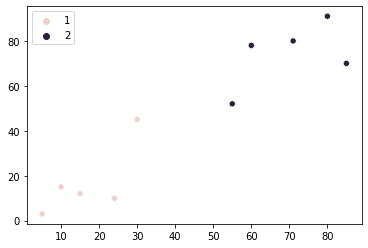
Se pare că gruparea punctelor noastre este a se imbunatati. Dar totuși, există două puncte în mijlocul graficului care ar putea fi atribuite oricărui grup atunci când se ia în considerare apropierea lor de ambele grupuri. Algoritmul pe care l-am dezvoltat până acum atribuie ambele puncte celui de-al doilea grup.

Aceasta înseamnă că probabil că putem repeta procesul încă o dată, luând mijloacele X și Y, creând două noi puncte centrale. (centroizi) grupurilor noastre și reatribuind-le în funcție de distanță.

Să creăm și o funcție pentru a actualiza centroizii. Întregul proces acum poate fi redus la apeluri multiple ale acelei funcții:

def updates_centroids(points_in_g1, points_in_g2):
    g1_center = np.array(points_in_g1)[:, 0].mean(), np.array(points_in_g1)[:, 1].mean()
    g2_center = np.array(points_in_g2)[:, 0].mean(), np.array(points_in_g2)[:, 1].mean()
    return g1_center, g2_center

g1_center, g2_center = updates_centroids(points_in_g1, points_in_g2)
points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

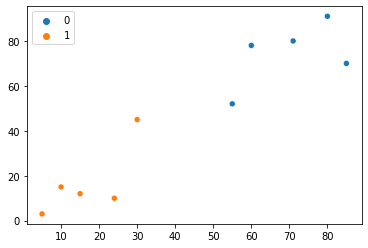
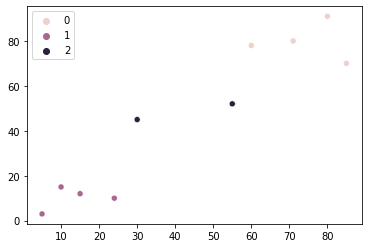
Observați că după această a treia iterație, fiecare dintre puncte aparține acum unor grupuri diferite. Se pare că rezultatele sunt din ce în ce mai bune – hai să o facem încă o dată. Acum mergi la a patra iterație a metodei noastre:

g1_center, g2_center = updates_centroids(points_in_g1, points_in_g2)
points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

De a patra oară am primit acelasi rezultat ca si precedenta. Deci, se pare că punctele noastre nu vor mai schimba grupurile, rezultatul nostru a atins un fel de stabilitate – a ajuns într-o stare de neschimbat, sau convergentă. Pe lângă asta, avem exact același rezultat pe care ne-am imaginat-o pentru cele 2 grupe. De asemenea, putem vedea dacă această diviziune atinsă are sens.

Să recapitulăm rapid ceea ce am făcut până acum. Ne-am împărțit cele 10 magazine din punct de vedere geografic în două secțiuni – una în regiunile inferioare de sud-vest și altele în nord-est. Poate fi interesant să strângem mai multe date în afară de ceea ce avem deja – venituri, numărul zilnic de clienți și multe altele. În acest fel, putem efectua o analiză mai bogată și, eventual, putem genera rezultate mai interesante.

Astfel de studii de grupare pot fi efectuate atunci când un brand deja stabilit dorește să aleagă o zonă pentru a deschide un nou magazin. În acest caz, există mult mai multe variabile luate în considerare în afară de locație.

Ce legătură au toate acestea cu algoritmul K-Means?

În timp ce urmați acești pași, s-ar putea să vă întrebați ce legătură au ei cu algoritmul K-Means. Procesul pe care l-am condus până acum este Algoritmul K-Means. Pe scurt, am determinat numărul de grupuri/clustere, am ales aleatoriu punctele inițiale și am actualizat centroizii în fiecare iterație până când clusterele au convergit. Practic, am executat întreg algoritmul manual – efectuând cu atenție fiecare pas.

K în K-Means vine de la numărul de clustere care trebuie setate înainte de a începe procesul de iterație. În cazul nostru K = 2. Această caracteristică este uneori văzută ca negativ având în vedere că există și alte metode de clustering, cum ar fi Ierarhical Clustering, care nu trebuie să aibă un număr fix de clustere în prealabil.

Datorită utilizării mijloacelor, K-means devine și sensibil la valori aberante și la valori extreme – ele sporesc variabilitatea și îngreunează ca centroizii noștri să își joace rolul. Deci, fii conștient de necesitatea de a face performanță valori extreme și analize aberante înainte de a efectua o grupare folosind algoritmul K-Means.

De asemenea, observați că punctele noastre au fost segmentate în părți drepte, nu există curbe la crearea clusterelor. Acesta poate fi, de asemenea, un dezavantaj al algoritmului K-Means.

K-Means are și multe Avantajele! Se comporta bine pe seturi de date mari care poate deveni dificil de gestionat dacă utilizați unele tipuri de algoritmi de grupare ierarhică. De asemenea garantează convergența, și poate cu ușurință generaliza și adapta. Pe lângă asta, este probabil cel mai folosit algoritm de clustering.

Acum că am trecut peste toți pașii efectuati în algoritmul K-Means și am înțeles toate avantajele și dezavantajele acestuia, putem în sfârșit să implementăm K-Means folosind biblioteca Scikit-Learn.

Cum să implementați algoritmul K-Means folosind Scikit-Learn

Pentru a verifica de două ori rezultatul nostru, să facem acest proces din nou, dar acum folosind 3 linii de cod cu sklearn:

from sklearn.cluster import KMeans


kmeans = KMeans(n_clusters=2, random_state=42) 
kmeans.fit(points)
kmeans.labels_

Aici, etichetele sunt aceleași cu grupurile noastre anterioare. Să reprezentăm rapid rezultatul:

sns.scatterplot(x = points[:,0], y = points[:,1], hue=kmeans.labels_)

Graficul rezultat este același cu cel din secțiunea anterioară.

Cu Scikit-Learn, puteți, de asemenea, să inițializați K-Means pentru o convergență mai rapidă, setând init='k-means++' argument. În termeni mai largi, K-Means++ încă alege k clusterul inițial se centrează la întâmplare urmând o distribuție uniformă. Apoi, fiecare centru de cluster ulterior este ales dintre punctele de date rămase nu prin calcularea doar a unei măsuri de distanță, ci prin utilizarea probabilității. Utilizarea probabilității accelerează algoritmul și este utilă atunci când aveți de-a face cu seturi de date foarte mari.

Metoda cotului – Alegerea celui mai bun număr de grupuri

Până acum, bine! Am grupat 10 magazine pe baza distanței euclidiene dintre puncte și centroizi. Dar cum rămâne cu acele două puncte din mijlocul graficului care sunt puțin mai greu de grupat? Nu ar putea forma și ei un grup separat? Chiar am făcut o greșeală alegând? K = 2 grupuri? Poate chiar am avut K = 3 grupuri? Am putea chiar să avem mai mult de trei grupuri și să nu fim conștienți de asta.

Întrebarea care se pune aici este cum se determină numărul de grupuri (K) în K-Means. Pentru a răspunde la această întrebare, trebuie să înțelegem dacă ar exista un cluster „mai bun” pentru o valoare diferită a lui K.

Modul naiv de a afla acest lucru este prin gruparea punctelor cu diferite valori ale K, prin urmare K=2, K=3, K=4 și așa mai departe:

for number_of_clusters in range(1, 11): 
    kmeans = KMeans(n_clusters = number_of_clusters, random_state = 42)
    kmeans.fit(points) 

Dar, puncte de grupare pentru diferite Ks singur nu va fi suficient pentru a înțelege dacă am ales valoarea ideală pentru K. Avem nevoie de o modalitate de a evalua calitatea grupării pentru fiecare K noi am ales.

Calcularea manuală a În cadrul grupului Suma pătratelor (WCSS)

Aici este locul ideal pentru a introduce o măsură a cât de mult sunt punctele noastre grupate aproape unele de altele. În esență, descrie cât de mult dezacord avem în interiorul unui singur cluster. Această măsură se numește În cadrul clusterului Suma pătratelor, Sau WCSS pe scurt. Cu cât WCSS este mai mic, cu atât punctele noastre sunt mai apropiate, prin urmare avem un cluster mai bine format. Formula WCSS poate fi utilizată pentru orice număr de clustere:

$$
WCSS = sum(Pi_1 – Centroid_1)^2 + cdots + sum(Pi_n – Centroid_n)^2
$$

Acum putem presupune că am optat să avem două clustere și să încercăm să implementăm WCSS pentru a înțelege mai bine ce este WCSS și cum să îl folosim. După cum afirmă formula, trebuie să însumăm diferențele pătrate dintre toate punctele cluster și centroizii. Deci, dacă primul nostru punct din primul grup este (5, 3) iar ultimul nostru centroid (după convergență) al primului grup este (16.8, 17.0), WCSS va fi:

$$
WCSS = suma((5,3) – (16.8, 17.0))^2
$$

$$
WCSS = suma((5-16.8) + (3-17.0))^2
$$

$$
WCSS = suma((-11.8) + (-14.0))^2
$$

$$
WCSS = suma((-25.8))^2
$$

$$
WCSS = 335.24
$$

Acest exemplu ilustrează modul în care calculăm WCSS pentru un punct din cluster. Dar clusterul conține de obicei mai mult de un punct și trebuie să le luăm în considerare pe toate atunci când calculăm WCSS. Vom face asta prin definirea unei funcții care primește un grup de puncte și centroizi și returnează suma pătratelor:

def sum_of_squares(cluster, centroid):
    squares = []
    for p in cluster:
        squares.append((p - centroid)**2)
        ss = np.array(squares).sum()
    return ss

Acum putem obține suma pătratelor pentru fiecare grup:

g1 = sum_of_squares(points_in_g1, g1_center)
g2 = sum_of_squares(points_in_g2, g2_center)

Și însumați rezultatele pentru a obține totalul WCSS:

g1 + g2

Rezultă:

2964.3999999999996

Deci, în cazul nostru, când K este egal cu 2, WCSS total este 2964.39. Acum, putem schimba K și calcula WCSS pentru toate. În acest fel, putem obține o perspectivă asupra a ceea ce K ar trebui să alegem să facem ca clusteringul nostru să funcționeze cel mai bine.

De calculat WCSS Utilizarea Scikit-Learn

Din fericire, nu trebuie să calculăm manual WCSS pentru fiecare K. După efectuarea grupării K-Means pentru un număr dat de clustere, putem obține WCSS-ul său folosind inertia_ atribut. Acum, ne putem întoarce la K-Means for buclă, utilizați-o pentru a schimba numărul de clustere și pentru a enumera valorile WCSS corespunzătoare:

wcss = [] 
for number_of_clusters in range(1, 11): 
    kmeans = KMeans(n_clusters = number_of_clusters, random_state = 42)
    kmeans.fit(points) 
    wcss.append(kmeans.inertia_)
wcss

Observați că a doua valoare din listă este exact aceeași pentru care am calculat-o înainte K = 2:

[18272.9, # For k=1 
 2964.3999999999996, # For k=2
 1198.75, # For k=3
 861.75,
 570.5,
 337.5,
 175.83333333333334,
 79.5,
 17.0,
 0.0]

Pentru a vizualiza aceste rezultate, haideți să facem un grafic Ks împreună cu valorile WCSS:

ks = [1, 2, 3, 4, 5 , 6 , 7 , 8, 9, 10]
plt.plot(ks, wcss)

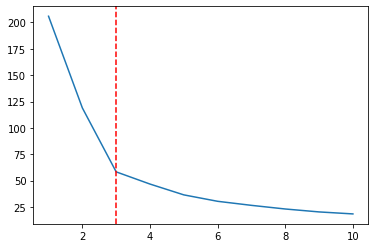
Există o întrerupere pe un complot când x = 2, un punct scăzut în linie și unul chiar mai jos când x = 3. Observați că ne amintește de forma unui cot. Prin trasarea K-urilor împreună cu WCSS, folosim Metoda cotului pentru a alege numărul de Ks. Si K ales este exact cel mai jos punct de cot, deci, ar fi 3 în loc de 2, în cazul nostru:

ks = [1, 2, 3, 4, 5 , 6 , 7 , 8, 9, 10]
plt.plot(ks, wcss);
plt.axvline(3, linestyle='--', color='r')

Putem rula din nou algoritmul cluster K-Means, pentru a vedea cum ar arăta datele noastre trei clustere:

kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(points)
sns.scatterplot(x = points[:,0], y = points[:,1], hue=kmeans.labels_)

Eram deja mulțumiți de două clustere, dar conform metodei cotului, trei clustere s-ar potrivi mai bine pentru datele noastre. În acest caz, am avea trei tipuri de magazine în loc de două. Înainte de a folosi metoda cotului, ne-am gândit la grupuri de magazine de sud-vest și nord-est, acum avem și magazine în centru. Poate că aceasta ar putea fi o locație bună pentru a deschide un alt magazin, deoarece ar avea mai puțină concurență în apropiere.

Măsuri alternative de calitate a clusterului

Există și alte măsuri care pot fi utilizate la evaluarea calității clusterului:

• Scor Silhouette – analizează nu numai distanța dintre punctele intra-cluster, ci și între grupurile în sine
• Între clustere Suma pătratelor (BCSS) – metrica complementară WCSS
• Eroare suma pătratelor (ESS)
• Raza maximă – măsoară cea mai mare distanță de la un punct la centrul său de centru
• Raza medie – suma celei mai mari distanțe de la un punct la centrul său de centru împărțită la numărul de clustere.

Este recomandat să experimentați și să le cunoașteți pe fiecare, deoarece, în funcție de problemă, unele dintre alternative pot fi mai aplicabile decât cele mai utilizate valori. (WCSS și Silhouette Score).

În cele din urmă, ca și în cazul multor algoritmi de știință a datelor, dorim să reducem varianța în interiorul fiecărui cluster și să maximizăm varianța dintre diferitele clustere. Deci avem clustere mai definite și separabile.

Aplicarea K-Means pe un alt set de date

Să folosim ceea ce am învățat pe alt set de date. De data aceasta, vom încerca să găsim grupuri de vinuri similare.

Începem prin a importa pandas pentru a citi wine-clustering CSV (Valori separate prin virgulă) dosar într-un Dataframe structura:

import pandas as pd

df = pd.read_csv('wine-clustering.csv')

După ce îl încărcăm, să aruncăm o privire la primele cinci înregistrări de date cu head() metodă:

df.head()

Rezultă:

	Alcohol 	Malic_Acid 	Ash 	Ash_Alcanity 	Magnesium 	Total_Phenols 	Flavanoids 	Nonflavanoid_Phenols 	Proanthocyanins 	Color_Intensity 	Hue 	OD280 	Proline
0 	14.23 		1.71 		2.43 	15.6 			127 		2.80 			3.06 		0.28 					2.29 				5.64 				1.04 	3.92 	1065
1 	13.20 		1.78 		2.14 	11.2 			100 		2.65 			2.76 		0.26 					1.28 				4.38 				1.05 	3.40 	1050
2 	13.16 		2.36 		2.67 	18.6 			101 		2.80 			3.24 		0.30 					2.81 				5.68 				1.03 	3.17 	1185
3 	14.37 		1.95 		2.50 	16.8 			113 		3.85 			3.49 		0.24 					2.18 				7.80 				0.86 	3.45 	1480
4 	13.24 		2.59 		2.87 	21.0 			118 		2.80 			2.69 		0.39 					1.82 				4.32 				1.04 	2.93 	735

Avem multe măsurători ale substanțelor prezente în vinuri. Aici, de asemenea, nu va trebui să transformăm coloanele categorice, deoarece toate sunt numerice. Acum, să aruncăm o privire la statisticile descriptive cu describe() metodă:

df.describe().T 

Tabelul descris:

 						count 	mean 		std 		min 	25% 	50% 	75% 		max
Alcohol 				178.0 	13.000618 	0.811827 	11.03 	12.3625 13.050 	13.6775 	14.83
Malic_Acid 				178.0 	2.336348 	1.117146 	0.74 	1.6025 	1.865 	3.0825 		5.80
Ash 					178.0 	2.366517 	0.274344 	1.36 	2.2100 	2.360 	2.5575 		3.23
Ash_Alcanity 			178.0 	19.494944 	3.339564 	10.60 	17.2000 19.500 	21.5000 	30.00
Magnesium 				178.0 	99.741573 	14.282484 	70.00 	88.0000 98.000 	107.0000 	162.00
Total_Phenols 			178.0 	2.295112 	0.625851 	0.98 	1.7425 	2.355 	2.8000 		3.88
Flavanoids 				178.0 	2.029270 	0.998859 	0.34 	1.2050 	2.135 	2.8750 		5.08
Nonflavanoid_Phenols 	178.0 	0.361854 	0.124453 	0.13 	0.2700 	0.340 	0.4375 		0.66
Proanthocyanins 		178.0 	1.590899 	0.572359 	0.41 	1.2500 	1.555 	1.9500 		3.58
Color_Intensity 		178.0 	5.058090 	2.318286 	1.28 	3.2200 	4.690 	6.2000 		13.00
Hue 					178.0 	0.957449 	0.228572 	0.48 	0.7825 	0.965 	1.1200 		1.71
OD280 					178.0 	2.611685 	0.709990 	1.27 	1.9375 	2.780 	3.1700 		4.00
Proline 				178.0 	746.893258 	314.907474 	278.00 	500.500 673.500 985.0000 	1680.00

Privind la masă, este clar că există unele variabilitate a datelor – pentru unele coloane precum Alchool există mai multe, iar pentru altele, precum Malic_Acid, Mai puțin. Acum putem verifica dacă există null, Sau NaN valorile din setul nostru de date:

df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 178 entries, 0 to 177
Data columns (total 13 columns):
 #   Column                Non-Null Count  Dtype  
---  ------                --------------  -----  
 0   Alcohol               178 non-null    float64
 1   Malic_Acid            178 non-null    float64
 2   Ash                   178 non-null    float64
 3   Ash_Alcanity          178 non-null    float64
 4   Magnesium             178 non-null    int64  
 5   Total_Phenols         178 non-null    float64
 6   Flavanoids            178 non-null    float64
 7   Nonflavanoid_Phenols  178 non-null    float64
 8   Proanthocyanins       178 non-null    float64
 9   Color_Intensity       178 non-null    float64
 10  Hue                   178 non-null    float64
 11  OD280                 178 non-null    float64
 12  Proline               178 non-null    int64  
dtypes: float64(11), int64(2)
memory usage: 18.2 KB

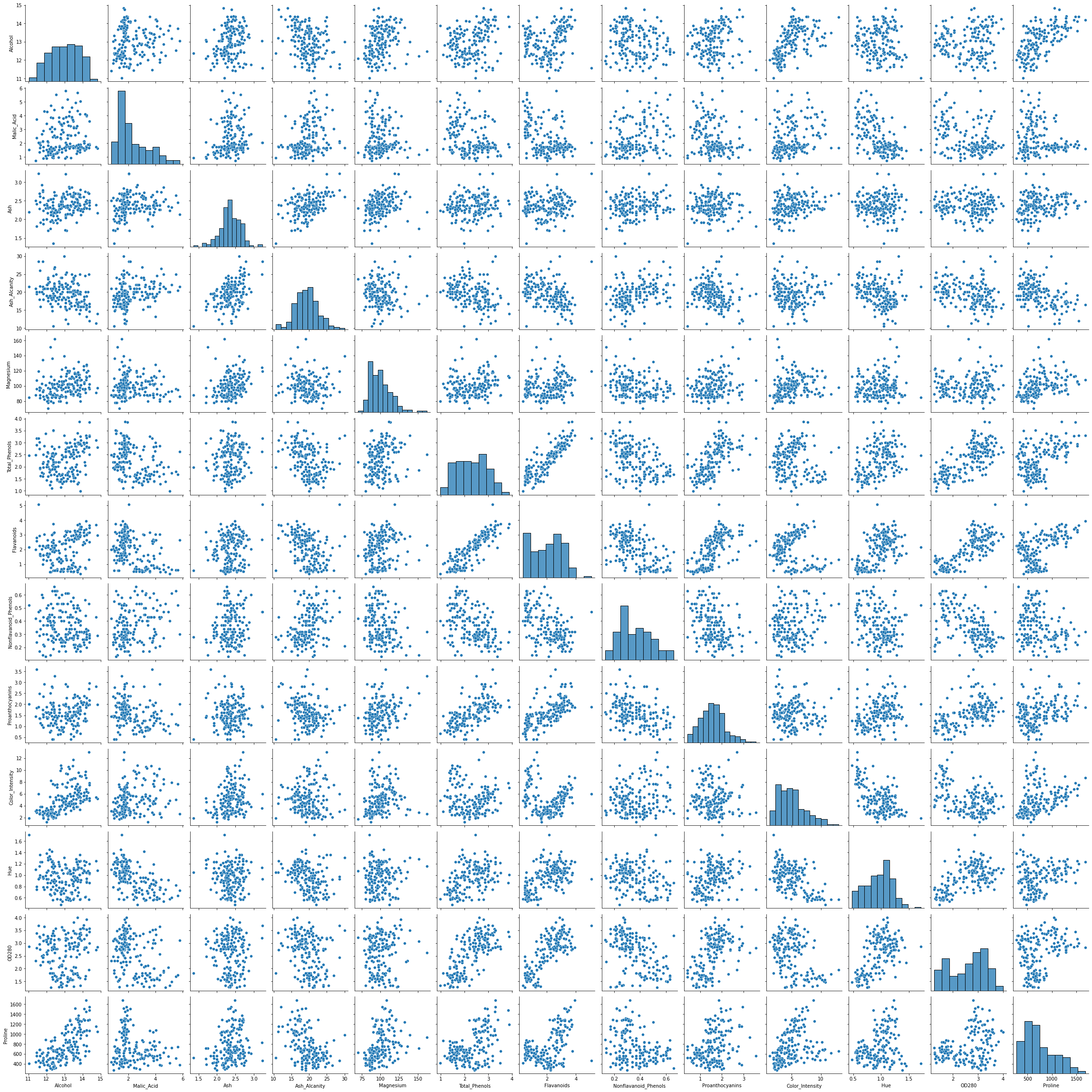
Nu este nevoie să aruncați sau să introduceți date, având în vedere că nu există valori goale în setul de date. Putem folosi un Seaborn pairplot() pentru a vedea distribuția datelor și pentru a verifica dacă setul de date formează perechi de coloane care pot fi interesante pentru grupare:

sns.pairplot(df)

Privind diagrama perechilor, două coloane par promițătoare în scopuri de grupare - Alcohol și OD280 (care este o metodă de determinare a concentrației de proteine ​​din vinuri). Se pare că există 3 grupuri distincte pe parcele care combină două dintre ele.

Există și alte coloane care par a fi în corelație. Mai ales Alcohol și Total_Phenols, și Alcohol și Flavanoids. Au relații liniare mari care pot fi observate în diagrama perechilor.

Deoarece focalizarea noastră este gruparea cu K-Means, să alegem o pereche de coloane, să zicem Alcohol și OD280și testați metoda cotului pentru acest set de date.

Să trasăm graficul de dispersie cu cele două coloane setate să fie axa sa pentru a arunca o privire mai atentă asupra punctelor pe care dorim să le împărțim în grupuri:

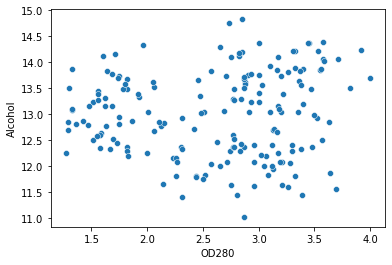
sns.scatterplot(data=df, x='OD280', y='Alcohol')

Acum ne putem defini coloanele și folosim metoda cotului pentru a determina numărul de clustere. Vom iniția și algoritmul cu kmeans++ doar pentru a te asigura că converge mai repede:

values = df[['OD280', 'Alcohol']]

wcss_wine = [] 
for i in range(1, 11): 
    kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
    kmeans.fit(values) 
    wcss_wine.append(kmeans.inertia_)

Am calculat WCSS, astfel încât să putem reprezenta grafic rezultatele:

clusters_wine = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
plt.plot(clusters_wine, wcss_wine)
plt.axvline(3, linestyle='--', color='r')

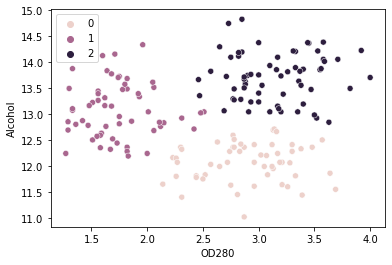
Conform metodei cotului ar trebui să avem 3 ciorchini aici. Pentru pasul final, să ne grupăm punctele în 3 grupuri și să reprezentăm acele grupuri identificate prin culori:

kmeans_wine = KMeans(n_clusters=3, random_state=42)
kmeans_wine.fit(values)
sns.scatterplot(x = values['OD280'], y = values['Alcohol'], hue=kmeans_wine.labels_)

Putem vedea clustere 0, 1, și 2 în grafic. Pe baza analizei noastre, grupul 0 are vinuri cu conținut mai mare de proteine ​​și alcool mai scăzut, grupul 1 are vinuri cu conținut mai mare de alcool și cu conținut scăzut de proteine, și grupul 2 are în vinuri atât un conținut ridicat de proteine, cât și un nivel ridicat de alcool.

Acesta este un set de date foarte interesant și vă încurajez să mergeți mai departe în analiză prin gruparea datelor după normalizare și PCA - de asemenea, prin interpretarea rezultatelor și găsirea de noi conexiuni.

Concluzie

K-înseamnă clustering-ul este un algoritm de învățare automată nesupravegheat simplu, dar foarte eficient pentru gruparea datelor. Acesta grupează datele pe baza distanței euclidiene dintre punctele de date. Algoritmul de grupare K-Means are multe utilizări pentru gruparea documentelor text, imagini, videoclipuri și multe altele.