Združevanje polj, matematiki gredo daleč od starega problema | Revija Quanta

Sprememba načrtov je prišla na potovanju. Na lep dan lanskega aprila so matematiki Rachel Greenfeld in Sarah Peluse sta se odpravila iz domače ustanove, Inštituta za napredne študije v Princetonu v New Jerseyju, v Rochester v New Yorku, kjer naj bi imela oba naslednji dan predavanja.

Skoraj dve leti so se borili s pomembno domnevo v harmonični analizi, področju, ki preučuje, kako kompleksne signale razstaviti na njihove sestavne frekvence. Skupaj s tretjim sodelavcem je Marina Iliopoulou, sta preučevala različico problema, v kateri so frekvence komponent predstavljene kot točke v ravnini, katerih medsebojne razdalje so povezane s celimi števili. Trije raziskovalci so skušali pokazati, da teh točk ne more biti preveč, vendar so bile doslej vse njihove tehnike neučinkovite.

Zdelo se je, kot da se vrtijo. Potem je Peluse pomislil: Kaj če bi opustili problem harmonične analize - seveda začasno - in svojo pozornost usmerili na nize točk, v katerih je razdalja med katerima koli točkama natančno celo število? Kakšne možne strukture imajo lahko takšne množice? Matematiki že od antičnih časov poskušajo razumeti nize celih razdalj. Na primer, pitagorejske trojke (kot so 3, 4 in 5) predstavljajo pravokotne trikotnike, katerih tri oglišča so med seboj oddaljena cela števila.

"V avtu, ker je bila Rachel ujeta z menoj, sem to omenil," je dejal Peluse, ki je zdaj profesor na Univerzi v Michiganu. Zamisel o reševanju celoštevilske razdalje naelektri Greenfelda.

Preden so se zavedli, so se lotili ne ene spremembe smeri, temveč dveh.

»Pravzaprav smo prenehali biti pozorni na to, kam gremo, in nismo zapustili hitre ceste,« je dejal Peluse. "Šli smo v nasprotni smeri iz Rochesterja približno eno uro, preden smo opazili, ker smo bili tako navdušeni nad matematiko."

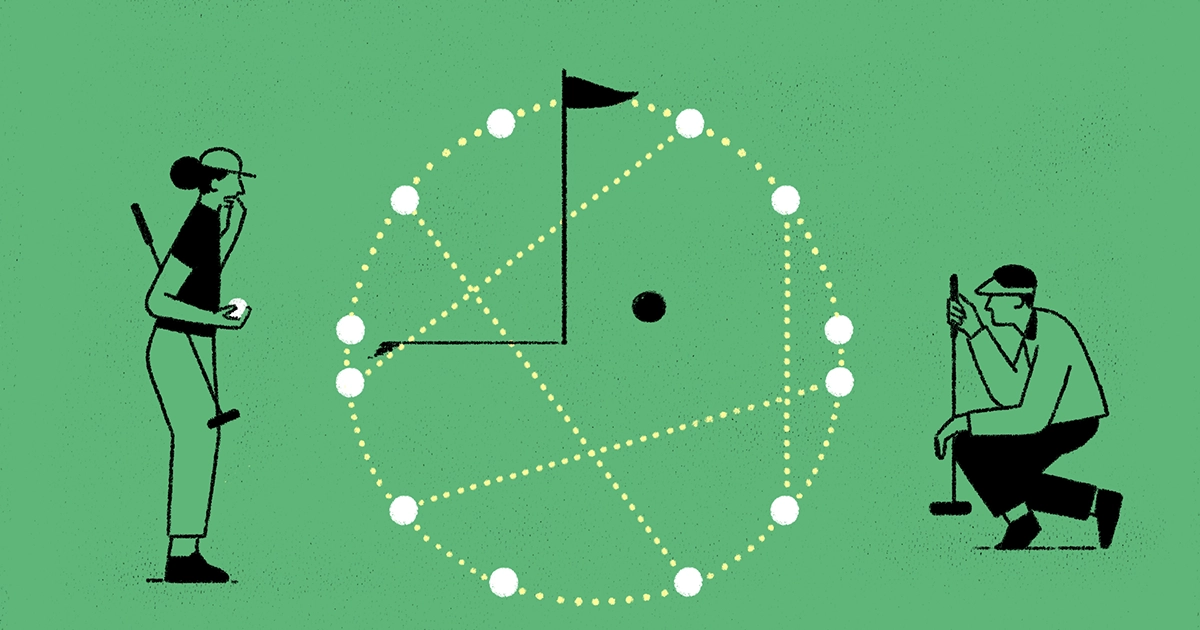
Leta 1945 Norman Anning in Paul Erdős dokazano da mora na premici ležati neskončna množica točk v ravnini, ki so med seboj oddaljene celo število. Za končno množico točk so možnosti nekoliko bolj raznolike. Matematiki so izdelali velike množice, ki ležijo na črti ali krogu, včasih s tremi ali štirimi dodatnimi točkami, ki so izven glavnega vlečenja. (Ni nujno, da imajo same točke cele koordinate — vprašanje je o razdaljah med njimi.)

Nihče ni prišel do velikega niza točk s katero koli drugo konfiguracijo, vendar nihče ni dokazal, da so druge konfiguracije nemogoče. V skoraj 80 letih od rezultatov Anninga in Erdősa predmet ni videl skoraj nobenega napredka - vse do zdaj.

Greenfeld, Iliopoulou in Peluse so dokazano da morajo vse točke v velikem nizu celoštevilskih razdalj - razen morda redke peščice izstopajočih točk - ležati na eni premici ali krogu. "Če želite imeti velik niz, kjer so vse razdalje v parih cela števila, potem so krogi in črte edini igralci," je rekel József Solymosi Univerze Britanske Kolumbije. Njihov rezultat je označil za "fantastično rešitev".

Novi pristop uporablja ideje in tehnike s treh različnih področij matematike: kombinatorike, teorije števil in algebraične geometrije. To združevanje različnih področij bi lahko pomenilo pravi psihološki preboj, je rekel Terence tao, matematik na Kalifornijski univerzi v Los Angelesu.

Alex Iosevič, z Univerze v Rochestru, se strinja. "Postavili so zelo trdne temelje za zelo širok nabor problemov," je dejal. "V mojih mislih ni nobenega dvoma, da bo to našlo še globlje aplikacije."

Meje preprostosti

Znotraj ravnine je enostavno izbrati neskončno množico točk, ki so med seboj oddaljene celo število — preprosto vzemite svojo najljubšo črto, si zamislite številsko črto, ki je na njej, in uporabite nekatere ali vse točke, ki ustrezajo celim številom. Toda to je edini način za konstruiranje neskončne cele razdalje v ravnini, kot sta ugotovila Anning in Erdős leta 1945. Takoj, ko imate samo tri točke, ki niso vse na isti premici, postane vaša konfiguracija tako omejena, da je nemogoče dodati neskončno veliko več točk.

Razlog se skriva v preprosti geometriji. Predstavljajte si, da začnete z dvema točkama, A in B, ki sta med seboj oddaljeni celo število. Če želite dodati tretjo točko, C, ki je celo število oddaljena od A in B, vendar ne leži na premici skozi njiju, večina točk v ravnini ne bo delovala. Edine možne točke živijo na posebnih krivuljah, imenovanih hiperbole, ki sekajo med A in B. Če sta A in B na primer 4 enote narazen, potem obstajajo natanko štiri te hiperbole. (Hiperbola ima običajno dva različna dela, tako da na primer dve rdeči krivulji na spodnji sliki tvorita eno hiperbolo.)

Ko izberete C (ki je v tem primeru 3 enote od A in 5 enot od B), nimate več možnosti za dodajanje več točk. Vsaka točka, ki jo lahko dodate, mora ležati na eni od hiperbol med A in B ali na premici, ki teče skozi njiju. Ležati pa mora tudi na eni od hiperbol med A in C ter eni od hiperbol med B in C (ali ustreznima črtama) - z drugimi besedami, novo točko je mogoče postaviti samo tam, kjer se sekajo tri hiperbole ali črte (čeprav ne bo delovalo vsako presečišče). Teh hiperbol in premic je na začetku le končno veliko in dve hiperboli (ali premici) se lahko sekata v največ štirih točkah. Torej imate na koncu le končno veliko presečišč, med katerimi lahko izbirate - ne morete zgraditi neskončnega niza.

Ko pride do razumevanja, kako dejansko izgleda končni niz celih oddaljenih točk, pristop hiperbole hitro postane okoren. Ko dodajate točke, se morate spopasti z naraščajočim številom hiperbol. Na primer, do takrat, ko bo imel vaš niz le 10 točk, boste z dodajanjem 11. ustvarili 10 novih družin hiperbol – vse tiste med vašo novo točko in vsako od točk, ki so že v nizu. "Ne morete dodati veliko točk, ker se boste izgubili v vseh teh hiperbolah in križiščih," je dejal Greenfeld.

Zato so matematiki iskali bolj obvladljiva načela za konstruiranje velikih nizov celih oddaljenih točk, ki ne ležijo na premici. Vendar so se lahko domislili samo enega pristopa: postavite svoje točke na krog. Če želite celoštevilsko razdaljo, na primer z bilijonom točk, obstajajo načini, da pridete do bilijona točk na krogu s polmerom 1, katerih medsebojne razdalje so ulomki. Nato lahko napihnete krog, dokler se vse delne razdalje ne spremenijo v cela števila. Več točk kot želite v svojem kompletu, več jih boste potrebovali za napihovanje kroga.

Z leti so matematiki prišli le do nekoliko bolj eksotičnih primerov. Znajo sestaviti velike celoštevilske množice razdalj, v katerih vse točke razen štirih ležijo na premici ali vse razen treh ležijo na krogu. Mnogi matematiki sumijo, da so to edini veliki nizi celoštevilskih razdalj, v katerih niso vse točke na premici ali krogu. To bodo zagotovo vedeli, če bodo lahko kdaj dokazali nekaj, kar se imenuje Bombieri-Langova domneva. Toda matematiki so razdeljeni glede tega, ali je ta domneva verjetno resnična.

Od dela Anninga in Erdősa leta 1945 so matematiki le malo napredovali pri razumevanju nizov celoštevilskih razdalj. Sčasoma se je zdelo, da se je težava s celoštevilsko razdaljo pridružila vrsti drugih težav v kombinatoriki, teoriji števil in geometriji, ki jih je preprosto navesti, vendar se jih zdi nemogoče rešiti. "To je merilo, kako patetična je naša matematika," je dejal Tao.

Na nek način je bil problem cele razdalje žrtev svojih zgodnjih uspehov. Dokaz hiperbole je s svojo genialno preprostostjo simbol filozofije, ki jo je zagovarjal Erdős, zelo vpliven matematik, ki je pogosto govoril o "Knjigi" - namišljenem obsegu najelegantnejših dokazov v matematiki. Kultura preprostosti, ki jo je spodbujal Erdős, je privedla do "ogromnih rezultatov" v kombinatorični geometriji, je dejal Iosevich. Lahko pa vodi tudi do slepih peg - v tem primeru o vrednosti vnašanja pristopov iz algebraične geometrije.

"Mislim, da ne boste našli rezultata [v algebrski geometriji], dokazanega v zadnjih 50 letih, ki ni zelo tehnično vpleten in neurejen," je dejal Iosevich. "Včasih pa morajo biti stvari takšne."

V retrospektivi je problem cele razdalje čakal na matematike, ki so bili pripravljeni razmisliti o bolj neukrotljivih krivuljah kot hiperbolah in nato uporabiti rekonditna orodja iz algebraične geometrije in teorije števil, da bi jih ukrotili. "Potrebovali so ljudi z zadostno širino znanja in zanimanja," je dejal Iosevič.

Večina matematikov, je dejal, je zadovoljna z uporabo nekaj orodij v enem kotu matematike v svoji celotni karieri. Toda Greenfeld, Iliopoulou in Peluse so neustrašni raziskovalci, je dejal Iosevich. "Na matematiko gledajo kot na koherentno celoto."

Kompleksiranje problema

Poleti 2021 se je Greenfeldova odločila, da je čas, da se loti problema harmonične analize, o katerem je razmišljala že od podiplomskega študija. Klasična harmonična analiza, ki je osnova za obdelavo signalov v resničnem svetu, se nanaša na razgradnjo signalov na sinusne valove različnih frekvenc in faz. Ta postopek deluje, ker je mogoče sestaviti neskončen seznam sinusnih valov, ki v kombinaciji zajamejo vse značilnosti katerega koli signala brez kakršne koli redundance.

Pogosto pa želijo raziskovalci preučiti nekaj bolj zapletenega kot enodimenzionalni signal. Na primer, morda bodo želeli razstaviti signal na disku v letalu. Toda disk lahko gosti samo omejeno zbirko združljivih sinusnih valov - premalo, da bi zajeli vedenje vseh možnih signalov na disku. Nato se pojavi vprašanje: kako velika je lahko ta končna zbirka?

V taki zbirki lahko frekvence sinusov predstavimo kot točke na ravnini, ki se zdijo nenaklonjene združevanju v črte in kroge: nikoli ne boste našli treh točk, ki so vse blizu iste črte, ali štirih, ki so vse blizu v isti krog. Greenfeld je upal, da bo s tem odporom dokazal, da lahko ti nizi frekvenc vsebujejo le nekaj točk.

Na srečanju leta 2021 na Univerzi v Bonnu se je Greenfeld udeležil pogovora o »metodi determinant«, tehniki iz teorije števil, ki se lahko uporabi za oceno, koliko celih točk določenega tipa lahko leži na krivuljah. Spoznala je, da je to orodje morda prav tisto, kar potrebuje. Greenfeld je zaposlil Iliopoulouja in Peluseja, ki sta bila tudi na sestanku. "Skupaj sva se začela učiti te metode," je dejal Greenfeld.

Toda kljub številnim prizadevanjem se zdi, da metode determinante niso mogli prilagoditi svojemu namenu in do pomladi 2023 so se počutili malodušne. Iosevič je povabil Greenfelda in Peluseja, naj se odpeljeta na obisk v Rochester. "Zato smo razmišljali, 'V redu, šli bomo v Rochester in pogovor z Alexom nas bo ponovno poživil,'" je dejal Peluse. A kot se je izkazalo, so pristali v Rochesterju že okrepčani, zahvaljujoč okrepljeni razpravi o nizih celoštevilskih razdalj na njihovem nenačrtovanem obvozu ob reki Susquehanna v Pensilvaniji.

Na načrtovano večerjo z Iosevičem so prispeli prepozno, vendar so ga našli čakati v hotelskem preddverju z vrečkami hrane za s seboj. Odpustil jim je zamudo - in naslednje jutro, ko so mu povedali o svojem načrtu za reševanje naborov celoštevilskih razdalj, je bil več kot prizanesljiv. "Bil je tako navdušen," se je spominjala Peluse. "Čustveno je bil to velik zagon."

Kot pri pristopu hiperbole so Greenfeld, Iliopoulou in Peluse poskušali nadzorovati strukturo nizov celoštevilskih razdalj z identifikacijo družin krivulj, na katerih morajo ležati točke. Metoda hiperbole začne postajati preveč zapletena, takoj ko imate več kot nekaj točk, vendar so Greenfeld, Iliopoulou in Peluse ugotovili, kako upoštevati več točk hkrati, tako da celotno konfiguracijo premaknejo v prostor z višjo dimenzijo.

Da bi videli, kako to deluje, predpostavimo, da začnete z "referenčno" točko A v nizu celih razdalj. Vsaka druga točka v nizu je celoštevilska razdalja od A. Točke živijo v ravnini, vendar lahko ravnino premaknete v tridimenzionalni prostor tako, da vsaki točki prilepite tretjo koordinato, katere vrednost je razdalja od A. Na primer , predpostavimo, da je A točka (1, 3). Nato se točka (4, 7), ki je 5 enot oddaljena od A, v tridimenzionalnem prostoru spremeni v točko (4, 7, 5). Ta postopek pretvori ravnino v stožec v tridimenzionalnem prostoru, katerega konica je na A, zdaj označena (1, 3, 0). Celoštevilske oddaljene točke postanejo točke v tridimenzionalnem prostoru, ki ležijo na stožcu in tudi na določeni mreži.

Podobno, če izberete dve referenčni točki, A in B, lahko pretvorite točke na ravnini v točke v štiridimenzionalnem prostoru - vsaki točki samo dajte dve novi koordinati, katerih vrednosti sta njeni razdalji do A in B. Ta postopek pretvori ravnino v ukrivljeno površino v štiridimenzionalnem prostoru. Na ta način lahko še naprej dodajate več referenčnih točk. Z vsako novo referenčno točko se dimenzija poveča za eno in ravnina se preslika na še bolj razgibano površino (ali, kot pravijo matematiki, površino višje stopnje).

S tem okvirom so raziskovalci uporabili determinantno metodo iz teorije števil. Determinante so števila, običajno povezana z matricami, ki zajemajo množico geometrijskih lastnosti zbirke točk - na primer, določena determinanta lahko meri površino trikotnika, ki ga tvorijo tri točke. Metoda determinante ponuja način za uporabo takšnih determinant za oceno števila točk, ki hkrati ležijo na gibljivi površini in na rešetki - prav takšna situacija, s katero so se ukvarjali Greenfeld, Iliopoulou in Peluse.

Raziskovalci so uporabili linijo dela, ki je temeljila na metodi determinante, da bi pokazali, da morajo vse točke ležati na majhnem številu posebnih krivulj, ko svojo nastavljeno celoštevilsko razdaljo premaknejo na ustrezno visoko dimenzijo. Te krivulje, kadar njihove sence v ravnini niso črta ali krog, ne morejo vsebovati veliko mrežnih točk, ki so edini kandidati za točke v naboru celoštevilskih razdalj. To pomeni, da je število točk v nizu, ki lahko ležijo zunaj glavne črte ali kroga, omejeno - raziskovalci so pokazali, da mora biti manjše od zelo počasi rastoče funkcije premera niza.

Njihova meja ne dosega standarda domneve o "štirih točkah od premice ali treh točkah od kroga", za katero mnogi matematiki verjamejo, da velja za velike nize celih razdalj. Kljub temu rezultat kaže, da je "bistvo domneve resnično," je dejal Jacob Fox z univerze Stanford. Popoln dokaz domneve bo verjetno zahteval še eno infuzijo novih idej, pravijo matematiki.

Visokodimenzionalna shema kodiranja ekipe je "izjemno robustna," je dejal Iosevich. "Načeloma ne obstajajo samo aplikacije - obstajajo aplikacije, o katerih že razmišljam."

Greenfeld, Iliopoulou in Peluse upajo, da bo ena aplikacija namenjena njihovemu izvirnemu problemu harmonične analize, h kateremu se zdaj vračajo. Njihov rezultat na nizih celih razdalj "bi lahko bil odskočna deska k temu," je dejal Greenfeld.

Sinteza kombinatorike z algebrsko geometrijo, ki so jo začeli raziskovalci, se ne bo ustavila pri nizih celih razdalj ali sorodnih problemih v harmonični analizi, je napovedal Iosevich. "Verjamem, da je to, kar vidimo, konceptualni preboj," je dejal. "To pošilja sporočilo ljudem na obeh področjih, da je to zelo produktivna interakcija."

Pošilja tudi sporočilo o vrednosti včasih zapletanja težave, je dejal Tao. Matematiki si običajno prizadevajo za obratno, je opozoril. "Toda to je primer, ko je zapletenost problema pravzaprav prava poteza."

Napredek je spremenil način razmišljanja o krivuljah z visoko stopnjo, je dejal. "Včasih so lahko tvoji prijatelji in ne sovražniki."