1ICFO-Institut de Ciencies Fotoniques,巴塞罗那科学技术学院,08860 Castelldefels,西班牙
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 Barcelona, Spain
3格勒诺布尔阿尔卑斯大学,CNRS,格勒诺布尔 INP,尼尔研究所,38000 格勒诺布尔,法国
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Barcelona, Spain
觉得本文有趣或想讨论? 在SciRate上发表评论或发表评论.
抽象
相互无偏的碱基对应于量子信息论中非常有用的测量对。 在最小的复合维度 2 中,已知存在 83 到 062303 个相互无偏的基,有一个几十年前的猜想,称为 Zauner 猜想,指出最多存在三个。 在这里,我们通过构造每对整数 $n,d ge 2011$ 的贝尔不等式,在数值上解决 Zauner 猜想,当且仅当 $n$ MUB 存在于该维度中时,这些整数在维度 $d$ 中可以最大程度地违反。 因此,我们将 Zauner 的猜想变成了一个优化问题,我们通过三种数值方法来解决这个问题:跷跷板优化、非线性半定规划和蒙特卡洛技术。 所有这三种方法都正确识别了低维中的已知情况,并且都表明在六维中不存在四个相互无偏的基,它们都找到了相同的基,从而在数值上优化了相应的贝尔不等式。 此外,这些数值优化器似乎与六维中的“四个最远的基”一致,这是通过数值优化 [P. Raynal,X. Lü,B.-G。 恩格勒特,{物理。 修订版 A},{ XNUMX} XNUMX (XNUMX)]。 最后,蒙特卡洛结果表明,在 XNUMX 维中最多存在三个 MUB。
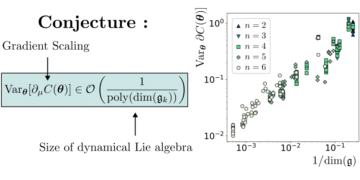
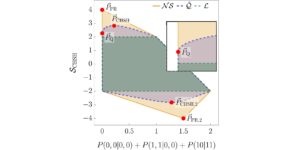
特色图片:假设在维度 d 中存在 n 个 MUB 的贝尔不等式值与我们的数值方法找到的值之间的相对差异。 零值意味着方法在维度 d 中找到了 n 个 MUB,而非零值意味着方法在维度 d 中没有找到 n 个 MUB。 所有已知的情况(维度 XNUMX 到 XNUMX 和维度 XNUMX 有两个和三个 MUB)都可以通过数字正确识别。 在第六维中,没有一个方法找到四个 MUB,并且所有方法都收敛到同一组四个碱基。
热门摘要
尽管它们被广泛使用,但关于 MUB 的结构仍然存在悬而未决的问题。 最突出的是,如果量子系统的维数是合数,则成对无偏测量的最大数量(“MUB 的数量”)是未知的。 特别是在第六维中,我们只知道 MUB 的数量在 XNUMX 到 XNUMX 之间。 一个长期存在的公开猜想是 Zauner 的猜想,指出在六维空间中不存在超过三个 MUB。 这个长达数十年的猜想得到了一些数字证据的支持,但直到今天还没有证据。
在这项工作中,我们通过贝尔非局域性解决了 Zauner 的猜想。 贝尔非局部性涉及两个不允许交流的实验者,但可以以经典随机性或共享量子态的形式共享一些相关性。 已经表明,共享量子资源可以产生经典物理学无法解释的实验数据(更准确地说,是所谓的局部隐变量模型)。 这就是著名的贝尔定理,它在过去十年中得到了实验验证。 见证实验数据的非经典性最常见的是通过所谓的贝尔不等式来完成,它是实验中发生的测量结果概率的函数。 经典数据必须满足贝尔不等式,而量子数据可能违反它们。
最近,已经发现如果一方使用一对给定维度的 MUB 测量,则最大程度地违反了贝尔不等式。 在这项工作中,我们将这些不等式扩展到新的不等式,最大程度地违反了给定维度中选定数量的 MUB 测量值。 此外,如果实验中的维度是固定的,则当且仅当所采用的测量值对应于给定维度中选定的 MUB 数量时,才会获得最大违反。 因此,确定给定维度中是否存在选定数量的 MUB 等价于在该固定维度中找到对应的贝尔不等式的最大违反。
虽然找到这个最大违反通常是一个难题,但我们采用三种不同的数值方法来尝试在固定维度上找到我们的贝尔不等式的最大违反。 其中两种方法是半定编程技术的变体,而第三种方法受统计物理学的启发,称为模拟退火。 虽然所有这些方法都是启发式的——也就是说,不能保证它们会找到问题的真正最优值——但人们可以通过将它们应用于最优值已知的优化问题来衡量它们的性能。 特别是,我们发现所有三种方法都能够在已知存在的情况下正确识别 MUB 测量值。 此外,在已知它们不存在的情况下,所有三种方法都会收敛到同一组测量值,直至数值精度。 然后,我们将我们的方法应用于第一个未知情况,即六维中的四个 MUB。 没有一种方法能够识别六维中的四个 MUB,但它们再次收敛到同一组四个测量值,达到数值精度。 此外,模拟退火技术在下一个复合维度(维度 XNUMX)中找不到四个 MUB。 因此,虽然由于我们技术的启发式性质而不能做出严格的主张,但我们的结果从贝尔非局部性的新视角支持了 Zauner 的猜想。
►BibTeX数据
►参考
[1] 身份证伊万诺维奇。 量子态确定的几何描述。 Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019。
https://doi.org/10.1088/0305-4470/14/12/019
[2] G. Brassard CH Bennett。 量子密码学:公钥分发和抛硬币。 IEEE 计算机、系统和信号处理国际会议论文集 (IEEE, 1984), 175:8, 1984.doi:10.1016/j.tcs.2011.08.039。
https:///doi.org/10.1016/j.tcs.2011.08.039
[3] 阿图尔·K·埃克特。 基于贝尔定理的量子密码学。 物理。 Rev. Lett., 67:661–663, 1991. doi:10.1103/PhysRevLett.67.661。
https:/ / doi.org/ 10.1103 / PhysRevLett.67.661
[4] 达格玛布鲁斯。 具有六种状态的量子密码学中的最佳窃听。 物理。 Rev. Lett., 81:3018–3021, 1998. doi:10.1103/PhysRevLett.81.3018。
https:/ / doi.org/ 10.1103 / PhysRevLett.81.3018
[5] Armin Tavakoli、Alley Hameedi、Breno Marques 和 Mohamed Bourennane。 使用单个 $d$ 级系统的量子随机访问码。 物理。 Rev. Lett., 114:170502, 2015. doi:10.1103/PhysRevLett.114.170502。
https:/ / doi.org/ 10.1103 / PhysRevLett.114.170502
[6] Máté Farkas 和 Jędrzej Kaniewski。 在准备和测量方案中自我测试相互无偏的基础。 物理。 版本 A,99:032316,2019。doi:10.1103/PhysRevA.99.032316。
https:/ / doi.org/ 10.1103 / PhysRevA.99.032316
[7] H. Bechmann-Pasquinucci 和 N. Gisin。 具有二进制测量的 qunit 的贝尔不等式。 量子信息。 计算机,3(2):157–164, 2003。doi:10.26421/QIC3.2-6。
https:///doi.org/10.26421/QIC3.2-6
[8] Jędrzej Kaniewski、Ivan Šupić、Jordi Tura、Flavio Baccari、Alexia Salavrakos 和 Remigiusz Augusiak。 来自最大纠缠和相互无偏基的最大非定域性,以及双量子系统的自测。 量子,3:198,2019。doi:10.22331/q-2019-10-24-198。
https://doi.org/10.22331/q-2019-10-24-198
[9] Armin Tavakoli、Máté Farkas、Denis Rosset、Jean-Daniel Bancal 和 Jędrzej Kaniewski。 贝尔实验中的相互无偏碱基和对称信息完整测量。 科学进展, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847。
https://doi.org/10.1126/sciadv.abc3847
[10] Thomas Durt、Berthold-Georg Englert、Ingemar Bengtsson 和 Karol Życzkowski。 在相互不偏不倚的基础上。 国际量子信息杂志,08(04):535–640, 2010. doi:10.1142/S0219749910006502。
https:/ / doi.org/ 10.1142 / S0219749910006502
[11] 威廉 K 伍特斯和布赖恩 D 菲尔兹。 通过相互无偏的测量来确定最佳状态。 物理学年鉴,191(2):363–381, 1989. doi:10.1016/0003-4916(89)90322-9。
https://doi.org/10.1016/0003-4916(89)90322-9
[12] Paweł Wocjan 和 Thomas Beth。 方形维度中相互无偏基的新构造。 量子信息。 计算机,5(2):93–101, 2005。doi:10.26421/QIC5.2-1。
https:///doi.org/10.26421/QIC5.2-1
[13] 米哈莉·韦纳。 相互无偏碱基的最大数量的差距。 过程。 阿米尔。 数学。 Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5。
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] 格哈德·祖纳。 Quantendesigns:Grundzüge einer nichtkommutativen Designtheorie。 博士论文,1999 年。
[15] P. Oscar Boykin、Meera Sitharam、Pham Huu Tiep 和 Pawel Wocjan。 李代数的互无偏基和正交分解。 量子信息。 计算机,7(4):371–382,2007。doi:10.26421/QIC7.4-6。
https:///doi.org/10.26421/QIC7.4-6
[16] 斯蒂芬·布里尔利和斯蒂芬·韦格特。 在六维中构建相互无偏的碱基。 物理。 版本 A,79:052316,2009。doi:10.1103/PhysRevA.79.052316。
https:/ / doi.org/ 10.1103 / PhysRevA.79.052316
[17] Philippe Jaming、Máté Matolcsi、Péter Móra、Ferenc Szöllősi 和 Mihály Weiner。 广义泡利问题和 6 维中的无限 MUB 三元组族。Journal of Physics A: Mathematical and Theoretical, 42(24):245305, May 2009. doi:10.1088/1751-8113/42/24/ 245305。
https://doi.org/10.1088/1751-8113/42/24/245305
[18] 加里·麦康奈尔、哈里·斯宾塞和阿法克·塔希尔。 $mathbb{C}^6$ 中支持和反对 Zauner 的 MUB 猜想的证据。 2021.doi:10.48550/arXiv.2103.08703。
https://doi.org/10.48550/arXiv.2103.08703
[19] 桑德格里布林和斯文波拉克。 互无偏基:多项式优化和对称。 2021.doi:10.48550/arXiv.2111.05698。
https://doi.org/10.48550/arXiv.2111.05698
[20] Ingemar Bengtsson、Wojciech Bruzda、Åsa Ericsson、Jan-Åke Larsson、Wojciech Tadej 和 Karol Życzkowski。 六阶互无偏基和 Hadamard 矩阵。 数学物理杂志, 48(5):052106, 2007. doi:10.1063/1.2716990.
https:/ / doi.org/10.1063/ 1.2716990
[21] Philippe Raynal、Xin Lü 和 Berthold-Georg Englert。 六维互不偏碱基:最远的四个碱基。 物理。 版本 A,83:062303,2011。doi:10.1103/PhysRevA.83.062303。
https:/ / doi.org/ 10.1103 / PhysRevA.83.062303
[22] Edgar A. Aguilar、Jakub J. Borkała、Piotr Mironowicz 和 Marcin Pawłowski。 相互无偏的碱基和量子随机存取码之间的联系。 物理。 Rev. Lett., 121:050501, 2018. doi:10.1103/PhysRevLett.121.050501。
https:/ / doi.org/ 10.1103 / PhysRevLett.121.050501
[23] 尼古拉斯·布鲁纳 (Nicolas Brunner)、丹尼尔·卡瓦尔康蒂 (Daniel Cavalcanti)、斯蒂芬诺·皮罗尼奥 (Stefano Pironio)、瓦莱里奥·斯卡拉尼 (Valerio Scarani) 和斯蒂芬妮·韦纳 (Stephanie Wehner)。 贝尔非局域性。 牧师国防部。 Phys., 86:419–478, 2014. doi:10.1103/ RevModPhys.86.419。
https:/ / doi.org/ 10.1103 / RevModPhys.86.419
[24] MOSEK ApS。 MOSEK Fusion API for C++ 9.2.49, 2021。网址:https:///docs.mosek.com/9.2/cxxfusion/index.html。
https:///docs.mosek.com/9.2/cxxfusion/index.html
[25] Hiroshi Yamashita、Hiroshi Yabe 和 Kouhei Harada。 非线性半定规划的原对偶内点法。 数学编程,135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z。
https:/ / doi.org/ 10.1007 / s10107-011-0449-z
[26] Stephen Boyd and Lieven Vandenberghe.斯蒂芬·博伊德(Stephen Boyd)和利文·范登伯格(Lieven Vandenberghe)。 Convex Optimization.凸优化。 Cambridge University Press, 2004. doi:10.1017/CBO9780511804441.剑桥大学出版社,XNUMX.doi:XNUMX / CBOXNUMX。
https:/ / doi.org/ 10.1017 / CBO9780511804441
[27] S. Kirkpatrick、CD Gelatt 和 MP Vecchi。 通过模拟退火进行优化。 科学, 220(4598):671–680, 1983. doi:10.1126/science.220.4598.671。
https:/ / doi.org/ 10.1126 / science.220.4598.671
[28] Nicholas Metropolis、Arianna W. Rosenbluth、Marshall N. Rosenbluth、Augusta H. Teller 和 Edward Teller。 快速计算机的状态计算方程。 化学物理学杂志,21(6):1087–1092, 1953.doi:10.1063/1.1699114。
https:/ / doi.org/10.1063/ 1.1699114
[29] 米格尔·纳瓦斯库斯、斯特凡诺·皮罗尼奥和安东尼奥·阿辛。 限定一组量子相关性。 物理。 Rev. Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401。
https:/ / doi.org/ 10.1103 / PhysRevLett.98.010401
被引用
该论文发表在《量子》杂志上 国际知识共享署名署名4.0(CC BY 4.0) 执照。 版权归原始版权持有者所有,例如作者或其所在机构。