1850 সালে টমাস পেনিংটন কার্কম্যান, একজন গণিতবিদ যখন তিনি চার্চ অফ ইংল্যান্ডে একজন ভিকার হিসাবে তার প্রধান দায়িত্ব পালন করছিলেন না, তখন তার "স্কুলগার্ল সমস্যা" বর্ণনা করেছিলেন: "একটি স্কুলে পনের জন তরুণী পরপর সাত দিন ধরে তিনবার হাঁটতে বের হয়: এটির ব্যবস্থা করা প্রয়োজন। তাদের প্রতিদিন, যাতে কেউ দু'বার সমানে হাঁটতে না পারে।"
একজন আধুনিক গণিতবিদদের কাছে, এই ধরনের সমস্যাটিকে হাইপারগ্রাফ হিসাবে কল্পনা করা হয় - তিন বা তার বেশি গোষ্ঠীতে সংগৃহীত নোডের একটি সেট। 15টি স্কুল ছাত্রী হল নোড, এবং "তিনটি সমতল" এর প্রতিটি দলকে একটি ত্রিভুজ হিসাবে ভাবা যেতে পারে, তিনটি লাইন, বা প্রান্ত, তিনটি নোডকে সংযুক্ত করে।
কার্কম্যানের সমস্যাটি মূলত জিজ্ঞাসা করে যে এই ত্রিভুজগুলির এমন একটি ব্যবস্থা আছে যা সমস্ত স্কুলছাত্রীকে একে অপরের সাথে সংযুক্ত করে, তবে অতিরিক্ত সীমাবদ্ধতার সাথে যে দুটি ত্রিভুজ একটি প্রান্ত ভাগ করে না। এজ-শেয়ারিং বোঝাবে যে দুই স্কুল ছাত্রীকে একাধিকবার একসাথে হাঁটতে হবে। এই নিষেধাজ্ঞার অর্থ হল প্রতিটি মেয়ে এক সপ্তাহের জন্য প্রতিদিন দুটি নতুন বন্ধুর সাথে হাঁটবে, যাতে প্রতিটি সম্ভাব্য জুটি ঠিক একবার একসাথে হয়।
এই সমস্যাটি এবং এর মতো অন্যান্য বিষয়গুলি প্রায় দুই শতাব্দী ধরে গণিতবিদদের বিভ্রান্ত করে রেখেছে যখন থেকে কার্কম্যান তার প্রশ্ন উত্থাপন করেছেন। 1973 সালে, কিংবদন্তি গণিতবিদ পল এরডস অনুরূপ একটি জাহির করেছিলেন। তিনি জিজ্ঞাসা করেছিলেন যে দুটি আপাতদৃষ্টিতে বেমানান বৈশিষ্ট্য সহ একটি হাইপারগ্রাফ তৈরি করা সম্ভব কিনা। প্রথমত, নোডের প্রতিটি জোড়া অবশ্যই একটি ত্রিভুজ দ্বারা সংযুক্ত থাকতে হবে, যেমন স্কুলের ছাত্রীদের সাথে। এই বৈশিষ্ট্যটি ত্রিভুজ সহ গ্রাফটিকে ঘন করে তোলে। দ্বিতীয় প্রয়োজনীয়তা ত্রিভুজগুলিকে খুব সুনির্দিষ্ট উপায়ে ছড়িয়ে দিতে বাধ্য করে। (বিশেষত, এটির জন্য প্রয়োজন যে ত্রিভুজগুলির যে কোনও ছোট গোষ্ঠীর জন্য, ত্রিভুজগুলির চেয়ে কমপক্ষে তিনটি বেশি নোড রয়েছে।) "আপনার এই সামান্য বিপরীত আচরণ রয়েছে যেখানে আপনার কাছে একটি ঘন সামগ্রিক বস্তু রয়েছে যার কোনও ঘন অংশ নেই," বলেছেন ডেভিড কনলন, ক্যালিফোর্নিয়া ইনস্টিটিউট অফ টেকনোলজির একজন গণিতবিদ।
এই জানুয়ারি, মধ্যে একটি জটিল 50-পৃষ্ঠার প্রমাণ, চারজন গণিতবিদ প্রমাণ করেছেন যে আপনার কাছে পর্যাপ্ত নোড থাকলে এমন হাইপারগ্রাফ তৈরি করা সবসময় সম্ভব। "[তারা] যে পরিমাণ কারিগরিতার মধ্য দিয়ে গেছে, কেবল এটি পাওয়ার জন্য, এটি আশ্চর্যজনক ছিল," বলেছেন অ্যালান লো, বার্মিংহাম বিশ্ববিদ্যালয়ের একজন গণিতবিদ। কনলন একমত: "এটি সত্যিই একটি চিত্তাকর্ষক কাজ।"
গবেষণা দলটি এমন একটি সিস্টেম তৈরি করেছে যা ত্রিভুজ বেছে নেওয়ার জন্য একটি এলোমেলো প্রক্রিয়া শুরু করে এবং তাদের প্রয়োজন অনুসারে অত্যন্ত যত্ন সহকারে এটিকে প্রকৌশলী করার মাধ্যমে এরডসের শয়তানী প্রয়োজনীয়তাগুলিকে সন্তুষ্ট করেছিল। "প্রমাণে যাওয়া কঠিন পরিবর্তনের সংখ্যা আসলে বিস্ময়কর রকমের," কনলন বলেছেন।
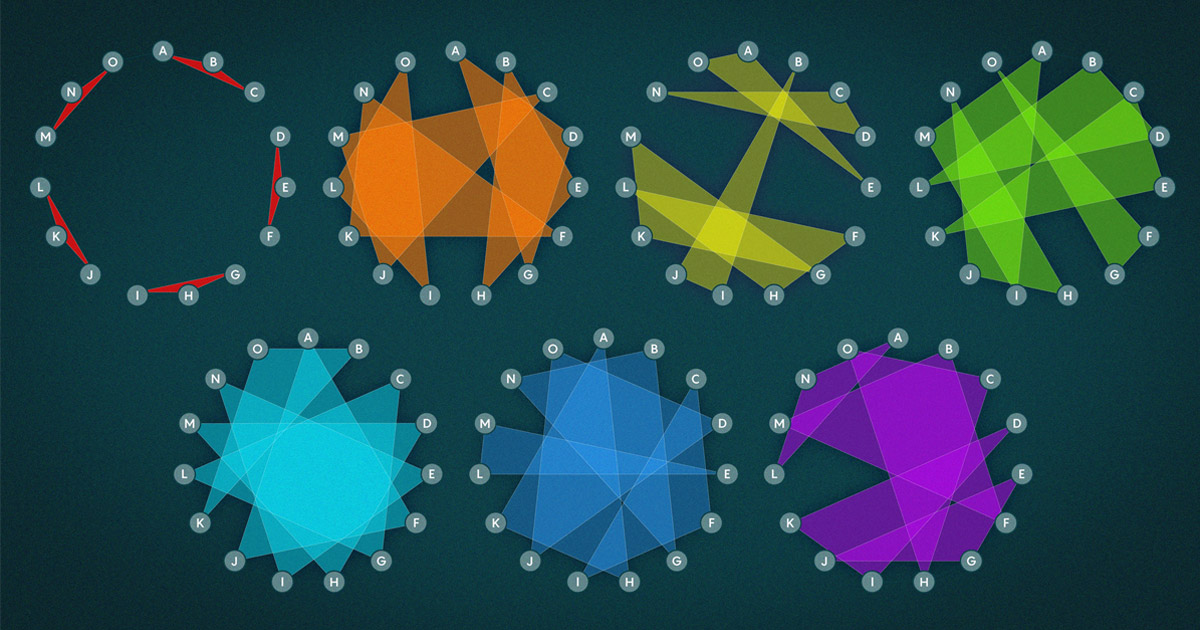
তাদের কৌশলটি ছিল স্বতন্ত্র ত্রিভুজ থেকে সাবধানে হাইপারগ্রাফ তৈরি করা। উদাহরণস্বরূপ, আমাদের 15 জন স্কুল ছাত্রীকে কল্পনা করুন। প্রতিটি জোড়ার মধ্যে একটি রেখা আঁকুন।
এখানে লক্ষ্য হল এই রেখাগুলির উপরে ত্রিভুজগুলি চিহ্নিত করা যাতে ত্রিভুজ দুটি প্রয়োজনীয়তা পূরণ করে: প্রথমত, কোন দুটি ত্রিভুজ একটি প্রান্ত ভাগ করে না। (এই প্রয়োজনীয়তা পূরণকারী সিস্টেমগুলিকে স্টেইনার ট্রিপল সিস্টেম বলা হয়।) এবং দ্বিতীয়ত, নিশ্চিত করুন যে ত্রিভুজের প্রতিটি ছোট উপসেট যথেষ্ট পরিমাণে নোড ব্যবহার করে।
গবেষকরা যেভাবে এটি করেছিলেন তা সম্ভবত একটি উপমা দিয়ে সবচেয়ে ভাল বোঝা যায়।
বলুন যে প্রান্ত থেকে ত্রিভুজ তৈরি করার পরিবর্তে, আপনি লেগো ইট দিয়ে ঘর তৈরি করছেন। আপনার তৈরি করা প্রথম কয়েকটি ভবন অসামান্য, কাঠামোগত শক্তিবৃদ্ধি এবং বিস্তৃত অলঙ্করণ সহ। একবার আপনি এগুলি সম্পন্ন করার পরে, সেগুলিকে একপাশে রাখুন। তারা একটি "শোষক" হিসাবে পরিবেশন করবে - এক ধরনের কাঠামোগত মজুদ।
এখন আপনার অবশিষ্ট ইট দিয়ে বিল্ডিং তৈরি করা শুরু করুন, অনেক পরিকল্পনা ছাড়াই এগিয়ে যান। যখন আপনার লেগোসের সরবরাহ কমে যায়, তখন আপনি নিজেকে কিছু বিপথগামী ইট বা কাঠামোগতভাবে অস্বাস্থ্যকর বাড়ি খুঁজে পেতে পারেন। কিন্তু যেহেতু শোষক বিল্ডিংগুলি খুব বেশি এবং শক্তিশালী, আপনি এখানে এবং সেখানে কিছু ইট ছিঁড়ে ফেলতে পারেন এবং বিপর্যয় না ঘটিয়ে ব্যবহার করতে পারেন।
স্টেইনার ট্রিপল সিস্টেমের ক্ষেত্রে, আপনি ত্রিভুজ তৈরি করার চেষ্টা করছেন। আপনার শোষক, এই ক্ষেত্রে, প্রান্তের একটি সাবধানে নির্বাচিত সংগ্রহ। আপনি যদি সিস্টেমের বাকি অংশগুলিকে ত্রিভুজগুলিতে সাজাতে অক্ষম হন তবে আপনি কিছু প্রান্ত ব্যবহার করতে পারেন যা শোষকের দিকে নিয়ে যায়। তারপর, যখন আপনি এটি করছেন, আপনি ত্রিভুজ মধ্যে শোষক নিজেই ভেঙ্গে.
শোষণ সবসময় কাজ করে না। কিন্তু গণিতবিদরা এই প্রক্রিয়ার সাথে টিঙ্কার করেছেন, বাধাগুলিকে ঘিরে নতুন উপায় খুঁজে পেয়েছেন। উদাহরণস্বরূপ, পুনরাবৃত্ত শোষণ নামক একটি শক্তিশালী বৈকল্পিক প্রান্তগুলিকে সেটের একটি নেস্টেড সিকোয়েন্সে বিভক্ত করে, যাতে প্রতিটি পরবর্তী বৃহত্তমটির জন্য একটি শোষক হিসাবে কাজ করে।
"গত দশকে বা তারও বেশি সময় ধরে ব্যাপক উন্নতি হয়েছে," কনলন বলেছেন। "এটি একটি শিল্প ফর্মের কিছু, কিন্তু তারা সত্যিই এটিকে এই সময়ে উচ্চ শিল্পের স্তরে নিয়ে গেছে।"
এমনকি পুনরাবৃত্তিমূলক শোষণের সাথেও এরডসের সমস্যাটি জটিল ছিল। "এটি খুব দ্রুত পরিষ্কার হয়ে গেছে কেন এই সমস্যাটি সমাধান করা হয়নি," বলেছেন মেহতাব সাহনি, চার গবেষকদের একজন যারা এটি সমাধান করেছেন, সাথে অশ্বিন সাহ, যিনি সাহনির সাথে ম্যাসাচুসেটস ইনস্টিটিউট অফ টেকনোলজিতে স্নাতক ছাত্র; মাইকেল সিমকিন, হার্ভার্ড বিশ্ববিদ্যালয়ের গাণিতিক বিজ্ঞান এবং অ্যাপ্লিকেশন কেন্দ্রের একজন পোস্টডক্টরাল ফেলো; এবং ম্যাথিউ কোয়ান, ইনস্টিটিউট অফ সায়েন্স অ্যান্ড টেকনোলজি অস্ট্রিয়ার একজন গণিতবিদ। "এখানে বেশ আকর্ষণীয়, বেশ কঠিন প্রযুক্তিগত কাজ ছিল।"
উদাহরণস্বরূপ, পুনরাবৃত্তিমূলক শোষণের অন্যান্য অ্যাপ্লিকেশনগুলিতে, একবার আপনি একটি সেট কভার করা শেষ করে ফেললে — হয় ত্রিভুজ সহ, স্টেইনার ট্রিপল সিস্টেমের জন্য, বা অন্যান্য সমস্যার জন্য অন্যান্য কাঠামোর সাথে — আপনি এটিকে মোকাবেলা করা বিবেচনা করতে পারেন এবং এটি ভুলে যেতে পারেন। তবে এরদসের শর্ত চার গণিতবিদকে তা করতে বাধা দেয়। ত্রিভুজগুলির একটি সমস্যাযুক্ত ক্লাস্টার সহজেই একাধিক শোষক সেট থেকে নোডকে জড়িত করতে পারে।
"একটি ত্রিভুজ যা আপনি 500 ধাপ আগে বেছে নিয়েছিলেন, এটি সম্পর্কে কীভাবে ভাবতে হয় তা আপনাকে মনে রাখতে হবে," বলেছেন সাহনি৷
চারটি অবশেষে যা বের করেছিল তা হল যে তারা যদি তাদের ত্রিভুজগুলি সাবধানে বেছে নেয় তবে তারা প্রতিটি ছোট জিনিসের উপর নজর রাখার প্রয়োজনীয়তাকে এড়াতে পারে। "যা করা ভাল তা হল 100টি ত্রিভুজের যে কোনও ছোট সেট সম্পর্কে চিন্তা করা এবং গ্যারান্টি দেওয়া যে ত্রিভুজের সেটটি সঠিক সম্ভাবনার সাথে বেছে নেওয়া হয়েছে," সাহনি বলেছিলেন।
নতুন কাগজের লেখকরা আশাবাদী যে তাদের কৌশল এই একটি সমস্যা অতিক্রম করা যেতে পারে. তাদের আছে ইতিমধ্যে তাদের কৌশল প্রয়োগ করেছে সম্পর্কে একটি সমস্যা ল্যাটিন স্কোয়ার, যা একটি সুডোকু ধাঁধার সরলীকরণের মত।
এর বাইরে, বেশ কয়েকটি প্রশ্ন রয়েছে যা অবশেষে শোষণের পদ্ধতিতে পরিণত হতে পারে, কোয়ান বলেছেন। "কম্বিনেটরিক্সে অনেক সমস্যা আছে, বিশেষ করে ডিজাইন থিওরিতে, যেখানে র্যান্ডম প্রসেস সত্যিই শক্তিশালী টুল।" এরকম একটি সমস্যা, Ryser-Brualdi-Stein অনুমান, এছাড়াও ল্যাটিন স্কোয়ার সম্পর্কে এবং 1960 সাল থেকে একটি সমাধানের জন্য অপেক্ষা করছে।
যদিও শোষণের আরও বিকাশের প্রয়োজন হতে পারে এই সমস্যাটি হ্রাস করার আগে, এটি 30 আগে এর সূচনা থেকে অনেক দূর এগিয়ে গেছে, বলেছেন মায়া স্টেইন, চিলি বিশ্ববিদ্যালয়ের গাণিতিক মডেলিং কেন্দ্রের উপ-পরিচালক। "এটি এমন কিছু যা দেখতে সত্যিই দুর্দান্ত, এই পদ্ধতিগুলি কীভাবে বিকশিত হয়।"