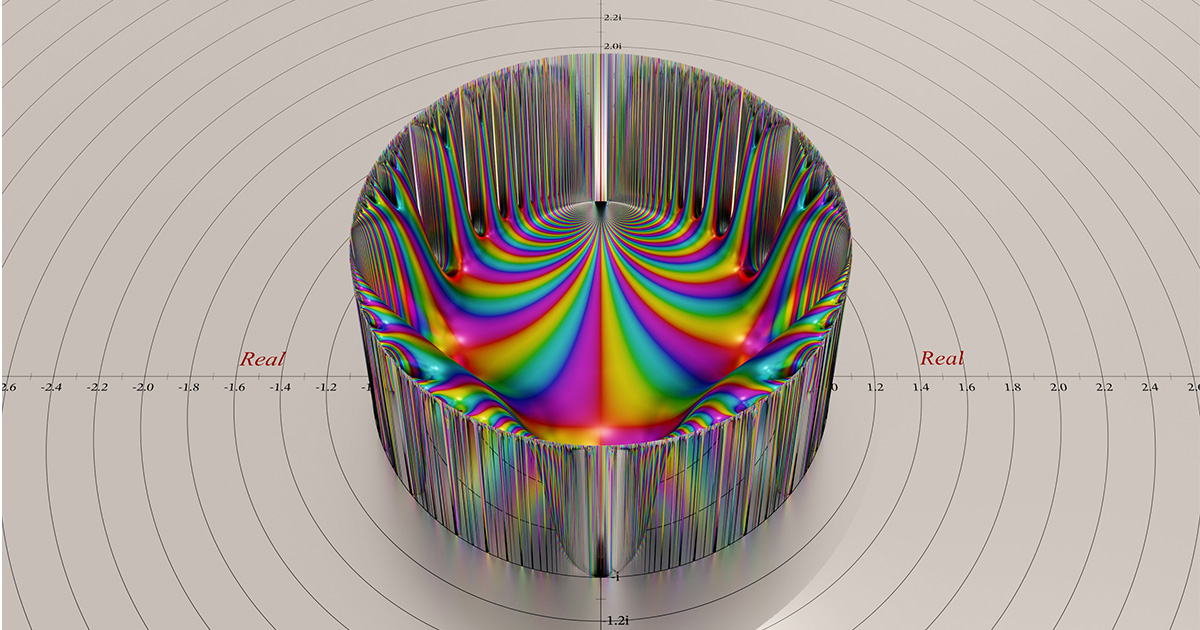
परिचय
एक नए प्रमाण में, लंबे समय से उपेक्षित एक गणितीय वस्तु आखिरकार सुर्खियों में आ गई है।
पहली नज़र में, मॉड्यूलर रूप - फ़ंक्शन जिनकी प्रचुर समरूपता ने सदियों से गणितज्ञों को आकर्षित किया है - ने पर्याप्त से अधिक ध्यान आकर्षित किया है। वे सभी प्रकार की समस्याओं में उभरते हैं: वे एंड्रयू विल्स के 1994 के फ़र्मेट के अंतिम प्रमेय के प्रमाण में एक प्रमुख घटक थे, जिसने संख्या सिद्धांत में सबसे बड़े खुले प्रश्नों में से एक को हल किया। वे इसमें केन्द्रीय भूमिका निभाते हैं लैंगलैंड्स कार्यक्रम, "गणित का एक भव्य एकीकृत सिद्धांत" विकसित करने का एक सतत प्रयास। इनका उपयोग स्ट्रिंग सिद्धांत और क्वांटम भौतिकी में मॉडल का अध्ययन करने के लिए भी किया गया है।
लेकिन इन सन्दर्भों में जो मॉड्यूलर रूप उत्पन्न होते हैं वे एक विशेष प्रकार के होते हैं। तथाकथित "सर्वांगसमता" मॉड्यूलर फॉर्म अतिरिक्त संरचना का दावा करते हैं जिससे उनका अध्ययन करना आसान हो जाता है। लेकिन अधिक सामान्य "गैर-अनुरूपता" मॉड्यूलर रूपों की संख्या उनके अनुकूल सर्वांगसम समकक्षों से बहुत अधिक है। "यदि आप संभाव्यता 1 के साथ एक यादृच्छिक मॉड्यूलर रूप लेते हैं, तो यह गैर-अनुरूपता है," कहा कैमरून फ़्रैंक, कनाडा में मैकमास्टर विश्वविद्यालय में गणितज्ञ। “जब तक आपके पास एक सर्वांगसम मॉड्यूलर फॉर्म का सामना करने का वास्तव में कोई अच्छा कारण नहीं है, आप इसकी उम्मीद नहीं करेंगे। वे बहुत दुर्लभ हैं।"
और फिर भी गणितज्ञ उनकी सर्वव्यापकता के बावजूद, गैर-अनुरूप मॉड्यूलर रूपों के बारे में बहुत कम जानते हैं। "वे पूरी तरह से रहस्यमय हैं," उन्होंने कहा एंथोनी शॉल, कैम्ब्रिज विश्वविद्यालय में गणितज्ञ। कार्यों के ऐसे सामान्य वर्ग के बारे में सर्वव्यापी बयान देना न केवल मुश्किल है, बल्कि मॉड्यूलर रूपों का अध्ययन करने के लिए विकसित किए गए उपकरण गैर-अनुरूपता मामले में विफल हो जाते हैं। इसने गणितज्ञों को इस बात को लेकर अनिश्चित बना दिया है कि उन्हें क्या साबित करने की कोशिश करनी चाहिए।
परिचय
हालाँकि, गैर-अनुरूप मॉड्यूलर रूपों के बारे में एक प्रमुख अनुमान लंबे समय से सामने आया है: रेगिस्तान में एक अकेला, अस्थिर साइनपोस्ट।
1968 में, गणितज्ञ ओलिवर एटकिन और पीटर स्विनर्टन-डायर ने देखा कि गैर-अनुरूप मॉड्यूलर रूपों में एक विशेष रूप से विशिष्ट संपत्ति होती है जो उन्हें सर्वांगसम मॉड्यूलर रूपों से अलग करती है। दोनों को अलग बताने का इतना स्पष्ट तरीका होना "वास्तव में बहुत आश्चर्यजनक है," उन्होंने कहा जेफ्री मेसन, कैलिफोर्निया विश्वविद्यालय, सांता क्रूज़ में गणितज्ञ। सर्वांगसमता और गैर-सर्वांगसमता मॉड्यूलर रूप बहुत भिन्न होते हैं, क्योंकि गैर-सर्वांगसमता मॉड्यूलर रूपों में समरूपता का अभाव होता है जो सर्वांगसमता मॉड्यूलर रूपों में होता है। लेकिन ये अंतर, हालांकि महत्वपूर्ण हैं, सूक्ष्म हो सकते हैं और इनका पता लगाना मुश्किल हो सकता है।
यहाँ, अचानक, इन मतभेदों का स्पष्ट प्रमाण स्पष्ट हो गया।
एटकिन और स्विनर्टन-डायर के अवलोकन को बाद में "अनबाउंड डिनोमिनेटर्स" अनुमान के रूप में जाना जाने लगा। यदि यह सच है, तो यह गणितज्ञों को गैर-अनुरूप वस्तुओं के बड़े पैमाने पर अज्ञात क्षेत्र में अपना पहला पैर जमाने की अनुमति देगा। और यह पहचानने का एक आसान तरीका प्रदान करके कि दिया गया मॉड्यूलर रूप किस वर्ग से संबंधित है, अनुमान सैद्धांतिक भौतिकी में एक प्रमुख कार्यक्रम भी डाल सकता है - जिसका उद्देश्य कण इंटरैक्शन के मॉडल को समझना है जिसे अनुरूप क्षेत्र सिद्धांत कहा जाता है - मजबूत गणितीय आधार पर।
लेकिन 50 साल से भी ज्यादा समय तक कोई भी इसे साबित नहीं कर सका। अंततः, 2021 के अंत में, गणितज्ञों की एक तिकड़ी सफल हुई. ऐसा प्रतीत होता है कि उनका प्रमाण कहीं से भी आया है, ऐसी तकनीकों का उपयोग करते हुए जिनकी किसी ने अध्ययन के इस क्षेत्र में देखने की उम्मीद नहीं की थी। गणितज्ञ और भौतिक विज्ञानी अब उस कार्य के परिणामों का पता लगाना शुरू कर रहे हैं।
समरूपता और संरचना
गैर-अनुरूपता मॉड्यूलर रूपों को हमेशा हाशिये पर नहीं रखा गया था।
19वीं शताब्दी में, गणितज्ञ मॉड्यूलर रूपों का एक सिद्धांत विकसित करना शुरू ही कर रहे थे। यह एक विशेष प्रकार के अत्यधिक सममित फ़ंक्शन को दिया गया नाम था - वह जो जटिल विमान के ऊपरी आधे हिस्से के रूप में जाने जाने वाले डोमेन में रहता है।
सम्मिश्र तल सम्मिश्र संख्याओं को रेखांकन करने का एक तरीका है, जिसके दो भाग होते हैं: वास्तविक और काल्पनिक। एक मॉड्यूलर रूप इसके इनपुट जटिल संख्याओं को लेता है जिनका काल्पनिक भाग सकारात्मक होता है, जो विमान के ऊपरी आधे हिस्से के अनुरूप होता है। (ऊपरी आधे तल को यूनिट डिस्क के आंतरिक भाग में आसानी से मैप किया जा सकता है; मॉड्यूलर रूपों को अक्सर इस मैपिंग का उपयोग करके चित्रित किया जाता है।)
परिचय
मॉड्यूलर रूपों की कई समरूपताओं को 2-बाय-2 मैट्रिक्स के विशेष संग्रह, या "समूहों" के संदर्भ में परिभाषित किया गया है - चार संख्याओं के वर्ग सरणी। मॉड्यूलर रूपों में, वे चार संख्याएँ हमेशा पूर्णांक होती हैं। महत्वपूर्ण रूप से, मैट्रिक्स से जुड़ी एक संख्या जो इसके कुछ गुणों को निर्धारित करती है - जिसे निर्धारक कहा जाता है - 1 होनी चाहिए।
मैट्रिक्स के ऐसे अनंत सेट हैं। कुछ समूहों में, आव्यूहों का वर्णन अपेक्षाकृत सरल नियमों द्वारा किया जा सकता है। उदाहरण के लिए, सभी आव्यूहों में, ऊपर दाएँ और नीचे बाएँ प्रविष्टियाँ सम हो सकती हैं, जबकि अन्य दो प्रविष्टियाँ विषम हैं। या शायद ऊपरी दाएँ और निचले बाएँ प्रविष्टियाँ 11 से विभाज्य हैं, जबकि अन्य दो प्रविष्टियाँ 1 के गुणज से 11 अधिक हैं।
जिन समूहों को इस प्रकार के संबंधों द्वारा परिभाषित किया जा सकता है - और ऐसे समूहों से जुड़े मॉड्यूलर रूप - बहुत अध्ययन किए गए सर्वांगसमता वाले हैं।
लेकिन वे भूसे के ढेर में सुइयों की तरह हैं: 2-बाय-2 मैट्रिक्स के अधिकांश संग्रहों को इस तरह से अच्छे नियमों द्वारा चित्रित नहीं किया जा सकता है, जिससे वे और उनके संबंधित मॉड्यूलर रूप असंगत हो जाते हैं।
1930 के दशक के अंत तक - द्वितीय विश्व युद्ध की शुरुआत के आसपास - ऐसा नहीं था कि सर्वांगसमता मॉड्यूलर रूपों के अध्ययन ने गैर-सर्वांगसमता वाले रूपों के अध्ययन को ग्रहण करना शुरू कर दिया। तभी जर्मन गणितज्ञ एरिच हेके ने एक टूलबॉक्स विकसित किया जो उन्हें मॉड्यूलर रूपों के कई गुणों को पिन करने और उन्हें अन्य महत्वपूर्ण गणितीय वस्तुओं के साथ जोड़ने की अनुमति देगा।
हेके के तरीके केवल सर्वांगसम समूहों और उनके मॉड्यूलर रूपों के लिए काम करते थे। गैर-अनुरूप समूहों में उस अतिरिक्त संरचना का अभाव था जो हेके के टूलबॉक्स को प्रभावी बनाती थी। फ़्रैंक ने कहा, "सर्वांगसम दुनिया में आपके पास जो चीज़ है वह गैर-समान दुनिया में जाने पर बाहर चली जाती है।"
और इसलिए ऐसा प्रतीत हुआ कि गैर-अनुरूप मॉड्यूलर रूपों को हमेशा अनदेखा किया जाना तय था। इसका मतलब यह नहीं है कि सतह के ठीक नीचे छिपी उनकी अपनी कोई विशेष संरचना नहीं थी। जैसा कि स्विनर्टन-डायर के सहयोगी ब्रायन बिर्च ने एक बार लिखा था, "हालांकि संरचना अधिक रहस्यमय है, लेकिन यह लगभग उतनी ही समृद्ध प्रतीत होती है।" लेकिन जब उस संरचना तक पहुँचने की बात आई, तो गणितज्ञों को नुकसान हुआ। उन्हें यह भी नहीं पता था कि कहां से शुरुआत करें.
एटकिन और स्विनर्टन-डायर दर्ज करें।
एक सुव्यवस्थित मानदंड
दोनों गणितज्ञ गैर-अनुरूप मॉड्यूलर रूपों के बारे में और अधिक जानना चाहते थे, और जो भी रहस्य वे छिपा रहे हों, उसके बारे में और जानना चाहते थे।
"गणित हमेशा इसी तरह आगे बढ़ता है," कहा विनी ली, पेंसिल्वेनिया स्टेट यूनिवर्सिटी में गणितज्ञ। “आप बहुत विशेष गुणों और अधिक संरचना वाली चीज़ों का अध्ययन करते हैं। फिर आप इसका सामान्यीकरण करें, यह समझने की कोशिश करें कि कौन से गुण आगे बढ़ते हैं और कौन से नहीं।"
किसी दिए गए मॉड्यूलर रूप का अध्ययन करने के लिए, गणितज्ञ अक्सर इसे एक अनंत योग के रूप में दर्शाते हैं जिसे क्यू-विस्तार (एक विशेष प्रकार की शक्ति श्रृंखला) कहा जाता है, फिर उस विस्तार के गुणांक का विश्लेषण करते हैं। यह पहले से ही ज्ञात था कि यदि कोई दिया गया मॉड्यूलर रूप सर्वांगसम है, तो गुणांक में हर होते हैं जो कभी भी कुछ निश्चित मान से बड़े नहीं होते हैं।
1960 के दशक में, एटकिन और स्विनर्टन-डायर ने मॉड्यूलर रूपों के स्कोर और स्कोर के लिए क्यू-विस्तार की गणना की। जैसे ही उन्होंने ऐसा किया, उन्होंने देखा कि यदि एक मॉड्यूलर रूप असंगत था, तो उसके संबंधित अनुक्रम में हर बिना किसी सीमा के बढ़ते रहे। "वे वास्तव में इन रहस्यमय गैर-अनुरूपता रूपों के बारे में कुछ कह सकते हैं," उन्होंने कहा युन्किंग तांग, कैलिफोर्निया विश्वविद्यालय, बर्कले में गणितज्ञ।
क्या वास्तव में दो प्रकार के मॉड्यूलर रूपों को अलग करना इतना आसान हो सकता है?
गणितज्ञों ने 1968 में कैलिफ़ोर्निया में एक सम्मेलन में अपने अवलोकन का उल्लेख किया, जिसमें सुझाव दिया गया कि असंबद्ध हर गैर-अनुरूप मॉड्यूलर रूपों की एक सार्वभौमिक पहचान हो सकते हैं। अनुमान "बहुत आश्चर्यजनक" था, ने कहा जॉन वोइट, डार्टमाउथ कॉलेज में गणितज्ञ। "यह हमें यह तय करने के लिए एक स्पष्ट मानदंड देता है कि मॉड्यूलर फॉर्म एक सर्वांगसमता समूह से संबंधित है या नहीं" - संख्या सिद्धांतकारों के लिए एक बहुत ही सुविधाजनक लिटमस टेस्ट, और कुछ ऐसा जो अन्य संदर्भों में पता लगाना मुश्किल हो सकता है।
उन्होंने आगे कहा, "यह सच होने के लिए लगभग बहुत अच्छा है।" "कोई वास्तव में उस तरह के चमत्कार की उम्मीद नहीं करता है।"
वास्तव में, कोई भी असीमित हर अनुमान को सिद्ध नहीं कर सका। ली और कुछ अन्य लोग थे दिखाने में सक्षम यह सच था विशिष्ट परिवार गैर-अनुरूप मॉड्यूलर रूपों का, लेकिन गणितज्ञों को पता नहीं था कि सामान्य कथन से कैसे निपटा जाए।
फिर सितंबर 2021 में, टैंग, साथ में फ़्रैंक कैलेगरी शिकागो विश्वविद्यालय के और वेसेलिन दिमित्रोव इंस्टीट्यूट फॉर एडवांस्ड स्टडी ने 50 पेज का प्रमाण पोस्ट किया। "यह आश्चर्यजनक और वास्तव में अप्रत्याशित था," फ्रैंक ने कहा। "ऐसा लगा जैसे समुदाय के पास इस समस्या से निपटने के बारे में कोई विचार ही नहीं था।"
लेखकों को उम्मीद है कि उनका पेपर रेगिस्तान में उस साइनपोस्ट को एक पूर्ण सड़क नेटवर्क में विकसित करने की दिशा में पहला कदम है। दिमित्रोव ने कहा, "हम संख्या सिद्धांत के इस भाग में इसके सबसे आसान प्रश्न का उत्तर प्रदान करके अपना मामूली योगदान देते हैं।"
पुराने तरीकों पर वापस जाएँ
कालेगारी, दिमित्रोव और टैंग ने असीमित हर अनुमान को हल करने का प्रयास नहीं किया। 2019 के अंत में, वे यह दिखाने की उम्मीद कर रहे थे कि एक निश्चित संख्या (रीमैन ज़ेटा फ़ंक्शन के एनालॉग का मान) तर्कहीन थी - कि, 2 के वर्गमूल की तरह, इसे अंश के रूप में नहीं लिखा जा सकता है। (उनका अंतिम लक्ष्य यह साबित करना है कि यह संख्या और इसके जैसे अन्य संख्याएँ पारलौकिक हैं, जिसका अर्थ है कि, संख्याओं की तरह π और e, उन्हें पूर्णांक गुणांक वाले बहुपद समीकरण के समाधान के रूप में नहीं लिखा जा सकता है।)
पहली नज़र में, यह समस्या पूरी तरह से असंबंधित है। लेकिन 1 जनवरी, 2021 को, दिमित्रोव ने दूसरों को एक ईमेल भेजकर नए साल का स्वागत किया, जिसमें उन्होंने "एक इच्छाधारी विचार" का वर्णन किया: शायद पिछले वर्ष में वे जो तकनीकें विकसित कर रहे थे, उन्हें असीमित भाजक अनुमान को साबित करने के लिए पुन: उपयोग किया जा सकता है।
उन्होंने इसे एक मौका दिया. सात महीने के भीतर, उनके पास इसका सबूत था।
परिचय
सबसे पहले, उन्होंने दो स्थानों पर विचार किया: परिबद्ध हर वाले सभी मॉड्यूलर रूपों का स्थान, और सभी सर्वांगसम मॉड्यूलर रूपों का स्थान। असीमित हर अनुमान के अनुसार, वे दो स्थान समान होने चाहिए। चूँकि रिक्त स्थान कुछ गुणों को संतुष्ट करते थे, गणितज्ञों को केवल यह दिखाना था कि वे एक ही आकार के थे। ऐसा करने से स्वतः ही उनकी समतुल्यता का पता चल जाएगा।
कैलेगरी, दिमित्रोव और तांग दूसरे स्थान के आकार की गणना अपेक्षाकृत आसानी से कर सकते थे, जिससे सर्वांगसमता मॉड्यूलर रूपों की एक प्रकार की अनुमानित गणना प्राप्त हो सकती थी। लेकिन पहले स्थान के आकार का अनुमान लगाना बहुत कठिन था। उन्हें कई अलग-अलग तकनीकों को संयोजित करना पड़ा - जिनमें ट्रान्सेंडैंटल नंबर सिद्धांत की तकनीकें भी शामिल थीं।
उन विधियों का उपयोग करके, उन्होंने दिखाया कि परिबद्ध हर वाले मॉड्यूलर रूपों का स्थान अधिकतम एक निश्चित आकार का हो सकता है। वह अधिकतम आकार सर्वांगसम मॉड्यूलर रूपों के स्थान के आकार से थोड़ा बड़ा था। फिर भी, यह कदम "वास्तव में प्रमाण का मूल" साबित हुआ, उन्होंने कहा जीन-बेनोइट बोस्ट, पेरिस-सैकले विश्वविद्यालय में गणितज्ञ। "ऐसा करने के लिए आपको बहुत धैर्य की आवश्यकता है।" (कैलेगारी, दिमित्रोव और तांग ने कुछ अलग-अलग तरीकों से अंतरिक्ष के आकार पर इसे साबित किया, संभवतः उनकी तकनीकों को अधिक व्यापक अनुप्रयोग दिए।)
“यह बहुत, बहुत शास्त्रीय, सुंदर गणित है, जिसमें 19वीं सदी की झलक है,” कहा जेवियर फ्रेसन, फ़्रांस में इकोले पॉलिटेक्निक में गणितज्ञ।
तब तिकड़ी को दोनों स्थानों के बीच के अंतर को कम करने की आवश्यकता थी। ऐसा करने से यह स्थापित हो जाएगा कि परिबद्ध हर वाले किसी भी मॉड्यूलर रूप का सर्वांगसम होना आवश्यक है।
परिचय
इसलिए उन्होंने इसके विपरीत मान लिया: कि परिबद्ध हर के साथ एक गैर-अनुरूपता मॉड्यूलर रूप मौजूद है। परिभाषा के अनुसार, यह उस अंतर में रहेगा जिसे कैलेगारी, दिमित्रोव और टैंग बंद करने की कोशिश कर रहे थे। फिर तीनों ने दिखाया कि इस गैर-अनुरूप मॉड्यूलर रूप का अस्तित्व स्वचालित रूप से बंधे हुए हर के साथ कई अन्य गैर-अनुरूप मॉड्यूलर रूपों के अस्तित्व को दर्शाता है। ऐसा लग रहा था मानो उस एक बीज से पूरा जंगल उग आया हो।
लेकिन उन्होंने अंतर का अधिकतम आकार पहले ही स्थापित कर लिया था - और यह इतने सारे गैर-अनुरूप रूपों को फिट करने के लिए बहुत छोटा था।
जिसका अर्थ था कि ऐसा एक भी रूप अस्तित्व में नहीं हो सकता। उन्होंने एटकिन और स्विनर्टन-डायर के दशकों पुराने अनुमान को साबित कर दिया।
गणितज्ञों को कार्य में उपयोग की गई तकनीकें परिणाम से भी अधिक दिलचस्प लगती हैं। शोल ने कहा, "इन विचारों का उपयोग मॉड्यूलर रूपों के अंकगणित का अध्ययन करने में पहले कभी नहीं किया गया है।"
जैसा कि वोइट बताते हैं, हालांकि मॉड्यूलर रूपों का अध्ययन जटिल विश्लेषण के क्षेत्र के हिस्से के रूप में शुरू हुआ, वर्तमान कार्य संख्या सिद्धांत और बीजगणितीय ज्यामिति के दायरे में रहा है। उन्होंने कहा, नया पेपर जटिल विश्लेषण की ओर वापसी का प्रतीक है: "यह एक ताज़ा पुराना परिप्रेक्ष्य है।"
नये सिद्धांतों की खोज
केवल गणितज्ञ ही असीमित हर अनुमान को लेकर उत्साहित नहीं हैं। यह सैद्धांतिक भौतिकी में भी दिखाई देता है।
1970 के दशक में, एटकिन और स्विनर्टन-डायर द्वारा शुरू की गई कहानी के समानांतर एक और कहानी सामने आ रही थी। गणितज्ञों के पास था एक अजीब संबंध देखा एक वस्तु के बीच जिसे राक्षस समूह कहा जाता है और एक मॉड्यूलर रूप जिसे कहा जाता है j-समारोह। के गुणांक j-फ़ंक्शन ने राक्षस समूह के कुछ गुणों को सटीक रूप से प्रतिबिंबित किया।
बाद के शोध से पता चला कि यह संबंध इस तथ्य के कारण था कि समूह और मॉड्यूलर रूप दोनों कण इंटरैक्शन के एक महत्वपूर्ण मॉडल से संबंधित थे, जिसे द्वि-आयामी अनुरूप क्षेत्र सिद्धांत कहा जाता है।
लेकिन अनुरूप क्षेत्र सिद्धांत जिसने राक्षस समूह को इससे जोड़ा j-फंक्शन अनंत संख्या में अनुरूप क्षेत्र सिद्धांतों का सिर्फ एक उदाहरण था। और जबकि ये सिद्धांत उस ब्रह्मांड का वर्णन नहीं करते हैं जिसमें हम रहते हैं, उन्हें समझने से नई अंतर्दृष्टि मिल सकती है कि अधिक यथार्थवादी क्वांटम क्षेत्र सिद्धांत कैसे व्यवहार कर सकते हैं।
और इसलिए भौतिकविदों ने उनके संबंधित मॉड्यूलर रूपों को देखकर अनुरूप क्षेत्र सिद्धांतों का अध्ययन करना जारी रखा है। (इस संदर्भ में, भौतिक विज्ञानी एक मॉड्यूलर रूप की अधिक सामान्य धारणा का उपयोग करते हैं, जिसे वेक्टर-मूल्यवान मॉड्यूलर रूप कहा जाता है।)
किसी विशेष अनुरूप क्षेत्र सिद्धांत के साथ क्या हो रहा है, इस पर नियंत्रण पाने के लिए, आपको यह दिखाना होगा कि इसका मॉड्यूलर रूप सर्वांगसमता है, जैसा कि कहा गया है माइकल तुइटेआयरलैंड में गॉलवे विश्वविद्यालय के गणितज्ञ और सैद्धांतिक भौतिक विज्ञानी। फिर आप अनुरूप क्षेत्र सिद्धांतों का वर्णन करना शुरू कर सकते हैं, और यहां तक कि नए सिद्धांतों की खोज भी कर सकते हैं जिन्हें आप खोजना नहीं जानते थे। यह सभी अनुरूप क्षेत्र सिद्धांतों को वर्गीकृत करने के चल रहे प्रयास के लिए विशेष रूप से महत्वपूर्ण है - एक परियोजना जिसे भौतिकविदों ने मॉड्यूलर बूटस्ट्रैप करार दिया है।
मेसन ने कहा, "एक बार जब आप जान जाते हैं कि यह एक अनुरूप मॉड्यूलर रूप है, तो यह आपको इस कार्यक्रम में भारी प्रगति करने में सक्षम बनाता है।"
भौतिकविदों ने एक ढांचा विकसित किया है जो उन्हें उन मॉड्यूलर रूपों के लिए इस अनुरूपता संपत्ति को मानने की अनुमति देता है जिनका वे अध्ययन कर रहे हैं। लेकिन यह एक कठोर गणितीय प्रमाण के समान नहीं है - और जबकि अन्य गणितज्ञ बाद में सक्षम थे ऐसा कोई प्रमाण दीजिए, उनका तर्क केवल कुछ सेटिंग्स में ही काम करता था। मेसन के अनुसार, इसमें सर्वांगसमता की ओर "एक बहुत ही पेचीदा, जटिल रास्ता" भी शामिल था, हालांकि उन्होंने यह भी बताया कि इस पेचीदा रास्ते से महत्वपूर्ण अंतर्दृष्टि प्राप्त होती है।
कालेगारी, दिमित्रोव और टैंग के असीमित हर के प्रमाण से यह सब स्पष्ट हो जाता है। ऐसा इसलिए है, क्योंकि जैसा कि यह पता चला है, अनुरूप क्षेत्र सिद्धांतों से जुड़े मॉड्यूलर रूपों में हमेशा पूर्णांक गुणांक होते हैं। परिभाषा के अनुसार, पूर्णांकों का हर 1 होता है, जिसका अर्थ है कि उनके हर हमेशा परिबद्ध होते हैं। और चूंकि असंबद्ध हर अनुमान बताता है कि परिबद्ध हर केवल सर्वांगसमता मॉड्यूलर रूपों से जुड़े होते हैं, इसलिए अब धारणा बनाने की कोई आवश्यकता नहीं है। "आपको [अनुरूप क्षेत्र सिद्धांतों] के बारे में कुछ भी जानने की ज़रूरत नहीं है," तांग ने कहा। नया प्रमाण स्वचालित रूप से इन सभी मामलों के लिए निःशुल्क प्रदान करता है।
"यह कुछ ऐसा है जो दशकों से हवा में है," बोस्ट ने कहा। अब आख़िरकार इसका समाधान हो गया है.
"यह वास्तव में एक चमत्कार है," मेसन ने कहा। "यह इस तथ्य से चमत्कारिक रूप से निकलता है कि ये अनुक्रम पूर्णांक हैं।"
उन्होंने पहले ही परिणाम को अपने काम में लागू करना शुरू कर दिया है। उन्होंने कहा, "जिस दिन से वह पेपर छपा है, मैं उसका उपयोग कर रहा हूं।" “यह उन परिणामों के लिए एक बहुत ही स्वागत योग्य शॉर्टकट प्रदान करता है जिन्हें मैं हल करना चाहता हूं। ...यह बड़ी मात्रा में संभावित काम को ख़त्म कर रहा है जिसके माध्यम से मैं अपना रास्ता नहीं देख सका।
यह मॉड्यूलर बूटस्ट्रैप प्रोग्राम और अन्य परिणामों को मजबूत गणितीय आधार पर भी रखता है। मेसन ने कहा, "यह गणितज्ञों को [पिछले] परिणामों को फिर से साबित करने या उन पर विश्वास करने की अनुमति देगा।"
"मुझे लगता है कि इसका वास्तव में प्रभाव पड़ने वाला है, विशेष रूप से गणित के पक्ष पर, बस वास्तव में, वास्तव में चीजों को बांधने के लिए, यह समझने के लिए कि वास्तव में क्या हो रहा है," ट्युइट ने कहा।
गणितीय अतिक्रमण
जिस वर्ष से उन्होंने अपना प्रमाण पोस्ट किया है, कैलेगारी, दिमित्रोव और टैंग ने अपना सहयोग जारी रखा है। वे अब पारलौकिक संख्या सिद्धांत में समस्याओं के प्रकार पर लौट आए हैं जिन्होंने मूल रूप से अनुमान में उनकी रुचि जगाई थी। टैंग ने कहा, "हमने जो शुरू किया था उसे पूरा करने की कोशिश कर रहे हैं।" वास्तव में, वे पहले ही अपनी तकनीकों का उपयोग यह साबित करने के लिए कर चुके हैं कि रुचि की कई संख्याएँ तर्कहीन हैं।
"वे वास्तव में [विधि] को सीमा तक बढ़ा रहे हैं," फ्रेसन ने कहा। "मैं वास्तव में इसे लेकर बहुत उत्साहित हूं।"
ये विधियाँ संख्या सिद्धांत की अन्य समस्याओं पर भी लागू हो सकती हैं।
तकनीकों के अलावा, असंबद्ध हर अनुमान का समाधान गैर-अनुरूपता मॉड्यूलर रूपों की बेहतर समझ हासिल करने के प्रयास में पहले बड़े मील के पत्थर में से एक है। फ़्रैंक ने कहा, "यह एक अद्भुत उपलब्धि है कि हम इस तरह से गैर-अनुरूपता रूपों पर कुछ प्रगति कर सकते हैं।" "मैं अगले 10, 20 वर्षों तक यह देखने के लिए उत्साहित हूं कि क्या होता है।"
ली, वोइट और अन्य पहले से ही इन रहस्यमय मॉड्यूलर रूपों के हर में दिखाई देने वाली संख्याओं के प्रकार में पैटर्न की तलाश शुरू कर रहे हैं। उन्हें उम्मीद है कि ऐसा करने से उन्हें गहरी संरचना के संकेत मिल सकते हैं।
ली ने कहा, "यह असीमित हर अनुमान केवल शुरुआत थी।"
- एसईओ संचालित सामग्री और पीआर वितरण। आज ही प्रवर्धित हो जाओ।
- प्लेटोब्लॉकचैन। Web3 मेटावर्स इंटेलिजेंस। ज्ञान प्रवर्धित। यहां पहुंचें।
- स्रोत: https://www.quantamagazine.org/long-sought-math-proof-unlocks-more-mysterious-modular-forms-20230309/
- :है
- ][पी
- $यूपी
- 1
- 10
- 11
- 1994
- 20 साल
- 2019
- 2021
- 50 वर्षों
- a
- योग्य
- About
- AC
- तक पहुँचने
- अनुसार
- उपलब्धि
- वास्तव में
- जोड़ा
- अतिरिक्त
- उन्नत
- आकाशवाणी
- सब
- की अनुमति देता है
- पहले ही
- हमेशा
- अद्भुत
- राशि
- विश्लेषण
- विश्लेषण करें
- और
- एंड्रयू
- अन्य
- जवाब
- अलग
- स्पष्ट
- छपी
- उपयुक्त
- अनुप्रयोगों
- लागू
- दृष्टिकोण
- हैं
- क्षेत्र
- तर्क
- चारों ओर
- AS
- सहयोगी
- जुड़े
- ग्रहण
- At
- ध्यान
- लेखकों
- स्वतः
- BE
- सुंदर
- क्योंकि
- से पहले
- शुरू
- मानना
- बर्कले
- बेहतर
- के बीच
- बड़ा
- बड़ा
- सबसे बड़ा
- बिट
- जूते का फीता
- तल
- सीमा
- टूटना
- व्यापक
- ब्रयान
- by
- गणना
- कैलिफ़ोर्निया
- बुलाया
- कैंब्रिज
- कर सकते हैं
- कनाडा
- नही सकता
- ले जाना
- मामला
- मामलों
- केंद्रीय
- सदी
- कुछ
- विशेषता
- शिकागो
- कक्षा
- वर्गीकृत
- समापन
- सहयोग
- संग्रह
- कॉलेज
- गठबंधन
- कैसे
- समुदाय
- पूरी तरह से
- जटिल
- सम्मेलन
- अनुमान
- संबंध
- Consequences
- माना
- प्रसंग
- संदर्भों
- निरंतर
- योगदान
- सुविधाजनक
- इसी
- सका
- फ़सल
- महत्वपूर्ण
- महत्वपूर्ण
- वर्तमान
- कटौती
- कटाई
- दिन
- दशकों
- तय
- और गहरा
- परिभाषित
- बचाता है
- वर्णन
- वर्णित
- DESERT
- के बावजूद
- निर्धारित
- विकसित करना
- विकसित
- विकासशील
- डीआईडी
- मतभेद
- विभिन्न
- मुश्किल
- अन्य वायरल पोस्ट से
- विशिष्ट
- नहीं करता है
- कर
- डोमेन
- dont
- द्वारा
- नीचे
- करार दिया
- आसान
- सबसे आसान
- आसानी
- प्रभावी
- प्रयास
- ईमेल
- सक्षम बनाता है
- विशाल
- पर्याप्त
- पूरी तरह से
- विशेष रूप से
- स्थापित करना
- स्थापित
- आकलन
- और भी
- सबूत
- ठीक ठीक
- उदाहरण
- उत्तेजित
- मौजूद
- विस्तार
- उम्मीद
- अपेक्षित
- बताते हैं
- का पता लगाने
- अतिरिक्त
- चेहरा
- खेत
- अंत में
- खोज
- खत्म
- प्रथम
- फिट
- तय
- इस प्रकार है
- के लिए
- वन
- प्रपत्र
- रूपों
- अंश
- ढांचा
- फ्रैंक
- फ्रांस
- मुक्त
- अनुकूल
- से
- पूर्ण
- समारोह
- कार्यों
- लाभ
- अन्तर
- सामान्य जानकारी
- जर्मन
- मिल
- दी
- देता है
- देते
- झलक
- Go
- लक्ष्य
- चला जाता है
- जा
- अच्छा
- बहुत
- जमीन
- समूह
- समूह की
- बढ़ रहा है
- वयस्क
- आधा
- मुट्ठी
- संभालना
- हो जाता
- है
- होने
- दिल
- अत्यधिक
- संकेत
- आशा
- उम्मीद कर रहा
- कैसे
- How To
- तथापि
- एचटीएमएल
- http
- HTTPS
- विशाल
- i
- विचार
- विचारों
- समान
- काल्पनिक
- प्रभाव
- अस्पष्ट
- महत्वपूर्ण
- in
- अन्य में
- सहित
- अनंत
- निवेश
- अंतर्दृष्टि
- संस्थान
- बातचीत
- ब्याज
- आंतरिक
- शामिल
- आयरलैंड
- IT
- आईटी इस
- खुद
- जनवरी
- जेपीजी
- सिर्फ एक
- कुंजी
- बच्चा
- जानना
- जानने वाला
- रंग
- बड़े पैमाने पर
- बड़ा
- पिछली बार
- देर से
- Li
- पसंद
- सीमा
- जुड़ा हुआ
- थोड़ा
- जीना
- लाइव्स
- लंबा
- लंबे समय तक
- देखिए
- देख
- बंद
- लॉट
- बनाया गया
- प्रमुख
- बनाना
- बनाता है
- निर्माण
- बहुत
- मानचित्रण
- मार्जिन
- राज
- गणित
- गणितीय
- गणित
- मैट्रिक्स
- अधिकतम
- अर्थ
- उल्लेख किया
- तरीका
- तरीकों
- हो सकता है
- उपलब्धियां
- आदर्श
- मॉडल
- मॉड्यूलर
- पल
- महीने
- अधिक
- अधिकांश
- चाल
- विभिन्न
- रहस्यमय
- नाम
- आवश्यकता
- नेटवर्क
- नया
- नया साल
- अगला
- धारणा
- संख्या
- संख्या
- वस्तु
- वस्तुओं
- प्राप्त करने के
- of
- पुराना
- on
- ONE
- चल रहे
- खुला
- विपरीत
- मौलिक रूप से
- अन्य
- अन्य
- अपना
- काग़ज़
- समानांतर
- भाग
- विशेष
- विशेष रूप से
- भागों
- पथ
- पैटर्न उपयोग करें
- पेंसिल्वेनिया
- शायद
- परिप्रेक्ष्य
- पीटर
- PHP
- भौतिक विज्ञान
- प्लेटो
- प्लेटो डेटा इंटेलिजेंस
- प्लेटोडाटा
- प्ले
- सकारात्मक
- तैनात
- संभावित
- संभावित
- बिजली
- शक्तिशाली
- ठीक - ठीक
- सुंदर
- पिछला
- मुसीबत
- समस्याओं
- कार्यक्रम
- प्रगति
- परियोजना
- प्रमाण
- गुण
- संपत्ति
- साबित करना
- साबित
- प्रदान करता है
- प्रदान कर
- धक्का
- रखना
- डालता है
- क्वांटमगाज़ी
- मात्रा
- क्वांटम भौतिकी
- प्रश्न
- प्रशन
- बिना सोचे समझे
- दुर्लभ
- वास्तविक
- यथार्थवादी
- क्षेत्र
- कारण
- पहचान
- प्रतिबिंबित
- सम्बंधित
- संबंधों
- अपेक्षाकृत
- प्रतिनिधित्व
- अनुसंधान
- संकल्प
- संकल्प
- परिणाम
- परिणाम
- वापसी
- प्रकट
- धनी
- कठिन
- सड़क
- भूमिका
- जड़
- नियम
- कहा
- वही
- सांता
- संतुष्ट
- Search
- दूसरा
- सुरक्षित
- बीज
- लग रहा था
- लगता है
- सितंबर
- अनुक्रम
- कई
- सेट
- सेट
- सेटिंग्स
- सात
- कई
- चाहिए
- दिखाना
- पक्ष
- के बाद से
- एक
- आकार
- छोटा
- So
- समाधान
- हल
- कुछ
- कुछ
- अंतरिक्ष
- रिक्त स्थान
- विशेष
- सुर्ख़ियाँ
- चौकोर
- निरा
- प्रारंभ
- शुरू
- शुरुआत में
- राज्य
- कथन
- बयान
- राज्य
- कदम
- फिर भी
- कहानी
- सरल
- मजबूत
- संरचना
- अध्ययन
- का अध्ययन
- ऐसा
- की आपूर्ति
- सतह
- लेना
- लेता है
- तकनीक
- शर्तों
- परीक्षण
- कि
- RSI
- मैट्रिक्स
- लेकिन हाल ही
- उन
- सैद्धांतिक
- इन
- बात
- चीज़ें
- तीन
- यहाँ
- टाई
- सेवा मेरे
- भी
- टूलबॉक्स
- उपकरण
- ऊपर का
- की ओर
- <strong>उद्देश्य</strong>
- बदल गया
- प्रकार
- परम
- समझना
- समझ
- अप्रत्याशित
- खुलासा
- एकीकृत
- इकाई
- सार्वभौम
- ब्रम्हांड
- विश्वविद्यालय
- यूनिवर्सिटी ऑफ कैलिफोर्निया
- कैम्ब्रिज विश्वविद्यालय
- शिकागो विश्वविद्यालय
- us
- उपयोग
- मूल्य
- जरूरत है
- युद्ध
- मार्ग..
- तरीके
- में आपका स्वागत है
- क्या
- कौन कौन से
- जब
- पूरा का पूरा
- साथ में
- अंदर
- बिना
- काम
- काम किया
- विश्व
- होगा
- लिखा हुआ
- वर्ष
- साल
- प्राप्ति
- आप
- जेफिरनेट
- जीटा












