QuOne Lab, Phanous Research and Innovation Centre, Tehran, Iran
Érdekesnek találja ezt a cikket, vagy szeretne megvitatni? Scite vagy hagyjon megjegyzést a SciRate-en.
Absztrakt
Evolutions of local Hamiltonians in short times are expected to remain local and thus limited. In this paper, we validate this intuition by proving some limitations on short-time evolutions of local time-dependent Hamiltonians. We show that the distribution of the measurement output of short-time (at most logarithmic) evolutions of local Hamiltonians are $concentrated$ and satisfy an $textit{isoperimetric inequality}$. To showcase explicit applications of our results, we study the $M$$small{AX}$$C$$small{UT}$ problem and conclude that quantum annealing needs at least a run-time that scales logarithmically in the problem size to beat classical algorithms on $M$$small{AX}$$C$$small{UT}$. To establish our results, we also prove a Lieb-Robinson bound that works for time-dependent Hamiltonians which might be of independent interest.
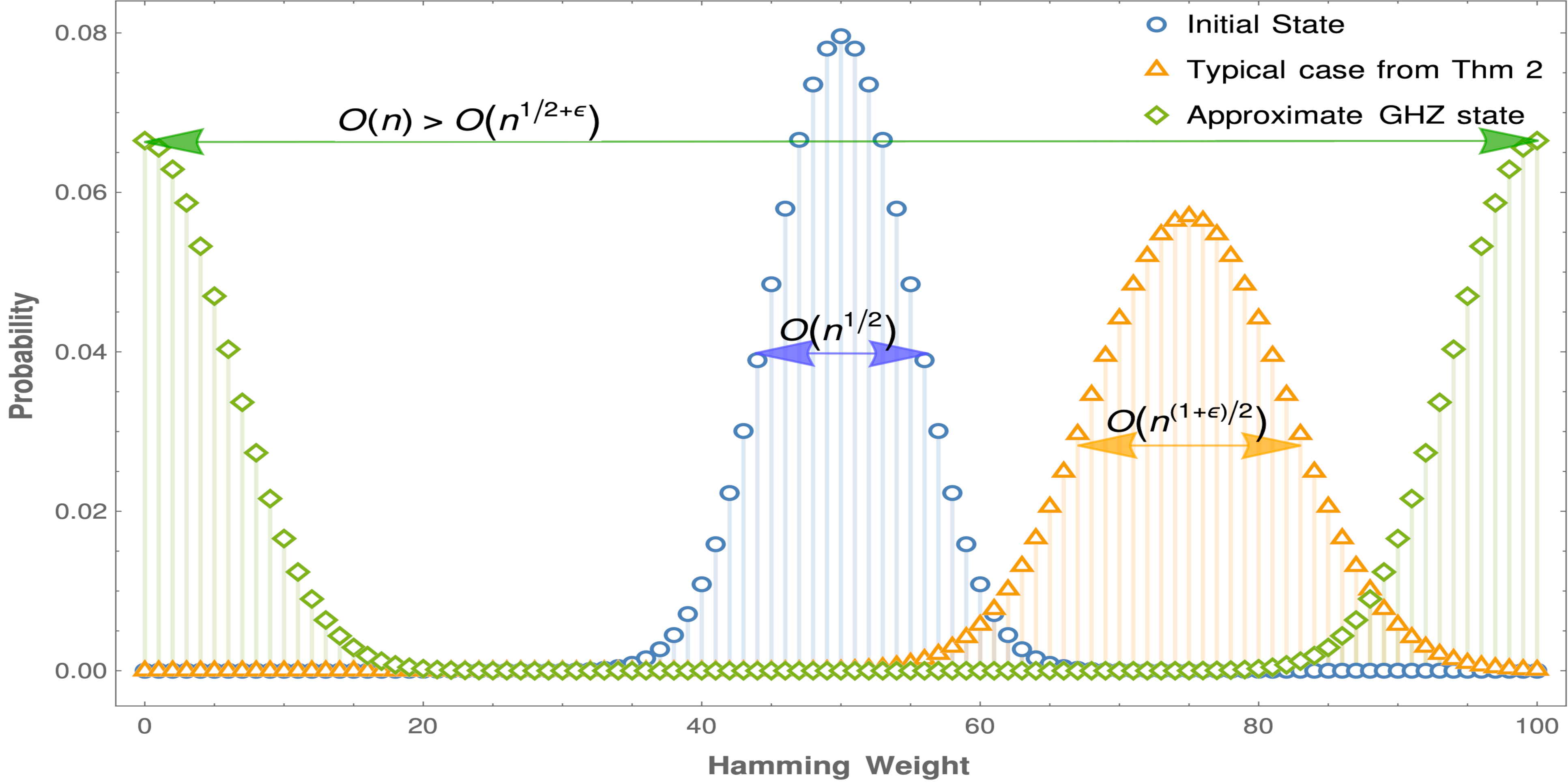
Featured image: This Illustration depicts the probability distribution of the Hamming weight of three different $n$-qubit states for $n=100$. The centered distribution in the middle (blue) is the typical distribution for a product initial state (e.g., $|+rangle^{otimes n}$). The distribution that is peaked just to the right (orange) represents the distribution after a short time evolution of the initial state described by Theorem 2 of the manuscript. The distribution that has two peaks on either side of the spectrum (green) is an approximation for the GHZ state. This shows that the GHZ state cannot be generated even approximately by a short-time quantum annealing.
Népszerű összefoglaló
► BibTeX adatok
► Referenciák
[1] T. Kadowaki and H. Nishimori. Quantum annealing in the transverse Ising model. Physical Review E 58, 5355–5363 (1998).
https:///doi.org/10.1103/PhysRevE.58.5355
[2] E. Farhi, J. Goldstone, S. Gutmann and M. Sipser. Quantum Computation by Adiabatic Evolution. arXiv:0001106 [quant-ph] (2000).
https:///doi.org/10.48550/arXiv.quant-ph/0001106
arXiv: 0001106
[3] T. Kato. On the adiabatic theorem of quantum mechanics. Journal of the Physical Society of Japan 5, 435–439 (1950).
https:///doi.org/10.1143/JPSJ.5.435
[4] M. Born and V. Fock. Beweis des adiabatensatzes. Zeitschrift für Physik 51, 165–180 (1928).
https:///doi.org/10.1007/BF01343193
[5] T. Albash and D. A. Lidar. Adiabatic quantum computation. Reviews of Modern Physics 90, 015002 (2018).
https:///doi.org/10.1103/RevModPhys.90.015002
[6] I. Hen and F. M. Spedalieri. Quantum Annealing for Constrained Optimization. Physical Review Applied 5, 034007 (2016).
https:///doi.org/10.1103/PhysRevApplied.5.034007
[7] S. Puri, C. K. Andersen, A. L. Grimsmo, and A. Blais. Quantum annealing with all-to-all connected nonlinear oscillators. Nature Communications 8, 15785 (2017).
https:///doi.org/10.1038/ncomms15785
[8] W. Lechner, P. Hauke, and P. Zoller. A quantum annealing architecture with all-to-all connectivity from local interactions. Science Advances 1, e1500838 (2015).
https:///doi.org/10.1126/sciadv.1500838
[9] S. Jiang, K. A. Britt, A. J. McCaskey, T. S. Humble, and S. Kais. Quantum Annealing for Prime Factorization. Scientific Reports 8, 17667 (2018).
https:///doi.org/10.1038/s41598-018-36058-z
[10] R. Y. Li, R. Di Felice, R. Rohs, and D. A. Lidar. Quantum annealing versus classical machine learning applied to a simplified computational biology problem. NPJ quantum information 4, 1–10 (2018).
https://doi.org/10.1038/s41534-018-0060-8
[11] L. Stella, G. E. Santoro, and E. Tosatti. Optimization by quantum annealing: Lessons from simple cases. Physical Review B 72, 014303 (2005).
https:///doi.org/10.1103/PhysRevB.72.014303
[12] O. Titiloye and A. Crispin. Quantum annealing of the graph coloring problem. Discrete Optimization 8, 376–384 (2011).
https:///doi.org/10.1016/j.disopt.2010.12.001
[13] A. Mott, J. Job, J.-R. Vlimant, D. Lidar, and M. Spiropulu. Solving a Higgs optimization problem with quantum annealing for machine learning. Nature 550, 375–379 (2017).
https:///doi.org/10.1038/nature24047
[14] K. L. Pudenz, T. Albash, and D. A Lidar. Quantum annealing correction for random Ising problems. Physical Review A 91, 042302 (2015).
https:///doi.org/10.1103/PhysRevA.91.042302
[15] A. Perdomo-Ortiz, N. Dickson, M. Drew-Brook, G. Rose, and A. Aspuru-Guzik. Finding low-energy conformations of lattice protein models by quantum annealing. Scientific reports 2, 571 (2012).
https:///doi.org/10.1038/srep00571
[16] K. L. Pudenz, T. Albash, and D. A Lidar. Error-corrected quantum annealing with hundreds of qubits. Nature communications 5, 1–10 (2014).
https:///doi.org/10.1038/ncomms4243
[17] R. Martoňák, G. E. Santoro, and E. Tosatti. Quantum annealing of the traveling-salesman problem. Physical Review E 70, 057701 (2004).
https:///doi.org/10.1103/PhysRevE.70.057701
[18] S. H. Adachi and M. P. Henderson. Application of quantum annealing to training of deep neural networks. arXiv:1510.06356 [quant-ph] (2015).
https:///doi.org/10.48550/arXiv.1510.06356
arXiv: 1510.06356
[19] M. W Johnson, et al. Quantum annealing with manufactured spins. Nature 473, 194–198 (2011).
https:///doi.org/10.1038/nature10012
[20] S. Boixo, T. Albash, F. M. Spedalieri, N. Chancellor, and D. A. Lidar. Experimental signature of programmable quantum annealing. Nature communications 4, 1–8 (2013).
https:///doi.org/10.1038/ncomms3067
[21] A. D. King, et al. Coherent quantum annealing in a programmable 2000-qubit Ising chain. arXiv:2202.05847 [quant-ph] (2022).
https:///doi.org/10.48550/arXiv.2202.05847
arXiv: 2202.05847
[22] B. Foxen, et al. Demonstrating a Continuous Set of Two-qubit Gates for Near-term Quantum Algorithms. Physical Review Letters 125, 120504 (2020).
https:///doi.org/10.1103/PhysRevLett.125.120504
[23] K. Wright, et al. Benchmarking an 11-qubit quantum computer. Nature communications 10, 1–6 (2019).
https://doi.org/10.1038/s41467-019-13534-2
[24] E. J. Crosson and D. A. Lidar. Prospects for quantum enhancement with diabatic quantum annealing. Nature Reviews Physics 3, 466–489 (2021).
https://doi.org/10.1038/s42254-021-00313-6
[25] E. Farhi, J. Goldstone, and S. Gutmann. A Quantum Approximate Optimization Algorithm. arXiv:1411.4028 [quant-ph] (2014).
https:///doi.org/10.48550/arXiv.1411.4028
arXiv: 1411.4028
[26] E. Farhi, D. Gamarnik, and S. Gutmann. The Quantum Approximate Optimization Algorithm Needs to See the Whole Graph: Worst Case Examples. arXiv:2005.08747 [quant-ph] (2020).
https:///doi.org/10.48550/arXiv.2005.08747
arXiv: 2005.08747
[27] E. Farhi, D. Gamarnik, and S. Gutmann. The Quantum Approximate Optimization Algorithm Needs to See the Whole Graph: A Typical Case. arXiv:2004.09002 [quant-ph] (2020).
https:///doi.org/10.48550/arXiv.2004.09002
arXiv: 2004.09002
[28] S. Bravyi, A. Kliesch, R. Koenig, and E. Tang. Obstacles to Variational Quantum Optimization from Symmetry Protection. Physical Review Letters 125, 260505 (2020).
https:///doi.org/10.1103/PhysRevLett.125.260505
[29] S. Bravyi, D. Gosset, and R. Movassagh. Classical algorithms for quantum mean values. Nature Physics 17, 337–341 (2021).
https://doi.org/10.1038/s41567-020-01109-8
[30] S. Bravyi, A. Kliesch, R. Koenig, and E. Tang. Hybrid quantum-classical algorithms for approximate graph coloring. Quantum 6, 678 (2022).
https://doi.org/10.22331/q-2022-03-30-678
[31] L. Eldar and A. W. Harrow. Local Hamiltonians Whose Ground States are Hard to Approximate. In 2017 IEEE 58th Annual Symposium on Foundations of Computer Science (FOCS), 427–438 (2017).
https:///doi.org/10.1109/FOCS.2017.46
[32] L. T. Brady, C. L. Baldwin, A. Bapat, Y. Kharkov, and A. V. Gorshkov. Optimal Protocols in Quantum Annealing and Quantum Approximate Optimization Algorithm Problems. Physical Review Letters 126, 070505 (2021).
https:///doi.org/10.1103/PhysRevLett.126.070505
[33] L. T. Brady, L. Kocia, P. Bienias, A. Bapat, Y. Kharkov, and A. V. Gorshkov. Behavior of Analog Quantum Algorithms. arXiv:2107.01218 [quant-ph] (2021).
https:///doi.org/10.48550/arXiv.2107.01218
arXiv: 2107.01218
[34] L. C. Venuti, D. D’Alessandro, and D. A. Lidar. Optimal Control for Quantum Optimization of Closed and Open Systems. Physical Review Applied 16, 054023 (2021).
https:///doi.org/10.1103/PhysRevApplied.16.054023
[35] A. M. Childs, Y. Su, M. C. Tran, N. Wiebe, and S. Zhu. Theory of Trotter Error with Commutator Scaling. Physical Review X 11, 011020 (2021).
https:///doi.org/10.1103/PhysRevX.11.011020
[36] B. Nachtergaele, Y. Ogata, and R. Sims. Propagation of correlations in quantum lattice systems. Journal of Statistical Physics 124, 1–13 (2006).
https://doi.org/10.1007/s10955-006-9143-6
[37] B. Nachtergaele and R. Sims. Lieb-Robinson bounds in quantum many-body physics. Contemporary Mathematics 529, 141–176 (2010).
https:///doi.org/10.1090/conm/529/10429
[38] S. Bravyi, M. B. Hastings, and F. Verstraete. Lieb-robinson bounds and the generation of correlations and topological quantum order. Physical Review Letters 97, 050401 (2006).
https:///doi.org/10.1103/PhysRevLett.97.050401
[39] C.-F. Chen and A. Lucas. Operator growth bounds from graph theory. Communications in Mathematical Physics 385, pages1273–1323 (2021).
https://doi.org/10.1007/s00220-021-04151-6
[40] E.H. Lieb and D.W. Robinson. The finite group velocity of quantum spin systems. Communications in Mathematical Physics 28, 251–257 (1972).
https:///doi.org/10.1007/BF01645779
[41] J. Haah, M. B. Hastings, R. Kothari, and G. H. Low. Quantum algorithm for simulating real time evolution of lattice Hamiltonians. 2018 IEEE 59th Annual Symposium on Foundations of Computer Science (FOCS), 350–360 (2018).
https:///doi.org/10.1109/FOCS.2018.00041
[42] A. Lubotzky, R. Phillips, and P. Sarnak. Ramanujan graphs. Combinatorica 8, 261–277 (1988).
https:///doi.org/10.1007/BF02126799
[43] B. Mohar. Isoperimetric numbers of graphs. Journal of Combinatorial Theory, Series B 47, 274–291 (1989).
https://doi.org/10.1016/0095-8956(89)90029-4
[44] A. W. Marcus, D. A. Spielman, and N. Srivastava. Interlacing Families IV: Bipartite Ramanujan Graphs of All Sizes. In 2015 IEEE 56th Annual Symposium on Foundations of Computer Science (FOCS), 1358–1377 (2015).
https:///doi.org/10.1109/FOCS.2015.87
[45] A. W. Marcus, D. A. Spielman, and N. Srivastava. Interlacing Families IV: Bipartite Ramanujan Graphs of All Sizes. SIAM Journal on Computing 47, 2488–2509 (2018).
https:///doi.org/10.1137/16M106176X
[46] C. Hall, D. Puder, and W. F. Sawin. Ramanujan coverings of graphs. Advances in Mathematics 323, 367–410 (2018).
https:///doi.org/10.1016/j.aim.2017.10.042
[47] M. X. Goemans and D. P. Williamson. Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming. Journal of the ACM 42, 1115–1145 (1995).
https:///doi.org/10.1145/227683.227684
[48] R. D. Somma, D. Nagaj, and M. Kieferová. Quantum Speedup by Quantum Annealing. Physical Review Letters 109, 050501 (2012).
https:///doi.org/10.1103/PhysRevLett.109.050501
[49] M. B. Hastings. The Power of Adiabatic Quantum Computation with No Sign Problem. Quantum 5, 597 (2021).
https://doi.org/10.22331/q-2021-12-06-597
[50] A. Gilyén, M. B. Hastings, and U. Vazirani. (Sub)Exponential advantage of adiabatic Quantum computation with no sign problem. In Proceedings of the Annual ACM Symposium on Theory of Computing (STOC), 1357–1369 (2021).
https:///doi.org/10.1145/3406325.3451060
[51] R. Bhatia. Matrix analysis. Graduate Texts in Mathematics. Springer New York (1996).
https://doi.org/10.1007/978-1-4612-0653-8
[52] R. Bhatia. Positive definite matrices. Princeton University Press, (2007).
https:///doi.org/10.1515/9781400827787
[53] B.D. McKay, N.C. Wormald, and B. Wysocka. Short Cycles in Random Regular Graphs. The Electronic Journal of Combinatorics 11, 1–12 (2004).
https:///doi.org/10.37236/1819
[54] F. Kardoš, D. Král, and J. Volec. Maximum edge-cuts in cubic graphs with large girth and in random cubic graphs. Random Structures & Algorithms 41, 506–520 (2012).
https:///doi.org/10.1002/rsa.20471
[55] D. Coppersmith, D. Gamarnik, M.T. Hajiaghayi, and G.B. Sorkin. Random MAX SAT, random MAX CUT, and their phase transitions. Random Structures and Algorithms 24, 502–545 (2004).
https:///doi.org/10.1002/rsa.20015
[56] A. Dembo, A. Montanari, and S. Sen. Extremal cuts of sparse random graphs. Annals of Probability 45, 1190–1217 (2017).
https:///doi.org/10.1214/15-AOP1084
Idézi
[1] Giacomo De Palma, Milad Marvian, Cambyse Rouzé és Daniel Stilck França, „Limitations of variational quantum algorithms: a quantum optimal transport approach”, arXiv: 2204.03455.
A fenti idézetek innen származnak SAO/NASA HIRDETÉSEK (utolsó sikeres frissítés: 2022-07-19 03:10:09). Előfordulhat, hogy a lista hiányos, mivel nem minden kiadó ad megfelelő és teljes hivatkozási adatokat.
On Crossref által idézett szolgáltatás művekre hivatkozó adat nem található (utolsó próbálkozás 2022-07-19 03:10:07).
Ez a tanulmány a Quantumban jelent meg Creative Commons Nevezd meg 4.0 International (CC BY 4.0) engedély. A szerzői jog az eredeti szerzői jog tulajdonosainál marad, például a szerzőknél vagy intézményeiknél.