Una nuova prova distingue le "forme modulari" misteriose e potenti

In una nuova dimostrazione, un oggetto matematico a lungo trascurato ha finalmente ottenuto il suo momento sotto i riflettori.

A prima vista, le forme modulari - funzioni le cui abbondanti simmetrie hanno incuriosito i matematici per secoli - sembrano aver raccolto un'attenzione più che sufficiente. Sorgono in tutti i tipi di problemi: sono stati un ingrediente chiave nella dimostrazione del 1994 di Andrew Wiles dell'ultimo teorema di Fermat, che ha risolto una delle più grandi questioni aperte nella teoria dei numeri. Svolgono un ruolo centrale nella Programma Langland, uno sforzo continuo per sviluppare "una grande teoria unificata della matematica". Sono stati persino usati per studiare modelli nella teoria delle stringhe e nella fisica quantistica.

Ma le forme modulari che nascono in questi contesti sono di un tipo speciale. Le forme modulari cosiddette "congruenza" vantano una struttura aggiuntiva che le rende più facili da studiare. Ma le forme modulari di "non congruenza" più generali superano di gran lunga le loro controparti amichevoli di congruenza. "Se prendi una forma modulare casuale, con probabilità 1 è non congruenza", ha detto Cameron Franco, un matematico della McMaster University in Canada. “A meno che tu non abbia davvero una buona ragione per incontrare una forma modulare di congruenza, non te lo aspetteresti. Sono molto rari.

Eppure i matematici sanno molto poco delle forme modulari di non congruenza, nonostante la loro ubiquità. "Sono completamente misteriosi", ha detto Antonio Scholl, un matematico dell'Università di Cambridge. Non solo è difficile fare affermazioni onnicomprensive su una classe così generale di funzioni, ma gli strumenti sviluppati per studiare le forme modulari falliscono nel caso di non congruenza. Ciò ha lasciato i matematici incerti su ciò che avrebbero dovuto provare a dimostrare.

Tuttavia, una delle principali congetture sulle forme modulari non congruenti è emersa da tempo: un cartello segnaletico solitario e instabile nel deserto.

Nel 1968, i matematici Oliver Atkin e Peter Swinnerton-Dyer notarono che le forme modulari di non congruenza sembravano avere una proprietà particolarmente evidente che le distingueva dalle forme modulari di congruenza. Che ci dovrebbe essere un modo così sfacciato per distinguere i due "è davvero sorprendente", ha detto Geoffrey Mason, un matematico dell'Università della California, Santa Cruz. Le forme modulari di congruenza e non congruenza sono molto diverse, perché le forme modulari di non congruenza mancano di simmetrie che hanno le forme modulari di congruenza. Ma queste differenze, sebbene importanti, possono essere sottili e difficili da rilevare.

Qui, all'improvviso, c'era la netta evidenza di queste differenze, rese evidenti.

L'osservazione di Atkin e Swinnerton-Dyer divenne in seguito nota come la congettura dei "denominatori illimitati". Se vero, consentirebbe ai matematici di assicurarsi il loro primo punto d'appoggio nel regno in gran parte inesplorato degli oggetti non congruenti. E fornendo un modo semplice per riconoscere a quale classe appartenesse una data forma modulare, la congettura potrebbe anche collocare un importante programma di fisica teorica — finalizzato alla comprensione dei modelli di interazione delle particelle chiamate teorie di campo conformi — su un terreno matematico più solido.

Ma per più di 50 anni nessuno ha potuto provarlo. Infine, alla fine del 2021, un trio di matematici è riuscito. La loro prova sembrava provenire dal nulla, impiegando tecniche che nessuno si aspettava di vedere in quest'area di studio. Matematici e fisici stanno ora iniziando a esplorare le conseguenze di quel lavoro.

Simmetria e struttura

Le forme modulari non congruenti non erano sempre relegate ai margini.

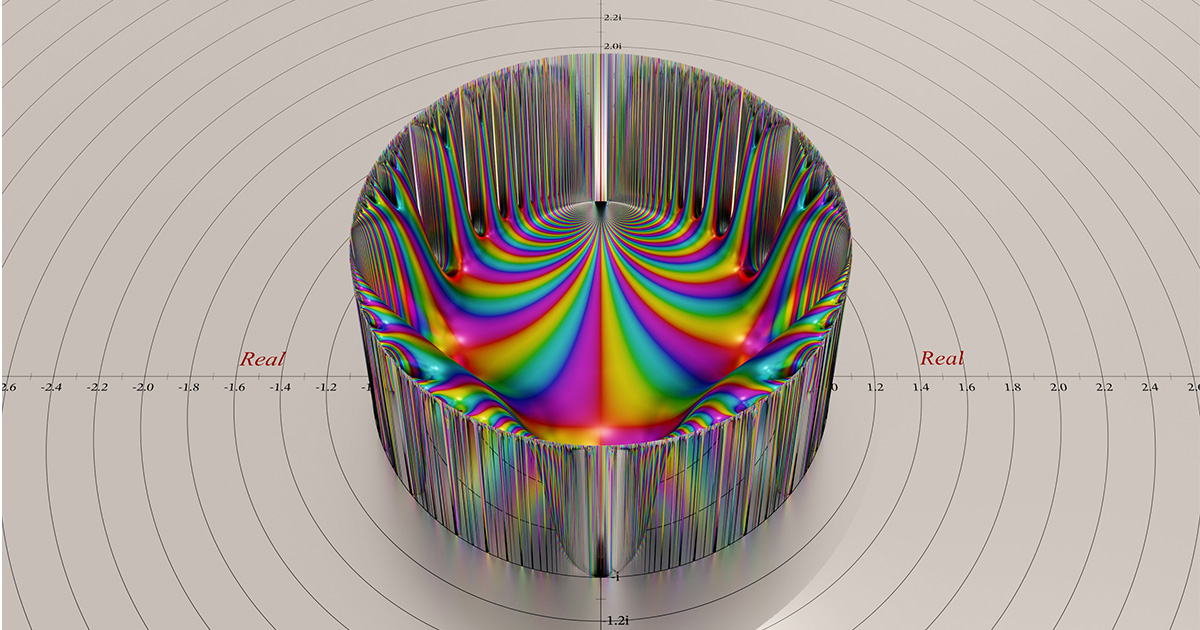
Nel diciannovesimo secolo, i matematici stavano appena iniziando a sviluppare una teoria delle forme modulari. Questo era il nome dato a un particolare tipo di funzione altamente simmetrica, che vive in un dominio noto come la metà superiore del piano complesso.

Il piano complesso è un modo per rappresentare graficamente numeri complessi, che hanno due parti: reale e immaginaria. Una forma modulare prende come input numeri complessi la cui parte immaginaria è positiva, corrispondente alla metà superiore del piano. (Il semipiano superiore può essere facilmente mappato all'interno di un disco unitario; le forme modulari sono spesso rappresentate utilizzando questa mappatura.)

Le numerose simmetrie delle forme modulari sono definite in termini di raccolte speciali, o "gruppi", di matrici 2 per 2: matrici quadrate di quattro numeri. Nelle forme modulari, quei quattro numeri sono sempre numeri interi. Fondamentalmente, un numero associato alla matrice che determina alcune delle sue proprietà, chiamato determinante, deve essere 1.

Esistono infiniti insiemi di tali matrici. In alcuni gruppi, le matrici possono essere descritte da regole relativamente semplici. Ad esempio, in tutte le matrici, le voci in alto a destra e in basso a sinistra potrebbero essere pari, mentre le altre due voci sono dispari. O forse le voci in alto a destra e in basso a sinistra sono divisibili per 11, mentre le altre due voci sono entrambe 1 più di un multiplo di 11.

I gruppi che possono essere definiti da questo tipo di relazioni - e le forme modulari associate a tali gruppi - sono quelli di congruenza molto studiati.

Ma sono come aghi in un pagliaio: la maggior parte delle raccolte di matrici 2 per 2 non possono essere caratterizzate da belle regole in questo modo, rendendo loro e le loro forme modulari associate non congruenti.

Non è stato fino alla fine degli anni '1930 - intorno all'inizio della seconda guerra mondiale - che lo studio delle forme modulari di congruenza ha iniziato a eclissare lo studio di quelle di non congruenza. Fu allora che il matematico tedesco Erich Hecke sviluppò una cassetta degli attrezzi che gli avrebbe permesso di definire molte proprietà delle forme modulari e di associarle ad altri importanti oggetti matematici.

I metodi di Hecke funzionavano solo per i gruppi di congruenza e le loro forme modulari. I gruppi di non congruenza mancavano della struttura extra che rendeva efficace la cassetta degli attrezzi di Hecke. "Questa cosa che hai nel mondo della congruenza esce dalla porta quando ti sposti nel mondo della non congruenza", ha detto Franc.

E così sembrava che le forme modulari non congruenti fossero destinate a essere sempre trascurate. Questo non vuol dire che non avessero alcun tipo di struttura speciale propria, in agguato appena sotto la superficie. Come scrisse una volta il collaboratore di Swinnerton-Dyer, Bryan Birch, "Sebbene la struttura sia più misteriosa, sembra essere quasi altrettanto ricca". Ma quando si trattava di accedere a quella struttura, i matematici erano perplessi. Non sapevano nemmeno da dove cominciare.

Entrano Atkin e Swinnerton-Dyer.

Un criterio ordinato

I due matematici volevano saperne di più sulle forme modulari di non congruenza e sui segreti che potevano nascondere.

"Questo è sempre il modo in cui la matematica progredisce", ha detto Winnie Li, un matematico della Pennsylvania State University. “Studi cose con proprietà molto speciali e più struttura. Poi vai a generalizzarlo, per cercare di capire quali proprietà si trasferiscono e quali no”.

Per studiare una data forma modulare, i matematici spesso la rappresentano come una somma infinita chiamata espansione q (un tipo speciale di serie di potenze), quindi analizzano i coefficienti di tale espansione. Era già noto che se una data forma modulare è congruenza, allora i coefficienti hanno denominatori che non diventano mai maggiori di un valore fisso.

Negli anni '1960, Atkin e Swinnerton-Dyer calcolarono le q-espansioni per partiture e partiture di forme modulari. Mentre lo facevano, notarono che se una forma modulare era non congruente, i denominatori nella sua sequenza associata continuavano a crescere senza limiti. "Potrebbero effettivamente dire qualcosa su queste misteriose forme di non congruenza", ha detto Yunqing Tang, un matematico dell'Università della California, Berkeley.

Potrebbe davvero essere così facile distinguere i due tipi di forme modulari?

I matematici menzionarono la loro osservazione in una conferenza in California nel 1968, suggerendo che i denominatori illimitati potrebbero essere un segno distintivo universale delle forme modulari non congruenti. La congettura è stata "molto sorprendente", ha detto John Voight, matematico al Dartmouth College. "Ci fornisce un criterio ordinato per decidere se una forma modulare appartiene o meno a un gruppo di congruenza" - una cartina di tornasole molto conveniente per i teorici dei numeri da avere a loro disposizione e qualcosa che in altri contesti potrebbe essere difficile da rilevare.

"È quasi troppo bello per essere vero", ha aggiunto. "Non ci si aspetta davvero quel tipo di miracolo."

In effetti, nessuno potrebbe dimostrare la congettura dei denominatori illimitati. Li e una manciata di altri lo erano in grado di mostrare era vero per famiglie specifiche di forme modulari non congruenti, ma i matematici non avevano idea di come affrontare l'enunciato generale.

Poi, nel settembre 2021, Tang, insieme a Franco Calegari dell'Università di Chicago e Vesselin Dimitrov dell'Institute for Advanced Study, ha pubblicato una prova di 50 pagine. "È stato fantastico e davvero inaspettato", ha detto Franc. "Sembrava che la comunità non avesse avuto alcuna idea su come affrontare questo problema".

Gli autori sperano che il loro articolo sia il primo passo verso lo sviluppo di quel cartello nel deserto in una vera e propria rete stradale. "Diamo il nostro modesto contributo a questa parte della teoria dei numeri fornendo la risposta alla sua domanda più semplice", ha detto Dimitrov.

Torna ai vecchi modi

Calegari, Dimitrov e Tang non si sono proposti di risolvere la congettura dei denominatori illimitati. Alla fine del 2019, speravano di dimostrare che un certo numero (un valore analogo alla funzione zeta di Riemann) era irrazionale e che, come la radice quadrata di 2, non può essere scritto come frazione. (Il loro obiettivo finale è dimostrare che questo numero e altri simili sono trascendentali, il che significa che, come con i numeri π ed e, non possono essere scritti come la soluzione di un'equazione polinomiale con coefficienti interi.)

A prima vista, questo problema è del tutto estraneo. Ma il 1° gennaio 2021, Dimitrov ha telefonato al nuovo anno con un'e-mail agli altri in cui descriveva "un pio desiderio": forse le tecniche che avevano sviluppato nell'anno precedente potevano essere riproposte per dimostrare la congettura dei denominatori illimitati.

Ci hanno provato. Entro sette mesi, hanno avuto la loro prova.

In primo luogo, hanno considerato due spazi: lo spazio di tutte le forme modulari con denominatori limitati e lo spazio di tutte le forme modulari di congruenza. Secondo la congettura dei denominatori illimitati, questi due spazi dovrebbero essere identici. Poiché gli spazi soddisfacevano determinate proprietà, i matematici dovevano solo dimostrare che avevano la stessa dimensione. Ciò implicherebbe automaticamente la loro equivalenza.

Calegari, Dimitrov e Tang hanno potuto calcolare con relativa facilità la dimensione del secondo spazio, ottenendo una sorta di conteggio approssimativo delle forme modulari di congruenza. Ma è stato molto difficile ottenere una stima delle dimensioni del primo spazio. Hanno dovuto combinare molte tecniche diverse, comprese quelle della teoria dei numeri trascendentale.

Usando questi metodi, hanno dimostrato che lo spazio delle forme modulari con denominatori limitati può essere al massimo di una certa dimensione. Quella dimensione massima era un po' più grande della dimensione dello spazio delle forme modulari di congruenza. Tuttavia, questo passaggio si è rivelato "essere davvero il cuore della prova", ha detto Jean-Benoît Bost, matematico all'Università Paris-Saclay. "Ci vuole molta forza d'animo per farlo." (Calegari, Dimitrov e Tang hanno dimostrato questo limite alla dimensione dello spazio in una manciata di modi diversi, dando potenzialmente alle loro tecniche applicazioni molto più ampie.)

"È molto, molto classica, bella matematica, con un sapore del 19° secolo", ha detto Javier Fresan, matematico all'École Polytechnique in Francia.

Il trio doveva quindi colmare il divario tra i due spazi. In questo modo si stabilirebbe che qualsiasi forma modulare con denominatori limitati doveva essere congruenza.

Quindi hanno assunto l'opposto: che esiste una forma modulare di non congruenza con denominatori limitati. Per definizione vivrebbe nel vuoto che Calegari, Dimitrov e Tang stavano cercando di colmare. I tre hanno quindi dimostrato che l'esistenza di questa forma modulare di non congruenza implicava automaticamente l'esistenza di molte altre forme modulari di non congruenza con denominatori limitati. Era come se da quel singolo seme fosse cresciuta un'intera foresta.

Ma avevano già stabilito la dimensione massima del divario - ed era troppo piccolo per adattarsi a tante forme di non congruenza.

Il che significava che nemmeno una di queste forme poteva esistere. Avevano dimostrato la congettura vecchia di decenni di Atkin e Swinnerton-Dyer.

I matematici trovano le tecniche utilizzate nel lavoro ancora più intriganti del risultato stesso. "Queste idee non sono mai state utilizzate prima nello studio dell'aritmetica delle forme modulari", ha detto Scholl.

Come spiega Voight, sebbene lo studio delle forme modulari sia iniziato come parte del campo dell'analisi complessa, il lavoro attuale è stato di competenza della teoria dei numeri e della geometria algebrica. Il nuovo documento, ha detto, segna un ritorno all'analisi complessa: "È una prospettiva piacevolmente vecchia".

Una ricerca di nuove teorie

I matematici non sono gli unici entusiasti della congettura dei denominatori illimitati. Fa anche la sua comparsa nella fisica teorica.

Negli anni '1970, un'altra storia si stava svolgendo parallelamente a quella iniziata da Atkin e Swinnerton-Dyer. I matematici avevano notato una strana connessione tra un oggetto chiamato il gruppo di mostri e una forma modulare chiamata il j-funzione. I coefficienti di j-la funzione rifletteva precisamente alcune proprietà del gruppo dei mostri.

Ricerche successive hanno rivelato che questa connessione era dovuta al fatto che sia il gruppo che la forma modulare erano correlati a un importante modello di interazione tra particelle chiamato teoria del campo conforme bidimensionale.

Ma la teoria del campo conforme che collegava il gruppo dei mostri al... jLa funzione era solo un esempio di un numero infinito di teorie di campo conformi. E mentre queste teorie non descrivono l'universo in cui viviamo, la loro comprensione può fornire nuove intuizioni su come potrebbero comportarsi teorie quantistiche di campo più realistiche.

E così i fisici hanno continuato a studiare le teorie di campo conformi osservando le loro forme modulari associate. (In questo contesto, i fisici usano una nozione più generale di forma modulare, chiamata forma modulare a valori vettoriali.)

Per capire cosa sta succedendo con una particolare teoria di campo conforme, devi dimostrare che la sua forma modulare è congruenza, ha detto Michele Tuite, matematico e fisico teorico presso l'Università di Galway in Irlanda. Puoi quindi iniziare a descrivere teorie di campo conformi e persino scoprirne di nuove che non sapevi cercare. Ciò è particolarmente cruciale per uno sforzo in corso per classificare tutte le teorie di campo conformi, un progetto che i fisici hanno soprannominato bootstrap modulare.

"Una volta che sai che è una forma modulare di congruenza, che ti consente di fare enormi passi avanti in questo programma", ha detto Mason.

I fisici hanno sviluppato una struttura che consente loro di assumere questa proprietà di congruenza per le forme modulari che stanno studiando. Ma non è la stessa cosa che avere una dimostrazione matematica rigorosa - e mentre altri matematici sono stati in grado di farlo in seguito fornire tale prova, il loro argomento ha funzionato solo in determinate impostazioni. Ha comportato anche "un percorso molto tortuoso e contorto" verso la congruenza, secondo Mason, sebbene abbia anche sottolineato che questo percorso contorto ha prodotto importanti intuizioni.

La dimostrazione di Calegari, Dimitrov e Tang della congettura dei denominatori illimitati taglia tutto questo. Questo perché, come risulta, le forme modulari associate alle teorie di campo conformi hanno sempre coefficienti interi. Per definizione, i numeri interi hanno denominatore 1, il che significa che i loro denominatori sono sempre limitati. E poiché la congettura dei denominatori illimitati afferma che i denominatori limitati sono associati solo a forme modulari di congruenza, non è più necessario fare ipotesi. "Non hai nemmeno bisogno di sapere nulla di [teorie di campo conformi]", ha detto Tang. La nuova dimostrazione fornisce automaticamente la congruenza per tutti questi casi, gratuitamente.

"È qualcosa che è stato nell'aria per decenni", ha detto Bost. Ora è finalmente risolto.

"È davvero un miracolo", ha detto Mason. "Questo deriva miracolosamente dal fatto che queste sequenze sono numeri interi."

Ha già iniziato ad applicare il risultato nel suo lavoro. "Sin dal giorno in cui è apparso quel giornale, l'ho usato", ha detto. “Fornisce una scorciatoia molto gradita ai risultati che voglio risolvere. ... Sta tagliando un'enorme quantità di lavoro potenziale che non riuscivo a vedere la mia strada.

Mette anche il programma bootstrap modulare e altri risultati su basi matematiche più solide. "Questo consentirà ai matematici di riprovare i risultati [precedenti] o di crederci", ha detto Mason.

"Penso che avrà davvero un impatto, specialmente dal punto di vista della matematica, solo per legare davvero le cose, per capire esattamente cosa sta succedendo", ha detto Tuite.

Trascendenza Matematica

Nell'anno da quando hanno pubblicato la loro prova, Calegari, Dimitrov e Tang hanno continuato la loro collaborazione. Ora sono tornati ai tipi di problemi nella teoria dei numeri trascendentali che originariamente avevano suscitato il loro interesse per la congettura. "Stiamo cercando di finire quello che abbiamo iniziato", ha detto Tang. In effetti, hanno già usato le loro tecniche per dimostrare che diversi numeri di interesse sono irrazionali.

"Stanno davvero spingendo il [metodo] al limite", ha detto Fresán. "Sono davvero molto entusiasta di questo."

Questi metodi potrebbero anche essere applicabili ad altri problemi di teoria dei numeri.

Tecniche a parte, la risoluzione della congettura dei denominatori illimitati segna una delle prime grandi pietre miliari nello sforzo di ottenere una migliore comprensione delle forme modulari di non congruenza. "Questo è un risultato straordinario, che possiamo fare dei progressi sulle forme di non congruenza in questo modo", ha detto Franc. "Sono entusiasta per i prossimi 10, 20 anni, per vedere cosa succede."

Li, Voight e altri stanno già iniziando a cercare modelli nei tipi di numeri che compaiono nei denominatori di queste misteriose forme modulari. Sperano che così facendo possano trovare indizi di una struttura più profonda.

"Questa congettura sui denominatori illimitati è stata solo l'inizio", ha detto Li.