Nytt bevis skiller mystiske og kraftige "modulære former"

I et nytt bevis har et lenge forsømt matematisk objekt endelig fått sitt øyeblikk i søkelyset.

Ved første øyekast ser det ut til at modulære former - funksjoner hvis rikelige symmetrier har fascinert matematikere i århundrer - har fått mer enn nok oppmerksomhet. De dukker opp i alle slags problemer: De var en nøkkelingrediens i Andrew Wiles' bevis fra 1994 på Fermats siste teorem, som løste et av de største åpne spørsmålene innen tallteori. De spiller en sentral rolle i Langlands program, et pågående forsøk på å utvikle «en storslått, enhetlig teori om matematikk». De har til og med blitt brukt til å studere modeller innen strengteori og kvantefysikk.

Men de modulære formene som oppstår i disse sammenhengene er av en spesiell type. Såkalte "kongruens" modulære former har ekstra struktur som gjør dem lettere å studere. Men mer generelle "ikke-kongruens" modulære former overgår i stor grad deres vennlige kongruens-motstykker. "Hvis du tar en tilfeldig modulær form, med sannsynlighet 1 er det ikke-kongruens," sa Cameron Franc, en matematiker ved McMaster University i Canada. "Med mindre du har en virkelig god grunn til å møte en kongruensmodulær form, ville du ikke forvente det. De er veldig sjeldne."

Og likevel vet matematikere veldig lite om ikke-kongruens modulære former, til tross for deres allestedsnærværende. "De er helt mystiske," sa Anthony Scholl, en matematiker ved University of Cambridge. Ikke bare er det vanskelig å komme med altomfattende utsagn om en slik generell klasse av funksjoner, men verktøyene som er utviklet for å studere modulære former, bryter sammen i tilfellet med ikke-kongruens. Dette har gjort matematikere usikre på hva de til og med skal prøve å bevise.

En stor formodning om ikke-kongruens modulære former har imidlertid lenge skilt seg ut: en enslig, ustø skilt i ørkenen.

I 1968 la matematikerne Oliver Atkin og Peter Swinnerton-Dyer merke til at ikke-kongruens-modulære former så ut til å ha en spesielt iøynefallende egenskap som skilte dem fra kongruens-modulære former. At det skulle være en så åpenbar måte å skille de to fra hverandre "er egentlig ganske forbløffende," sa Geoffrey Mason, en matematiker ved University of California, Santa Cruz. Kongruens og ikke-kongruens modulære former er veldig forskjellige, fordi ikke-kongruens modulære former mangler symmetrier som kongruens modulære former har. Men disse forskjellene, selv om de er viktige, kan være subtile og vanskelige å oppdage.

Her ble det plutselig tydelige bevis på disse forskjellene.

Atkin og Swinnerton-Dyers observasjon ble senere kjent som antagelsen om "ubegrensede nevnere". Hvis det er sant, vil det tillate matematikere å sikre sitt første fotfeste i det stort sett uutforskede riket av ikke-kongruensobjekter. Og ved å gi en enkel måte å gjenkjenne hvilken klasse en gitt modulær form tilhørte, kunne formodningen også sette et større program i teoretisk fysikk - et rettet mot å forstå modeller for partikkelinteraksjoner kalt konforme feltteorier - på fastere matematisk grunn.

Men i mer enn 50 år var det ingen som kunne bevise det. Endelig, på slutten av 2021, en trio av matematikere lyktes. Beviset deres så ut til å komme ut av ingensteds, ved å bruke teknikker ingen hadde forventet å se i dette studieområdet. Matematikere og fysikere begynner nå å utforske konsekvensene av dette arbeidet.

Symmetri og struktur

Ikke-kongruens modulære former ble ikke alltid henvist til marginene.

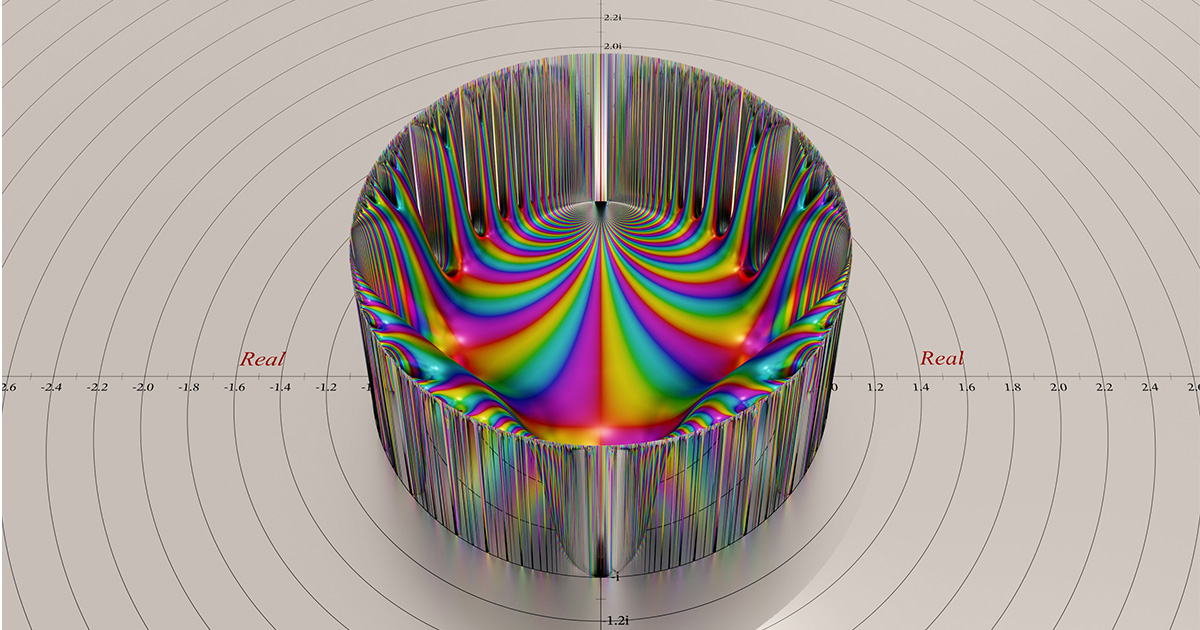
På 19-tallet begynte matematikere akkurat å utvikle en teori om modulære former. Dette var navnet gitt til en spesiell type svært symmetrisk funksjon - en som lever i et domene kjent som den øvre halvdelen av det komplekse planet.

Det komplekse planet er en måte å tegne komplekse tall på, som har to deler: reelle og imaginære. En modulær form tar som inngang komplekse tall hvis imaginære del er positiv, tilsvarende den øvre halvdelen av planet. (Det øvre halvplanet kan enkelt kartlegges til det indre av en enhetsdisk; modulære former er ofte avbildet ved hjelp av denne kartleggingen.)

De mange symmetriene til modulære former er definert i form av spesielle samlinger, eller "grupper", av 2-av-2 matriser - firkantede matriser med fire tall. I modulære former er disse fire tallene alltid heltall. Avgjørende må et tall assosiert med matrisen som bestemmer noen av dens egenskaper - kalt determinanten - være 1.

Det finnes uendelig mange slike sett med matriser. I noen grupper kan matrisene beskrives med relativt enkle regler. For eksempel, i alle matrisene, kan oppføringene øverst til høyre og nederst til venstre være partall, mens de to andre oppføringene er odde. Eller kanskje oppføringene øverst til høyre og nederst til venstre er delbare med 11, mens de to andre oppføringene begge er 1 mer enn et multiplum av 11.

Gruppene som kan defineres av denne typen relasjoner - og de modulære formene knyttet til slike grupper - er de mye studerte kongruensene.

Men de er som nåler i en høystakk: De fleste samlinger av 2 x 2 matriser kan ikke karakteriseres av fine regler på denne måten, noe som gjør dem og deres tilhørende modulære former til ikke-kongruens.

Det var ikke før på slutten av 1930-tallet - rundt starten av andre verdenskrig - at studiet av kongruensmodulære former begynte å formørke studiet av ikke-kongruens. Det var da den tyske matematikeren Erich Hecke utviklet en verktøykasse som ville tillate ham å finne mange egenskaper ved modulære former og assosiere dem med andre viktige matematiske objekter.

Heckes metoder fungerte bare for kongruensgrupper og deres modulære former. Ikke-kongruensgrupper manglet den ekstra strukturen som gjorde Heckes verktøykasse effektiv. "Denne tingen du har i kongruensverdenen går ut av døren når du flytter til ikkekongruensverdenen," sa Franc.

Og så det så ut til at ikke-kongruens modulære former var skjebnesvangre til alltid å bli oversett. Det er ikke å si at de ikke hadde noen form for egen struktur, som lurte rett under overflaten. Som Swinnerton-Dyers samarbeidspartner Bryan Birch en gang skrev: "Selv om strukturen er mer mystisk ser den ut til å være nesten like rik." Men når det kom til å få tilgang til den strukturen, var matematikere rådvill. De visste ikke engang hvor de skulle begynne.

Gå inn i Atkin og Swinnerton-Dyer.

Et ryddig kriterium

De to matematikerne ønsket å vite mer om ikke-kongruens modulære former, og hvilke hemmeligheter de måtte skjule.

"Det er alltid måten matematikken utvikler seg på," sa Winnie Li, en matematiker ved Pennsylvania State University. «Du studerer ting med helt spesielle egenskaper og mer struktur. Så går du for å generalisere det, for å prøve å forstå hvilke egenskaper som overføres og hvilke som ikke gjør det."

For å studere en gitt modulær form, representerer matematikere den ofte som en uendelig sum kalt en q-ekspansjon (en spesiell type potensserie), og analyser deretter koeffisientene til den utvidelsen. Det var allerede kjent at hvis en gitt modulær form er kongruens, så har koeffisientene nevnere som aldri blir større enn en fast verdi.

På 1960-tallet beregnet Atkin og Swinnerton-Dyer q-utvidelsene for poeng og poeng av modulære former. Mens de gjorde det, la de merke til at hvis en modulær form var ikke-kongruens, fortsatte nevnerne i den tilknyttede sekvensen å vokse uten binding. "De kunne faktisk si noe om disse mystiske ikke-kongruensformene," sa Yunqing Tang, en matematiker ved University of California, Berkeley.

Kan det faktisk være så enkelt å skille de to typene modulære former fra hverandre?

Matematikerne nevnte observasjonen deres på en konferanse i California i 1968, og antydet at ubegrensede nevnere kan være et universelt kjennetegn på ikke-kongruens-modulære former. Formodningen var "veldig slående," sa John Voight, en matematiker ved Dartmouth College. "Det gir oss et ryddig kriterium for å avgjøre om en modulær form tilhører en kongruensgruppe eller ikke" - en veldig praktisk lakmustest for tallteoretikere å ha til rådighet, og noe som i andre sammenhenger kan være vanskelig å oppdage.

"Det er nesten for godt til å være sant," la han til. "Man forventer egentlig ikke den slags mirakel."

Faktisk kunne ingen bevise den ubegrensede nevnerformodningen. Li og en håndfull andre var i stand til å vise det var sant for bestemte familier av ikke-kongruens modulære former, men matematikere hadde ingen anelse om hvordan de skulle takle det generelle utsagnet.

Så i september 2021, Tang, sammen med Frank Calegari fra University of Chicago og Fartøyet Dimitrov fra Institute for Advanced Study, la ut et 50-siders bevis. "Det var fantastisk og virkelig uventet," sa Franc. "Det føltes som om samfunnet ikke hadde noen ideer for hvordan de skulle nærme seg dette problemet."

Forfatterne håper papiret deres er det første skrittet mot å utvikle skiltet i ørkenen til et fullverdig veinett. "Vi gir vårt beskjedne bidrag til denne delen av tallteorien ved å gi svaret på det enkleste spørsmålet," sa Dimitrov.

Tilbake til gamle måter

Calegari, Dimitrov og Tang satte seg ikke for å løse den ubegrensede nevneren. På slutten av 2019 håpet de å vise at et visst tall (en verdi av en analog til Riemann zeta-funksjonen) var irrasjonelt - at det, som kvadratroten av 2, ikke kan skrives som en brøk. (Deres endelige mål er å bevise at dette tallet og andre lignende det er transcendentalt, noe som betyr at, som med tallene π og e, de kan ikke skrives som løsningen på en polynomligning med heltallskoeffisienter.)

Tilsynelatende er dette problemet helt urelatert. Men 1. januar 2021 ringte Dimitrov inn det nye året med en e-post til de andre der han beskrev «en ønsketenke»: Kanskje teknikkene de hadde utviklet i løpet av det foregående året kunne brukes på nytt for å bevise den ubegrensede nevnerens formodning.

De ga det en sjanse. Innen syv måneder hadde de sitt bevis.

Først vurderte de to rom: rommet til alle modulære former med avgrensede nevnere, og rommet til alle kongruensmodulære former. I følge formodningen om ubegrensede nevnere, skal disse to mellomrommene være identiske. Siden mellomrommene tilfredsstilte visse egenskaper, måtte matematikerne bare vise at de var like store. Å gjøre det vil automatisk innebære at de er likeverdige.

Calegari, Dimitrov og Tang kunne relativt enkelt beregne størrelsen på det andre rommet, og oppnå en slags grov telling av kongruensmodulære former. Men det var veldig vanskelig å få et størrelsesanslag på den første plassen. De måtte kombinere mange forskjellige teknikker - inkludert de fra transcendental tallteori.

Ved å bruke disse metodene viste de at rommet til modulære former med avgrensede nevnere kunne være høyst en viss størrelse. Den maksimale størrelsen var litt større enn størrelsen på rommet til kongruensmodulære former. Likevel viste dette trinnet seg å "virkelig være hjertet av beviset," sa Jean-Benoît Bost, matematiker ved Paris-Saclay University. "Du trenger mye mot for å gjøre det." (Calegari, Dimitrov og Tang beviste at dette var knyttet til størrelsen på plassen på en håndfull forskjellige måter, noe som potensielt ga teknikkene deres mye bredere anvendelser.)

"Det er veldig, veldig klassisk, vakker matematikk, med en smak av det 19. århundre," sa Javier Fresán, en matematiker ved École Polytechnique i Frankrike.

Trioen trengte da å tette gapet mellom de to rommene. Å gjøre det ville fastslå at enhver modulær form med avgrensede nevnere måtte være kongruens.

Så de antok det motsatte: at det eksisterer en ikke-kongruens modulær form med avgrensede nevnere. Per definisjon ville det leve i gapet som Calegari, Dimitrov og Tang prøvde å tette. De tre viste deretter at eksistensen av denne ikke-kongruens-modulære formen automatisk antydet eksistensen av mange andre ikke-kongruens-modulære former med avgrensede nevnere. Det var som om en hel skog hadde vokst fra det eneste frøet.

Men de hadde allerede etablert den maksimale størrelsen på gapet - og det var for lite til å passe så mange ikke-kongruensformer.

Noe som betydde at selv en slik form ikke kunne eksistere. De hadde bevist Atkin og Swinnerton-Dyers tiår gamle formodning.

Matematikere finner teknikkene som brukes i arbeidet enda mer spennende enn selve resultatet. "Disse ideene har aldri blitt brukt før i å studere aritmetikken til modulære former," sa Scholl.

Som Voight forklarer, selv om studiet av modulære former startet som en del av feltet kompleks analyse, har nåværende arbeid vært rekkevidden av tallteori og algebraisk geometri. Det nye papiret, sa han, markerer en retur til kompleks analyse: "Det er et forfriskende gammelt perspektiv."

Et søk etter nye teorier

Matematikere er ikke de eneste som er begeistret for antagelsen om ubegrensede nevnere. Det gjør også en opptreden i teoretisk fysikk.

På 1970-tallet utfoldet en annen historie seg parallelt med den som ble startet av Atkin og Swinnerton-Dyer. Matematikere hadde la merke til en merkelig sammenheng mellom et objekt kalt monstergruppen og en modulær form kalt j-funksjon. Koeffisientene til j-funksjon reflekterte nøyaktig visse egenskaper til monstergruppen.

Senere forskning avslørte at denne sammenhengen skyldtes det faktum at både gruppen og den modulære formen var relatert til en viktig modell av partikkelinteraksjoner kalt en todimensjonal konform feltteori.

Men den konforme feltteorien som knyttet monstergruppen til j-funksjon var bare ett eksempel på et uendelig antall konforme feltteorier. Og selv om disse teoriene ikke beskriver universet vi lever i, kan forståelsen av dem gi ny innsikt i hvordan mer realistiske kvantefeltteorier kan oppføre seg.

Og så fysikere har fortsatt å studere konforme feltteorier ved å se på deres tilhørende modulære former. (I denne sammenhengen bruker fysikere en mer generell forestilling om en modulær form, kalt en vektor-verdi modulær form.)

For å få tak i hva som skjer med en bestemt konform feltteori, må du vise at dens modulære form er kongruens, sa Michael Tuite, en matematiker og teoretisk fysiker ved University of Galway i Irland. Du kan deretter begynne å beskrive konforme feltteorier, og til og med oppdage nye du ikke visste å se etter. Dette er spesielt avgjørende for en pågående innsats for å klassifisere alle konforme feltteorier - et prosjekt som fysikere har kalt den modulære bootstrap.

"Når du vet at det er en kongruens modulær form, som lar deg gjøre enorme fremskritt i dette programmet," sa Mason.

Fysikere utviklet et rammeverk som lar dem anta denne kongruensegenskapen for de modulære formene de studerer. Men det er ikke det samme som å ha et strengt matematisk bevis - og mens andre matematikere senere var i stand til å gi et slikt bevis, deres argument fungerte bare i visse settinger. Det innebar også "en veldig kronglete, kronglete vei" mot kongruens, ifølge Mason, selv om han også påpekte at denne kronglete veien ga viktig innsikt.

Calegari, Dimitrov og Tangs bevis på de ubegrensede nevnerformodningene skjærer gjennom alt dette. Det er fordi, som det viser seg, de modulære formene knyttet til konforme feltteorier alltid har heltallskoeffisienter. Per definisjon har heltall en nevner på 1, noe som betyr at nevnerne deres alltid er avgrenset. Og siden antagelsen om ubegrensede nevnere sier at begrensede nevnere bare er assosiert med kongruensmodulære former, er det ikke lenger behov for å gjøre antakelser. "Du trenger ikke engang å vite noe om [konforme feltteorier]," sa Tang. Det nye beviset leverer automatisk kongruens for alle disse tilfellene – gratis.

"Det er noe som har vært i luften i flere tiår," sa Bost. Nå er det endelig løst.

"Det er virkelig et mirakel," sa Mason. "Dette følger bare mirakuløst av det faktum at disse sekvensene er heltall."

Han har allerede begynt å bruke resultatet i sitt eget arbeid. "Helt siden den dagen avisen dukket opp, har jeg brukt den," sa han. «Det gir en veldig velkommen snarvei til resultater som jeg ønsker å løse. …Det er å kutte ut en enorm mengde potensielt arbeid som jeg ikke kunne se veien gjennom.»

Det setter også det modulære bootstrap-programmet og andre resultater på et sterkere matematisk grunnlag. "Dette kommer til å tillate matematikere å bevise [tidligere] resultater, eller tro dem," sa Mason.

"Jeg tror det virkelig kommer til å ha en innvirkning, spesielt på matematikksiden, bare for å virkelig, virkelig binde ting sammen, for å forstå nøyaktig hva som skjer," sa Tuite.

Matematisk transcendens

I året siden de la ut beviset, har Calegari, Dimitrov og Tang fortsatt samarbeidet. De har nå vendt tilbake til den typen problemer i transcendental tallteori som opprinnelig vekket interessen deres for formodningen. "Vi prøver å fullføre det vi startet," sa Tang. Faktisk har de allerede brukt teknikkene sine for å bevise at flere tall av interesse er irrasjonelle.

"De presser virkelig [metoden] til det ytterste," sa Fresán. "Jeg er veldig spent på dette."

Disse metodene kan også være anvendelige på andre problemer innen tallteori.

Bortsett fra teknikker, markerer oppløsningen av antagelsen om ubegrensede nevnere en av de første store milepælene i arbeidet med å få en bedre forståelse av modulære former for ikke-kongruens. "Dette er en fantastisk prestasjon, at vi kan gjøre noen fremskritt med ikke-kongruensformer på denne måten," sa Franc. "Jeg er spent på de neste 10, 20 årene for å se hva som skjer."

Li, Voight og andre begynner allerede å lete etter mønstre i den typen tall som dukker opp i nevnerne til disse mystiske modulformene. De håper at de ved å gjøre det kan finne hint til dypere struktur.

"Denne antagelsen om ubegrensede nevnere var bare begynnelsen," sa Li.