1ICFO-Institut de Ciencies Fotoniques, Барселонский институт науки и технологий, 08860 Кастельдефельс, Испания
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 Барселона, Испания
3Univ Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Гренобль, Франция
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Барселона, Испания
Находите эту статью интересной или хотите обсудить? Scite или оставить комментарий на SciRate.
Абстрактные
Взаимно несмещенные базы соответствуют очень полезным парам измерений в квантовой теории информации. Известно, что в наименьшем составном измерении, шести, существует от трех до семи взаимно несмещенных базисов, при этом гипотеза десятилетней давности, известная как гипотеза Цаунера, утверждает, что существует не более трех. Здесь мы решаем гипотезу Цаунера численно, строя неравенства Белла для каждой пары целых чисел $n,d ge 2$, которые могут быть максимально нарушены в размерности $d$ тогда и только тогда, когда в этой размерности существует $n$ MUB. Следовательно, мы превращаем гипотезу Цаунера в проблему оптимизации, которую мы решаем с помощью трех численных методов: оптимизация на качелях, нелинейное полуопределенное программирование и методы Монте-Карло. Все три метода правильно идентифицируют известные случаи в малых размерностях, и все предполагают, что не существует четырех взаимно несмещенных оснований в шестом измерении, причем все они находят одни и те же основания, которые численно оптимизируют соответствующее неравенство Белла. Более того, эти численные оптимизаторы, по-видимому, совпадают с «четырьмя самыми удаленными основаниями» в шестом измерении, найденными путем численной оптимизации меры расстояния в [P. Рейналь, X. Лю, Б.-Г. Энглерт, {Phys. Rev. A}, {83} 062303 (2011)]. Наконец, результаты Монте-Карло предполагают, что в десятом измерении существует не более трех MUB.
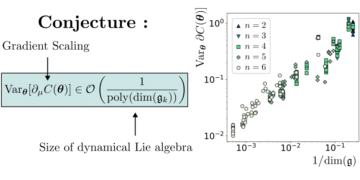
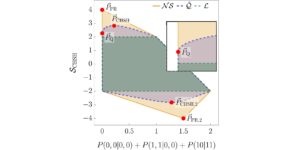
Рекомендуемое изображение: относительная разница между значением наших неравенств Белла при условии, что n MUB существуют в измерении d, и значением, найденным нашими численными методами. Нулевые значения означают, что методы нашли n MUB в измерении d, а ненулевые значения означают, что методы не нашли n MUB в измерении d. Все известные случаи (размеры со второго по пятый и размерность шесть с двумя и тремя MUB) правильно идентифицируются цифрами. В шестом измерении ни один из методов не находит четырех MUB, и все методы сходятся к одному и тому же набору из четырех оснований.
Популярное резюме
Несмотря на их широкое использование, все еще остаются открытыми вопросы относительно структуры MUB. Наиболее заметно, что максимальное количество попарно несмещенных измерений («количество MUB») неизвестно, если размерность квантовой системы является составным числом. В частности, в шестом измерении мы знаем только, что количество MUB составляет от трех до семи. Давняя открытая гипотеза - это гипотеза Заунера, утверждающая, что в шестом измерении существует не более трех MUB. Эта многолетняя гипотеза подтверждается некоторыми числовыми данными, но до сих пор не существует никаких доказательств.
В этой работе мы рассматриваем гипотезу Заунера через нелокальность Белла. Нелокальность Белла касается двух экспериментаторов, которым не разрешено общаться, но которые могут иметь общие корреляции в форме классической случайности или общего квантового состояния. Было показано, что совместное использование квантовых ресурсов может привести к экспериментальным данным, которые не могут быть объяснены классической физикой (точнее, так называемыми моделями локальных скрытых переменных). Это известно как теорема Белла, и в последнее десятилетие она была подтверждена экспериментально. Подтверждение неклассичности экспериментальных данных чаще всего осуществляется с помощью так называемых неравенств Белла, которые являются функциями вероятностей результатов измерения, возникающих в эксперименте. Классические данные должны удовлетворять неравенствам Белла, тогда как квантовые данные могут их нарушать.
Недавно были обнаружены неравенства Белла, которые максимально нарушаются, если одна из сторон использует пару измерений MUB заданной размерности. В данной работе мы расширяем эти неравенства до новых, максимально нарушаемых выбранным числом измерений МУБ в заданной размерности. Более того, если размерность в эксперименте фиксирована, то максимальное нарушение достигается тогда и только тогда, когда используемые измерения соответствуют выбранному числу МВБ в данной размерности. Следовательно, определение того, существует ли выбранное количество MUB в данном измерении, эквивалентно нахождению максимального нарушения соответствующего неравенства Белла в этом фиксированном измерении.
Хотя нахождение этого максимального нарушения в целом является сложной задачей, мы используем три различных численных метода в попытке найти максимальное нарушение наших неравенств Белла в фиксированной размерности. Два из этих методов являются вариантами методов полуопределенного программирования, а третий вдохновлен статистической физикой и называется моделируемым отжигом. Хотя все эти методы эвристичны, то есть нет гарантии, что они найдут истинный оптимум задачи, можно оценить их эффективность, применяя их к задачам оптимизации, оптимум которых известен. В частности, мы обнаружили, что все три метода способны правильно идентифицировать измерения MUB в тех случаях, когда известно, что они существуют. Кроме того, в тех случаях, когда известно, что их не существует, все три метода сходятся к одному и тому же набору измерений с точностью до численной точности. Затем мы применяем наши методы к первому неизвестному случаю, то есть к четырем MUB в шестом измерении. Ни один из методов не может идентифицировать четыре MUB в шестом измерении, но опять же все они сходятся к одному и тому же набору четырех измерений с точностью до числовой точности. Кроме того, метод имитации отжига не находит четырех MUB в следующем составном измерении, десятом измерении. Следовательно, хотя строгие утверждения не могут быть сделаны из-за эвристического характера наших методов, наши результаты подтверждают гипотезу Цаунера с новой точки зрения нелокальности Белла.
► Данные BibTeX
► Рекомендации
[1] ИД Иванович. Геометрическое описание определения квантового состояния. Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019.
https://doi.org/10.1088/0305-4470/14/12/019
[2] Г. Брассард CH Беннетт. Квантовая криптография: распространение открытых ключей и подбрасывание монет. Материалы Международной конференции IEEE по компьютерам, системам и обработке сигналов (IEEE, 1984), 175:8, 1984. doi:10.1016/j.tcs.2011.08.039.
https: / / doi.org/ 10.1016 / j.tcs.2011.08.039
[3] Артур К. Экерт. Квантовая криптография на основе теоремы Белла. физ. Rev. Lett., 67:661–663, 1991. doi:10.1103/PhysRevLett.67.661.
https: / / doi.org/ 10.1103 / PhysRevLett.67.661
[4] Дагмар Брюс. Оптимальное прослушивание в квантовой криптографии с шестью состояниями. физ. Rev. Lett., 81:3018–3021, 1998. doi:10.1103/PhysRevLett.81.3018.
https: / / doi.org/ 10.1103 / PhysRevLett.81.3018
[5] Армин Таваколи, Аллей Хамиди, Брено Маркес и Мохамед Буреннан. Квантовые коды случайного доступа, использующие одиночные системы $d$-уровня. физ. Rev. Lett., 114:170502, 2015. doi:10.1103/PhysRevLett.114.170502.
https: / / doi.org/ 10.1103 / PhysRevLett.114.170502
[6] Мате Фаркаш и Енджей Каневски. Самопроверка взаимно непредвзятых оснований в сценарии «подготовка и измерение». физ. Rev. A, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316.
https: / / doi.org/ 10.1103 / PhysRevA.99.032316
[7] Х. Бехманн-Паскинуччи и Н. Гизин. Неравенство Белла для кванитов с бинарными измерениями. Квантовая информация. Comput., 3(2):157–164, 2003. doi:10.26421/QIC3.2-6.
https: / / doi.org/ 10.26421 / QIC3.2-6
[8] Енджей Каневски, Иван Шупич, Хорди Тура, Флавио Баккари, Алексия Салавракос и Ремигиуш Аугусяк. Максимальная нелокальность из максимальной запутанности и взаимно несмещенных базисов и самотестирование двухкутритных квантовых систем. Quantum, 3:198, 2019. doi:10.22331/q-2019-10-24-198.
https://doi.org/10.22331/q-2019-10-24-198
[9] Армин Таваколи, Мате Фаркаш, Денис Россе, Жан-Даниэль Банкаль и Енджей Каневски. Взаимно несмещенные базы и симметричные информационно полные измерения в экспериментах Белла. Science Advances, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847.
https:///doi.org/10.1126/sciadv.abc3847
[10] Томас Дюрт, Бертольд-Георг Энглерт, Ингемар Бенгтссон и Кароль Жычковски. На взаимно непредвзятых основаниях. Международный журнал квантовой информации, 08(04):535–640, 2010. doi:10.1142/S0219749910006502.
https: / / doi.org/ 10.1142 / S0219749910006502
[11] Уильям К. Вуттерс и Брайан Д. Филдс. Оптимальное определение состояния по взаимно несмещенным измерениям. Annals of Physics, 191(2):363–381, 1989. doi:10.1016/0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
[12] Павел Воцян и Томас Бет. Новая конструкция взаимно несмещенных базисов в квадратных измерениях. Квантовая информация. Comput., 5(2):93–101, 2005. doi:10.26421/QIC5.2-1.
https: / / doi.org/ 10.26421 / QIC5.2-1
[13] Михай Вайнер. Зазор для максимального количества взаимно несмещенных оснований. проц. амер. Мат. Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] Герхард Заунер. Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. Кандидатская диссертация, 1999.
[15] П. Оскар Бойкин, Мира Ситарам, Фам Хуу Тиеп и Павел Вочан. Взаимно несмещенные базисы и ортогональные разложения алгебр Ли. Квантовая информация. Comput., 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https: / / doi.org/ 10.26421 / QIC7.4-6
[16] Стивен Брайерли и Стефан Вейгерт. Построение взаимно несмещенных базисов в размерности шесть. физ. Rev. A, 79:052316, 2009. doi:10.1103/PhysRevA.79.052316.
https: / / doi.org/ 10.1103 / PhysRevA.79.052316
[17] Филипп Джаминг, Мате Матолчи, Петер Мора, Ференц Соллёши и Михай Вайнер. Обобщенная проблема Паули и бесконечное семейство MUB-троек в размерности 6. Journal of Physics A: Mathematical and Theoretical, 42(24):245305, май 2009 г. doi:10.1088/1751-8113/42/24/ 245305.
https://doi.org/10.1088/1751-8113/42/24/245305
[18] Гэри МакКоннелл, Гарри Спенсер и Афак Тахир. Доказательства за и против гипотезы MUB Заунера в $mathbb{C}^6$. 2021. doi:10.48550/arXiv.2103.08703.
https:///doi.org/10.48550/arXiv.2103.08703
[19] Сандер Гриблинг и Свен Полак. Взаимно несмещенные базисы: полиномиальная оптимизация и симметрия. 2021. doi:10.48550/arXiv.2111.05698.
https:///doi.org/10.48550/arXiv.2111.05698
[20] Ингемар Бенгтссон, Войцех Брузда, Оса Эрикссон, Ян-Оке Ларссон, Войцех Тадей и Кароль Жычковски. Взаимно несмещенные базисы и матрицы Адамара шестого порядка. Журнал математической физики, 48(5):052106, 2007. doi:10.1063/1.2716990.
https: / / doi.org/ 10.1063 / 1.2716990
[21] Филипп Рейналь, Синь Лю и Бертольд-Георг Энглерт. Взаимно несмещенные основания в шести измерениях: четыре самых удаленных основания. физ. Rev. A, 83:062303, 2011. doi:10.1103/PhysRevA.83.062303.
https: / / doi.org/ 10.1103 / PhysRevA.83.062303
[22] Эдгар А. Агилар, Якуб Й. Боркала, Петр Миронович и Марцин Павловский. Связи между взаимно несмещенными базисами и квантовыми кодами случайного доступа. физ. Rev. Lett., 121:050501, 2018. doi:10.1103/PhysRevLett.121.050501.
https: / / doi.org/ 10.1103 / PhysRevLett.121.050501
[23] Николя Бруннер, Даниэль Кавальканти, Стефано Пиронио, Валерио Скарани и Стефани Венер. Белл нелокальность. Ред. Мод. Phys., 86: 419–478, 2014. DOI: 10.1103 / RevModPhys.86.419.
https: / / doi.org/ 10.1103 / RevModPhys.86.419
[24] МОСЕК АПС. MOSEK Fusion API для C++ 9.2.49, 2021 г. URL: https:///docs.mosek.com/9.2/cxxfusion/index.html.
https:///docs.mosek.com/9.2/cxxfusion/index.html
[25] Хироши Ямасита, Хироши Ябэ и Кохей Харада. Метод прямой двойственной внутренней точки для нелинейного полуопределенного программирования. Математическое программирование, 135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z.
HTTPS: / / doi.org/ 10.1007 / s10107-011-0449-г
[26] Стивен Бойд и Ливен Ванденберге. Выпуклая оптимизация. Издательство Кембриджского университета, 2004. DOI: 10.1017 / CBO9780511804441.
https: / / doi.org/ 10.1017 / CBO9780511804441
[27] С. Киркпатрик, К. Д. Гелатт и М. П. Векки. Оптимизация путем имитации отжига. Science, 220(4598):671–680, 1983. doi:10.1126/science.220.4598.671.
https: / / doi.org/ 10.1126 / science.220.4598.671
[28] Николас Метрополис, Арианна В. Розенблут, Маршалл Н. Розенблут, Августа Х. Теллер и Эдвард Теллер. Уравнение расчета состояний на быстрых вычислительных машинах. Журнал химической физики, 21(6):1087–1092, 1953. doi:10.1063/1.1699114.
https: / / doi.org/ 10.1063 / 1.1699114
[29] Мигель Наваскуэс, Стефано Пиронио и Антонио Асин. Ограничение множества квантовых корреляций. физ. Rev. Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401.
https: / / doi.org/ 10.1103 / PhysRevLett.98.010401
Цитируется
Эта статья опубликована в Quantum под Creative Commons Attribution 4.0 International (CC BY 4.0) лицензия. Авторское право остается за первоначальными правообладателями, такими как авторы или их учреждения.