Nytt genombrott för matrismultiplikation närmare ideal | Quanta Magazine

Datavetare är ett krävande gäng. För dem räcker det inte att få rätt svar på ett problem – målet är nästan alltid att få svaret så effektivt som möjligt.

Utför handlingen att multiplicera matriser, eller matriser av tal. 1812 kom den franske matematikern Jacques Philippe Marie Binet med den grundläggande uppsättning regler vi fortfarande lär eleverna. Det fungerar alldeles utmärkt, men andra matematiker har hittat sätt att förenkla och påskynda processen. Nu uppgiften att påskynda processen av matrismultiplikation ligger i skärningspunkten mellan matematik och datavetenskap, där forskare fortsätter att förbättra processen till denna dag - även om vinsterna under de senaste decennierna har varit ganska blygsamma. Sedan 1987 har numeriska förbättringar i matrismultiplikation varit "små och ... extremt svåra att få", sa François Le Gall, en datavetare vid Nagoya University.

Nu har tre forskare - Ran Duan och Renfei Zhou från Tsinghua University och Hongxun Wu från University of California, Berkeley - tagit ett stort steg framåt för att attackera detta fleråriga problem. Deras nya resultat, som presenterades i november förra året på Foundations of Computer Science-konferensen, härrör från en oväntad ny teknik, sade Le Gall. Även om förbättringen i sig var relativt liten, kallade Le Gall den "konceptuellt större än andra tidigare."

Tekniken avslöjar en tidigare okänd och därmed outnyttjad källa till potentiella förbättringar, och den har redan burit frukt: Ett andra papper, publicerad i januari, bygger på den första som visar hur matrismultiplikation kan ökas ytterligare.

"Detta är ett stort tekniskt genombrott," sa William Kuszmaul, en teoretisk datavetare vid Harvard University. "Det är den största förbättringen av matrismultiplikation vi har sett på mer än ett decennium."

Enter the Matrix

Det kan verka som ett dunkelt problem, men matrismultiplikation är en grundläggande beräkningsoperation. Det är inkorporerat i en stor del av de algoritmer som människor använder varje dag för en mängd olika uppgifter, från att visa skarpare datorgrafik till att lösa logistiska problem i nätverksteori. Och precis som inom andra beräkningsområden är hastigheten avgörande. Även små förbättringar kan så småningom leda till betydande besparingar av tid, beräkningskraft och pengar. Men för närvarande är teoretiker främst intresserade av att ta reda på hur snabb processen någonsin kan vara.

Det traditionella sättet att multiplicera två n-förbi-n matriser — genom att multiplicera siffror från varje rad i den första matrisen med siffror i kolumnerna i den andra — kräver n³ separata multiplikationer. För 2-av-2-matriser betyder det 2³ eller 8 multiplikationer.

1969 avslöjade matematikern Volker Strassen en mer komplicerad procedur som kunde multiplicera 2 gånger 2 matriser i bara sju multiplikationssteg och 18 additioner. Två år senare visade datavetaren Shmuel Winograd att sju verkligen är det absoluta minimumet för 2 x 2 matriser.

Strassen utnyttjade samma idé för att visa att allt större n-förbi-n matriser kan också multipliceras med färre än n³ steg. Ett nyckelelement i denna strategi involverar en procedur som kallas nedbrytning - att bryta ner en stor matris i successivt mindre submatriser, som kan sluta vara så små som 2-av-2 eller till och med 1-by-1 (detta är bara enstaka siffror).

Skälet för att dela upp en gigantisk array i små bitar är ganska enkel, enligt Virginia Vassilevska Williams, en datavetare vid Massachusetts Institute of Technology och medförfattare till en av de nya tidningarna. "Det är svårt för en människa att titta på en stor matris (säg i storleksordningen 100 gånger 100) och tänka på den bästa möjliga algoritmen," sa Vassilevska Williams. Även 3-av-3-matriser har inte lösts helt än. "Ändå kan man använda en snabb algoritm som man redan har utvecklat för små matriser för att även få en snabb algoritm för större matriser."

Nyckeln till hastighet, har forskare bestämt, är att minska antalet multiplikationssteg, vilket sänker exponenten från n³ (för standardmetoden) så mycket de kan. lägsta möjliga värde, n², är i princip så lång tid det tar att bara skriva svaret. Datavetare hänvisar till den exponenten som omega, ω, med n^ω är det minsta möjliga steget som behövs för att framgångsrikt multiplicera två n-förbi-n matriser som n växer sig mycket stor. "Poängen med detta arbete," sade Zhou, som också var medförfattare till uppsatsen från januari 2024, "är att se hur nära två du kan komma och om det kan uppnås i teorin."

Ett laserfokus

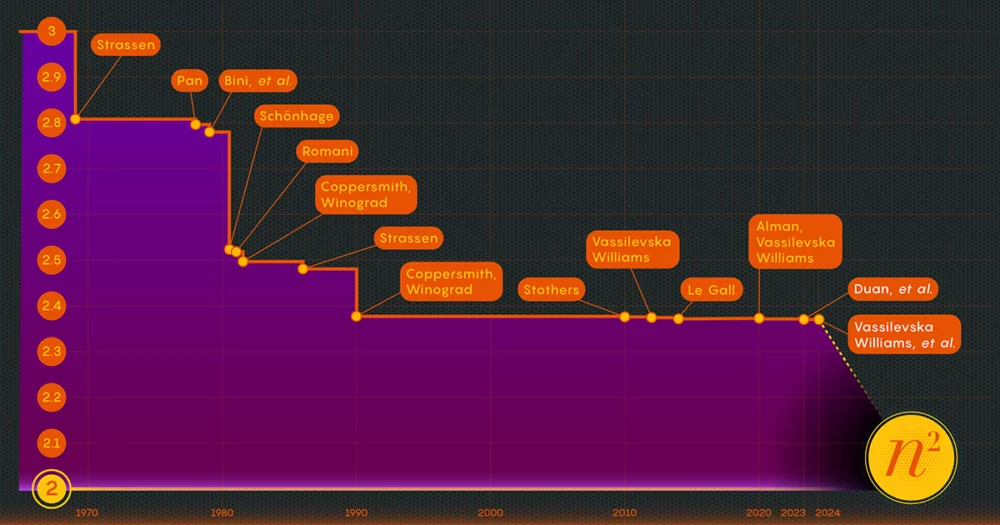
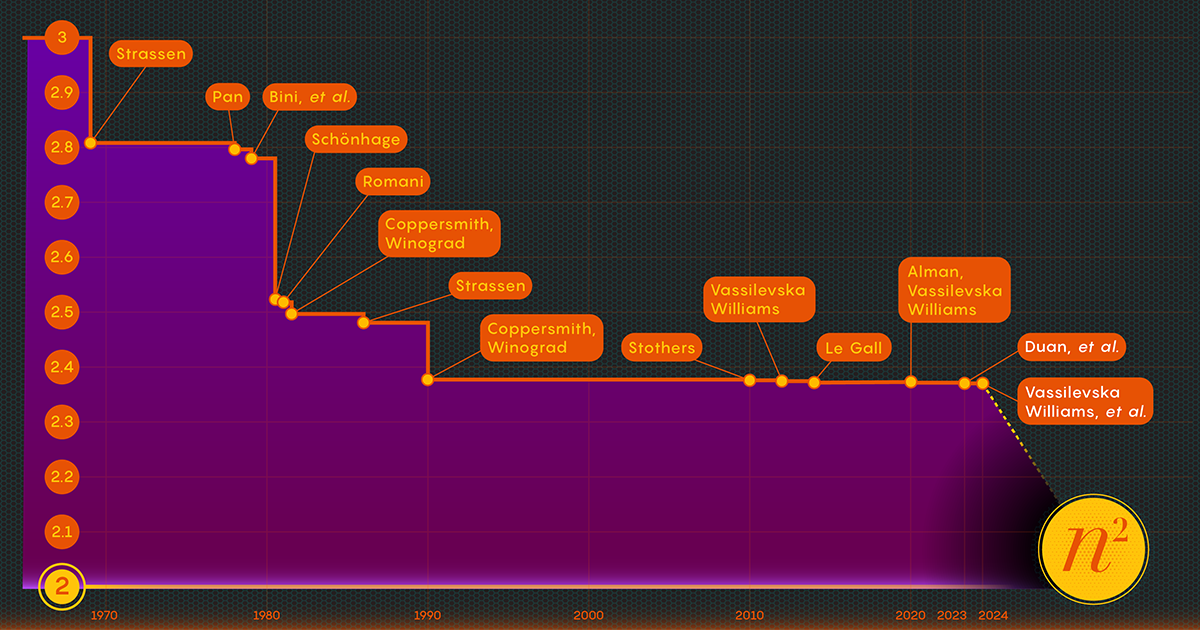
1986 fick Strassen ännu ett stort genombrott när han introducerade det som kallas lasermetoden för matrismultiplikation. Strassen använde det för att fastställa ett övre värde för omega på 2.48. Även om metoden bara är ett steg i stora matrismultiplikationer, är den en av de viktigaste eftersom forskare har fortsatt att förbättra den.

Ett år senare introducerade Winograd och Don Coppersmith en ny algoritm som på ett vackert sätt kompletterade lasermetoden. Denna kombination av verktyg har varit med i praktiskt taget alla efterföljande försök att påskynda matrismultiplikationen.

Här är ett förenklat sätt att tänka på hur dessa olika element passar ihop. Låt oss börja med två stora matriser, A och B, som du vill multiplicera tillsammans. Först bryter du ner dem i många mindre submatriser, eller block, som de ibland kallas. Därefter kan du använda Coppersmith och Winograds algoritm för att fungera som en slags bruksanvisning för hantering och slutligen montering av blocken. "Den talar om för mig vad jag ska multiplicera och vad jag ska lägga till och vilka poster som går vart" i produktmatrisen C, sa Vassilevska Williams. "Det är bara ett recept för att bygga upp C från A och B."

Det finns dock en hake: Du hamnar ibland med block som har poster gemensamma. Att lämna dessa i produkten skulle vara ungefär som att räkna dessa poster två gånger, så någon gång måste du bli av med de duplicerade termerna, så kallade överlappningar. Forskare gör detta genom att "döda" blocken de befinner sig i - sätta deras komponenter lika med noll för att ta bort dem från beräkningen.

Det är där Strassens lasermetod äntligen kommer in i bilden. "Lasermetoden fungerar vanligtvis mycket bra och hittar i allmänhet ett bra sätt att döda en delmängd av block för att ta bort överlappningen," sa Le Gall. Efter att lasern har eliminerat, eller "bränt bort", alla överlappningar kan du konstruera den slutliga produktmatrisen, C.

Att sätta ihop dessa olika tekniker resulterar i en algoritm för att multiplicera två matriser med ett medvetet snålt antal multiplikationer totalt sett - åtminstone i teorin. Lasermetoden är inte avsedd att vara praktisk; det är bara ett sätt att tänka på det ideala sättet att multiplicera matriser. "Vi kör aldrig metoden [på en dator]," sa Zhou. "Vi analyserar det."

Och den analysen är det som ledde till den största förbättringen av omega på mer än ett decennium.

En förlust har hittats

Förra sommarens tidning, av Duan, Zhou och Wu, visade att Strassens process fortfarande kunde påskyndas avsevärt. Det var allt på grund av ett koncept som de kallade en dold förlust, begravd djupt i tidigare analyser - "ett resultat av att oavsiktligt dödade för många block", sa Zhou.

Lasermetoden fungerar genom att märka block med överlappningar som sopor, planerade för bortskaffande; andra block anses värda och kommer att sparas. Urvalsprocessen är dock något randomiserad. Ett block som klassats som skräp kan i själva verket visa sig vara användbart trots allt. Detta var inte en total överraskning, men genom att undersöka många av dessa slumpmässiga val, fastställde Duans team att lasermetoden systematiskt undervärderade block: Fler block borde sparas och färre kastas ut. Och, som vanligtvis är fallet, leder mindre avfall till högre effektivitet.

"Att kunna behålla fler block utan överlappning leder alltså till ... en snabbare matrismultiplikationsalgoritm," sa Le Gall.

Efter att ha bevisat förekomsten av denna förlust modifierade Duans team sättet att lasermetoden märkte block, vilket minskade avfallet avsevärt. Som ett resultat satte de en ny övre gräns för omega vid cirka 2.371866 - en förbättring jämfört med den tidigare övre gränsen på 2.3728596, inställd 2020 av Josh Alman och Vassilevska Williams. Det kan tyckas vara en blygsam förändring, som sänker gränsen med ungefär 0.001. Men det är den enskilt största förbättringen som forskare har sett sedan 2010. Vassilevska Williams och Almans resultat för 2020, som jämförelse, förbättrades endast med 0.00001 jämfört med sin föregångare.

Men det som är mest spännande för forskare är inte bara själva den nya skivan – som inte varade länge. Det är också det faktum att tidningen avslöjade en ny väg för förbättringar som fram till dess hade gått helt obemärkt förbi. I nästan fyra decennier har alla förlitat sig på samma lasermetod, sa Le Gall. "Då upptäckte de att vi kan göra bättre."

Uppsatsen från januari 2024 förfinade detta nya tillvägagångssätt, vilket gjorde det möjligt för Vassilevska Williams, Zhou och deras medförfattare att ytterligare minska den dolda förlusten. Detta ledde till en ytterligare förbättring av omegas övre gräns, vilket minskade den till 2.371552. Författarna generaliserade också samma teknik för att förbättra multiplikationsprocessen för rektangulära (n-förbi-m) matriser — en procedur som har tillämpningar inom grafteori, maskininlärning och andra områden.

Några ytterligare framsteg längs dessa linjer är nästan säkra, men det finns gränser. 2015, Le Gall och två medarbetare visat att den nuvarande metoden - lasermetoden i kombination med Coppersmith-Winograd-receptet - inte kan ge en omega under 2.3078. För att göra några ytterligare förbättringar, sa Le Gall, "måste du förbättra den ursprungliga [metoden] av Coppersmith och Winograd som egentligen inte har förändrats sedan 1987. " Men än så länge har ingen kommit på ett bättre sätt. Det kanske inte ens finns en.

"Att förbättra omega är faktiskt en del av att förstå detta problem," sa Zhou. "Om vi ​​kan förstå problemet väl kan vi designa bättre algoritmer för det. [Och] människor är fortfarande i de mycket tidiga stadierna av att förstå detta urgamla problem."