Elliptisk kurva "Murmurations" hittas med AI Take Flight | Quanta Magazine

Elliptiska kurvor är bland de mer lockande föremålen i modern matematik. De verkar inte komplicerade, men de bildar en motorväg mellan matematiken som många människor lär sig på gymnasiet och forskning om matematik när den är som mest abstru. De var centrala i Andrew Wiles berömda bevis på Fermats sista sats på 1990-talet. De är nyckelverktyg i modern kryptografi. Och år 2000 namngav Clay Mathematics Institute a gissningar om statistiken av elliptiska kurvor ett av sju "Millennium Prize Problems", som vart och ett har ett pris på 1 miljon dollar för sin lösning. Den gissningen, som först vågades av Bryan Birch och Peter Swinnerton-Dyer på 1960-talet, har fortfarande inte bevisats.

Att förstå elliptiska kurvor är en höginsats som har varit central för matematik. Så 2022, när ett transatlantiskt samarbete använde statistiska tekniker och artificiell intelligens för att upptäcka helt oväntade mönster i elliptiska kurvor, var det ett välkommet, om än oväntat, bidrag. "Det var bara en tidsfråga innan maskininlärning landade på vår ytterdörr med något intressant," sa Peter Sarnak, en matematiker vid Institutet för avancerade studier och Princeton University. Till en början kunde ingen förklara varför de nyupptäckta mönstren existerar. Sedan dess, i en serie nya artiklar, har matematiker börjat låsa upp orsakerna bakom mönstren, kallat "murringar" för deras likhet med de flytande formerna hos flockande starar, och har börjat bevisa att de inte bara måste förekomma i det speciella exempel undersöktes 2022, men i elliptiska kurvor mer generellt.

Vikten av att vara elliptisk

För att förstå vad dessa mönster är måste vi lägga en liten grund kring vad elliptiska kurvor är och hur matematiker kategoriserar dem.

En elliptisk kurva relaterar kvadraten på en variabel, vanligen skriven som y, till tredje makten av en annan, vanligen skriven som x: y² = x³ + Ax + B, för något par av nummer A och B, Så länge som A och B uppfylla några enkla villkor. Denna ekvation definierar en kurva som kan ritas i ett diagram på planet, som visas nedan. (Trots likheten i namnen är en ellips inte en elliptisk kurva.)

Även om de ser enkla ut, visar sig elliptiska kurvor vara otroligt kraftfulla verktyg för talteoretiker - matematiker som letar efter mönster i heltal. Istället för att låta variablerna x och y intervall över alla tal, matematiker gillar att begränsa dem till olika talsystem, som de kallar att definiera en kurva "över" ett givet talsystem. Elliptiska kurvor begränsade till de rationella talen - tal som kan skrivas som bråk - är särskilt användbara. "Elliptiska kurvor över de reella eller komplexa talen är ganska tråkiga," sa Sarnak. "Det är bara de rationella siffrorna som är djupa."

Här är ett sätt som är sant. Om du drar en rät linje mellan två rationella punkter på en elliptisk kurva, kommer platsen där den linjen skär kurvan igen också att vara rationell. Du kan använda detta faktum för att definiera "addition" i en elliptisk kurva, som visas nedan.

Dra en linje mellan P och Q. Den linjen kommer att skära kurvan vid en tredje punkt, R. (Matematiker har ett speciellt knep för att hantera fallet där linjen inte skär kurvan genom att lägga till en "punkt i oändligheten.") Reflexionen av R över x-axel är din summa P + Q. Tillsammans med denna additionsoperation bildar alla lösningar till kurvan ett matematiskt objekt som kallas en grupp.

Matematiker använder detta för att definiera "rangen" för en kurva. De rankningen av en kurva relaterar till antalet rationella lösningar den har. Rank 0-kurvor har ett ändligt antal lösningar. Kurvor med högre rang har ett oändligt antal lösningar vars förhållande till varandra med hjälp av additionsoperationen beskrivs av rangordningen.

Rangen förstås inte väl; matematiker har inte alltid ett sätt att beräkna dem och vet inte hur stora de kan bli. (Den största exakta rangordningen som är känd för en specifik kurva är 20.) Kurvor som ser liknande ut kan ha helt olika rangordningar.

Elliptiska kurvor har också mycket att göra med primtal, som bara är delbara med 1 och sig själva. I synnerhet tittar matematiker på kurvor över ändliga fält - system av cyklisk aritmetik som definieras för varje primtal. Ett ändligt fält är som en klocka med antalet timmar lika med primtal: Om du fortsätter att räkna uppåt börjar siffrorna om igen. I det finita fältet för 7, till exempel, är 5 plus 2 lika med noll och 5 plus 3 är lika med 1.

En elliptisk kurva har en tillhörande talföljd, kallad a_p, som relaterar till antalet lösningar som finns till kurvan i det finita fältet som definieras av primtal p. En mindre a_p betyder fler lösningar; en större a_p innebär färre lösningar. Även om rangen är svår att beräkna, sekvensen a_p är mycket lättare.

På grundval av många beräkningar gjorda på en av de allra första datorerna, antog Birch och Swinnerton-Dyer ett samband mellan en elliptisk kurvas rang och sekvensen a_p. Alla som kan bevisa att de hade rätt kommer att vinna en miljon dollar och matematisk odödlighet.

Ett överraskningsmönster dyker upp

Efter pandemins början, Yang-Hui He, en forskare vid London Institute for Mathematical Sciences, bestämde sig för att ta sig an några nya utmaningar. Han hade studerat fysik på college och hade tagit sin doktorsexamen från Massachusetts Institute of Technology i matematisk fysik. Men han blev allt mer intresserad av sifferteori, och med tanke på den ökande förmågan hos artificiell intelligens tänkte han att han skulle försöka sig på att använda AI som ett verktyg för att hitta oväntade mönster i siffror. (Det hade han redan varit med hjälp av maskininlärning att klassificera Calabi-Yau grenrör, matematiska strukturer som används i stor utsträckning inom strängteorin.)

I augusti 2020, när pandemin fördjupades, tog University of Nottingham emot honom för en online -prat. Han var pessimistisk om sina framsteg och om själva möjligheten att använda maskininlärning för att avslöja ny matematik. "Hans berättelse var att talteorin var svår eftersom man inte kunde maskinlära saker i talteorin," sa Thomas Oliver, en matematiker vid University of Westminster som var i publiken. Som han minns: ”Jag kunde inte hitta något eftersom jag inte var en expert. Jag använde inte ens rätt saker för att titta på det här.”

Oliver och Kyu-Hwan Lee, en matematiker vid University of Connecticut, började arbeta med He. "Vi bestämde oss för att göra det här bara för att lära oss vad maskininlärning var, snarare än att på allvar studera matematik," sa Oliver. "Men vi upptäckte snabbt att man kunde maskinlära sig många saker."

Oliver och Lee föreslog att han skulle tillämpa sina tekniker för att undersöka L-funktioner, oändliga serier nära besläktade med elliptiska kurvor genom sekvensen a_p. De kan använda en onlinedatabas med elliptiska kurvor och deras relaterade L-funktioner som kallas LMFDB att träna sina maskininlärningsklassificerare. Då hade databasen lite över 3 miljoner elliptiska kurvor över rationalerna. I oktober 2020 hade de ett papper som använde information hämtad från L-funktioner för att förutsäga en viss egenskap hos elliptiska kurvor. I november delade de ett annat papper som använde maskininlärning för att klassificera andra objekt i talteorin. I december kunde de förutsäga rangen av elliptiska kurvor med hög noggrannhet.

Men de var inte säkra på varför deras maskininlärningsalgoritmer fungerade så bra. Lee frågade sin student Alexey Pozdnyakov för att se om han kunde ta reda på vad som pågick. När det händer sorterar LMFDB elliptiska kurvor enligt en kvantitet som kallas ledaren, som sammanfattar information om primtal för vilka en kurva inte fungerar bra. Så Pozdnyakov försökte titta på ett stort antal kurvor med liknande ledare samtidigt - säg alla kurvor med ledare mellan 7,500 10,000 och XNUMX XNUMX.

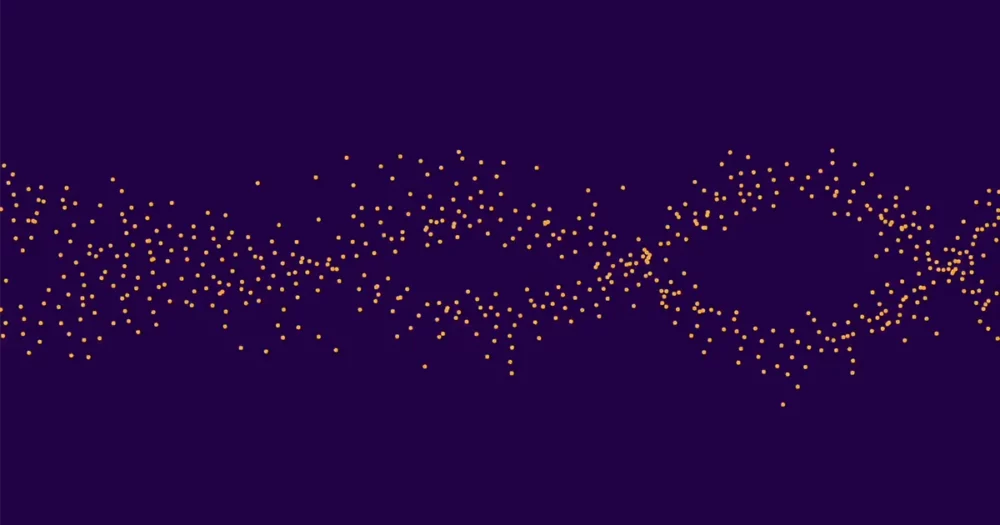
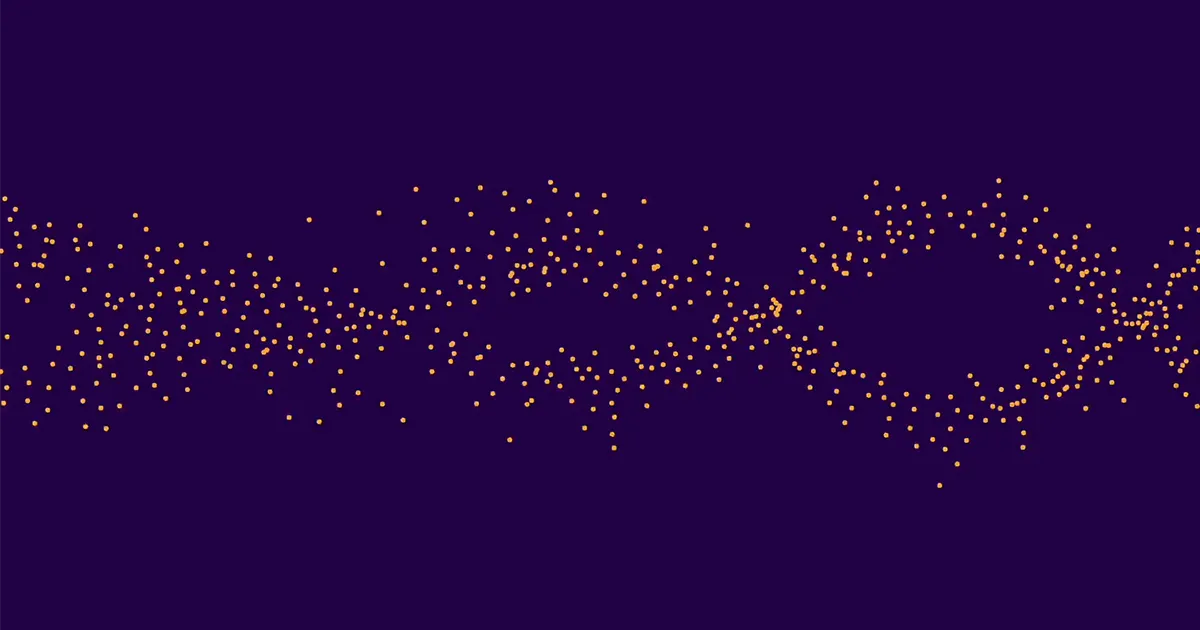
Detta uppgick till cirka 10,000 0 kurvor totalt. Ungefär hälften av dessa hade rang 1 och hälften rang XNUMX. (Högre rang är ytterst sällsynta.) Han tog sedan ett medelvärde av värdena för a_p för alla rang 0-kurvor, separat medelvärde a_p för alla rank 1-kurvorna och plottade resultaten. De två uppsättningarna av prickar bildade två distinkta, lätt urskiljbara vågor. Det var därför som maskininlärningsklassificerarna hade kunnat fastställa rangen av särskilda kurvor korrekt.

"Först kände jag mig bara glad över att jag hade slutfört uppdraget," sa Pozdnyakov. "Men Kyu-Hwan insåg direkt att det här mönstret var överraskande, och det var då det blev riktigt spännande."

Lee och Oliver var hänförda. "Alexey visade oss bilden, och jag sa att det ser ut som det där som fåglar gör," sa Oliver. "Och sedan slog Kyu-Hwan upp det och sa att det kallas ett sorl, och sedan sa Yang att vi skulle ringa tidningen"Murmurer av elliptiska kurvor'.”

De laddade upp sin uppsats i april 2022 och vidarebefordrade den till en handfull andra matematiker och förväntade sig nervöst att få veta att deras så kallade "upptäckt" var välkänd. Oliver sa att förhållandet var så synligt att det borde ha uppmärksammats för länge sedan.

Nästan omedelbart väckte förtrycket intresse, särskilt från Andrew Sutherland, en forskare vid MIT som är en av chefredaktörerna för LMFDB. Sutherland insåg att 3 miljoner elliptiska kurvor inte var tillräckligt för hans syften. Han ville titta på mycket större ledningsområden för att se hur robusta sorlet var. Han hämtade data från ett annat enormt förråd med cirka 150 miljoner elliptiska kurvor. Fortfarande missnöjd drog han sedan in data från ett annat förråd med 300 miljoner kurvor.

"Men även de var inte tillräckligt, så jag beräknade faktiskt en ny datamängd på över en miljard elliptiska kurvor, och det var vad jag använde för att beräkna de riktigt högupplösta bilderna," sa Sutherland. Mumlen visade sig om han i genomsnitt hade över 15,000 XNUMX elliptiska kurvor åt gången eller en miljon åt gången. Formen förblev densamma även när han tittade på kurvorna över större och större primtal, ett fenomen som kallas skalinvarians. Sutherland insåg också att mumling inte är unikt för elliptiska kurvor, utan också förekommer mer generellt L-funktioner. Han skrev ett brev som sammanfattar hans upptäckter och skickade den till Sarnak och Michael Rubinstein vid University of Waterloo.

"Om det finns en känd förklaring till det förväntar jag mig att du kommer att veta det", skrev Sutherland.

Det gjorde de inte.

Förklara mönstret

Lee, He och Oliver anordnade en workshop om muml i augusti 2023 vid Brown Universitys Institute for Computational and Experimental Research in Mathematics (ICERM). Sarnak och Rubinstein kom, liksom Sarnaks elev Nina Zubrilina.

Zubrilina presenterade sin forskning om murmurmönster i modulära former, speciella komplexa funktioner som, liksom elliptiska kurvor, har associerats L-funktioner. I modulära former med stora ledare konvergerar sorlet till en skarpt definierad kurva, snarare än att bilda ett urskiljbart men spritt mönster. I ett papper postat den 11 oktober 2023 bevisade Zubrilina att den här typen av sorl följer en explicit formel hon upptäckte.

”Ninas stora prestation är att hon har gett en formel för detta; Jag kallar det Zubrilinas formel för mumlande densitet, sa Sarnak. "Med mycket sofistikerad matematik har hon bevisat en exakt formel som passar data perfekt."

Hennes formel är komplicerad, men Sarnak hyllar den som en viktig ny typ av funktion, jämförbar med de luftiga funktionerna som definierar lösningar på differentialekvationer som används i en mängd olika sammanhang inom fysiken, allt från optik till kvantmekanik.

Även om Zubrilinas formel var den första, har andra följt efter. "Varje vecka nu kommer det ut ett nytt papper," sa Sarnak, "främst med hjälp av Zubrilinas verktyg, som förklarar andra aspekter av mumlande."

Jonathan Bober, Andrew Booker och Min lee vid University of Bristol, tillsammans med David Lowry-Duda av ICERM, bevisade förekomsten av en annan typ av murmur i modulära former i ännu en oktobertidning. Och Kyu-Hwan Lee, Oliver och Pozdnyakov bevisat existensen av muml i föremål som kallas Dirichlet-karaktärer som är nära besläktade med L-funktioner.

Sutherland var imponerad av den betydande dos tur som hade lett till upptäckten av muml. Om den elliptiska kurvan inte hade beställts av konduktören, skulle mumlet ha försvunnit. "De hade turen att ta data från LMFDB, som kom försorterade enligt konduktören," sa han. "Det är det som relaterar en elliptisk kurva till motsvarande modulära form, men det är inte alls uppenbart. ... Två kurvor vars ekvationer ser väldigt lika ut kan ha väldigt olika ledare.” Till exempel noterade Sutherland det y² = x³ - 11x + 6 har ledare 17, men vänder minustecknet till ett plustecken, y² = x³ + 11x + 6 har ledare 100,736 XNUMX.

Redan då hittades mumlen bara på grund av Pozdnyakovs oerfarenhet. "Jag tror inte att vi skulle ha hittat det utan honom", sa Oliver, "eftersom experterna traditionellt normaliserar a_p att ha absolut värde 1. Men han normaliserade dem inte ... så svängningarna var väldigt stora och synliga.”

De statistiska mönstren som AI-algoritmer använder för att sortera elliptiska kurvor efter rang finns i ett parameterutrymme med hundratals dimensioner - för många för att människor ska kunna sortera igenom i sina sinnen, än mindre visualisera, noterade Oliver. Men även om maskininlärning hittade de dolda svängningarna, "först senare förstod vi att de var sorlen."

Redaktörens anmärkning: Andrew Sutherland, Kyu-Hwan Lee och databasen L-functions and modular forms (LMFDB) har alla fått finansiering från Simons Foundation, som också finansierar denna redaktionellt oberoende publikation. Simons Foundations finansieringsbeslut har inget inflytande på vår täckning. Mer information finns tillgänglig här..